【例3-8】水自直径为d的圆管中以速度V垂直喷向竖直放置的平板CD,如图3-25所示。试求平板所受到的水流冲击力R。
解:这是一个射流冲击平板的问题,不要求求解射流流域内部的流动细节,也无须求解平板上的压强分布,只需求解平板所受的冲击力,故是一个动量定理应用的典型问题。
第1步选取控制体。
选取以ABCDEFA所围区域为控制体,并选取沿射流轴向向右方向为x轴正方向。
第2步对控制体内的流体进行受力分析。
控制体内的流体所受的作用力如下:
(1)通过各个控制面作用在流体上的大气压力,这部分力处于平衡状态,合力为0。
(2)控制体内的流体所受重力,在x轴上投影为0。
(3)设平板对控制体内流体的作用力为R,假设为理想流体,故R方向垂直于平板,沿x反方向。
第3步进行动量分析。
(1)AB、EF为流线,没有质量的流入与流出,当然也就没有动量的交换。
(2)CD为固壁,当然也就没有动量的交换。
(3)经过BC、DE流出的动量与x轴垂直,在x轴上的分量为0。
(4)经AF流入的速度为V,单位时间流入的动量为ρQV。
第4步列动量方程并求解。
沿x方向列动量方程,有
![]()
解得平板所受的水流冲击力为
注:这也是靶式流量计的工作原理,测得平板的受力R,即可反算出喷水流量Q。
问题研究:水流冲击平板的数值模拟计算(见第10章)
【例3-9】水自直径为d的管中以速度V冲击一倾斜的平板,如图3-26所示,已知平板与射流轴线夹角为β,设水流为理想流体,不计重力影响,试求平板所受到的水流冲击力R以及流量Q1和Q2。
解:这是一个利用动量定理进行求解的典型问题,选取Oxy坐标,如图3-26所示。
第1步选取控制体:选取ABCDEFA所围区域为控制体。
第2步对控制体内的流体进行受力分析。
(1)通过各个控制面作用在流体上的大气压力,这部分力处于平衡状态,合力为0。
(2)控制体内的流体所受重力不计。(相比射流冲击力而言,重力往往可以忽略)
(3)平板对流体的作用力为R,假设为理想流体,故R方向垂直于平板。
第3步进行动量分析。
(1)AB、EF为流线,没有质量的流入与流出,当然也就没有动量的交换。
(2)CD为固壁,当然也就没有动量的交换。

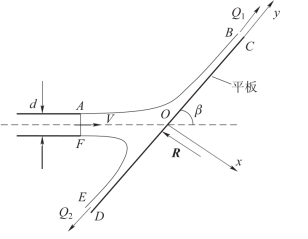
图3-26 水流冲击倾斜的平板
![]()
再由连续性方程,有
![]()
联解式(b)和式(c),最后得到
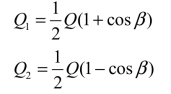
【例3-10】水自直径为d的管中以速度V垂直喷向相距为L的半圆弧板如图3-27所示,设水为理想流体,不计重力,试求半圆弧板所受到的水流冲击力R。
解:用动量定理求解此问题。
第1步选取控制体。
选取以ABCDEFA所围区域为控制体,并选取沿射流轴向向右方向为x轴正方向。
第2步对控制体内的流体进行受力分析。
控制体内的流体所受的作用力如下:
(1)通过各个控制面作用在流体上的大气压力处于平衡状态,合力为0。
(2)不计控制体内的流体所受到的重力影响。
(3)板对流体的作用力为R,假设为理想流体,故R的方向沿x轴反方向。
第3步进行动量分析。
(1)AB、EF为流线,没有质量的流入与流出,当然也就没有动量的交换。
(2)CD为固壁,当然也就没有动量的交换。
(3)由于不计重力影响,由伯努利方程,有V1 =V2 =V。经过BC和DE流出的动量大小共为ρQV,方向与x轴相反。
经AF流入的速度为V,单位时间流入的动量大小为ρQV。(https://www.xing528.com)
第4步列动量方程并求解
![]()
沿x方向列动量方程,有解得平板所受的水流冲击力为
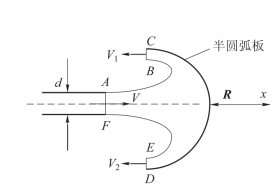
图3-27 水流冲击半圆弧板
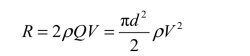
【例3-11】两个大水箱如图3-28所示。大水箱A距液面下H处接一个直径为d的管子,水自管中喷出后冲击水箱B壁面处的平板,使平板将水箱B壁面上直径为d的小孔挡住没有泄漏。现自水箱B右下的小孔向水箱内缓慢注水,问水箱B内液面高h为多大时才能把挡板推开,并使水箱B的水泄漏出来。假设大水箱A的液面高H不变,不计一切流动损失。
解:这是一个伯努利方程与动量定理以及静力学联合求解的例子。首先不妨猜一下,h与H的关系,大于、小于或相等?然后进行计算求解。
![]()
水流冲击平板的力为
![]()
水箱B中液体处于静止状态,对平板的静压力为
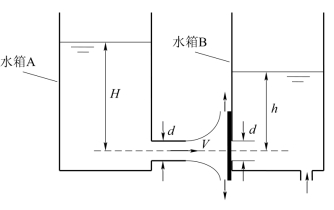
图3-28 例3-11用图
![]()
当P =R时,平板处于即将打开状态,此时有
![]()
这个结果你猜到了吗?为什么呢?

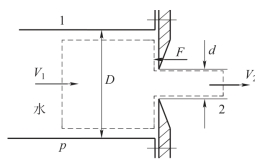
图3-29 例3-12用图
解:
由连续性方程,求得出流速度
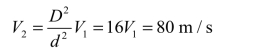
自1截面到2截面列伯努利方程,考虑到2截面压强为大气压,相对压强为0,有
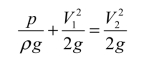
解得1截面处压强为
![]()
取控制体如图3-29中虚线所围区域,沿轴向列动量方程如下:
![]()
将流量
![]()
代入,最后得到水流作用在闸门上的力为
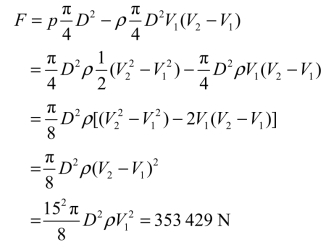
【例3-13】上下圆盘半径均为R=100 mm,相距为h=1 mm。上圆盘连接一个直径d=50 mm的管道,水流在管道中以速度V=1 m/s流动,并冲击下面的圆盘,如图3-30所示,假设为理想流体,不计一切流动损失,不计重力影响,试求下面圆盘所受到的水流作用力。
解:

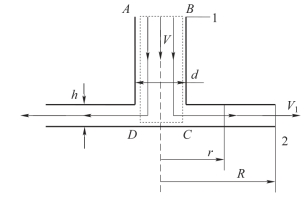
图3-30 例3-13用图
自管道截面1到圆盘外缘截面2列伯努利方程,设1截面处的压强为p0,并设大圆盘的外缘通大气,则有
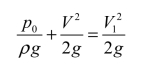
得到管道入口处压强为
![]()
大圆盘的受力需分两步来进行计算,第一步用动量定理计算DC部分(底盘上与管道截面面积相等的一部分区域)的水流冲击力;第二步用伯努利方程计算半径大于d/2那部分区域的压强分布,并积分得到这一区域的受力。将两部分合起来,就是整个圆盘的受力。
选取图中虚线所围ABCDA部分为控制体,设圆盘对这一部分流体的作用力为F1,方向向上。考虑到流出控制体的动量沿管道轴线的投影为0,沿管道轴线方向列动量方程,有

对圆盘半径大于d/2部分的受力进行积分,得到
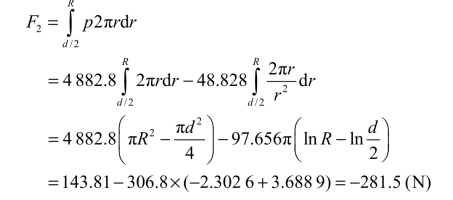
这个力为负数,为什么?
将以上两个力相加,最后得到圆盘所受的力为
![]()
计算结果说明底盘受到向上的吸力。
讨论:若使圆盘所受合力为零,条件是什么?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




