【摘要】:对于不可压缩流体,密度ρ为常数,对式进行积分,得到这就是著名的伯努利方程,是由瑞士科学家伯努利于1738年首先提出的。注意1:伯努利方程的使用条件如下:流体为理想流体。注意2:伯努利方程表示,沿一条流线单位质量流体的位能、压能和动能之和为常数。这是机械能守恒在流体力学中的体现,也是伯努利方程的物理意义。
对于不可压缩流体,密度ρ为常数,对式(3-20)进行积分,得到

这就是著名的伯努利方程,是由瑞士科学家伯努利(Daniel Bernoulli)于1738年首先提出的。
理想流体的伯努利方程表明,在如图3-12所示的同一条流线上的任意两点1、2之间,应满足
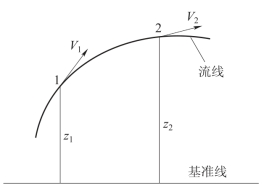
图3-12 沿流线上机械能守恒
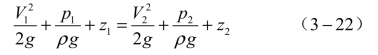
即单位重量流体的机械能是守恒的(总水头是不变的),式(3-21)的物理意义就是机械能守恒,故又称为能量方程。
注意1:伯努利方程的使用条件如下:
(1)流体为理想流体。
(2)流动为定常流动。
(3)流体是不可压缩的。(https://www.xing528.com)
(4)只有重力场,质量力只有重力。
(5)沿一条流线。
沿不同的流线,常数的值一般是不相同的。
注意2:伯努利方程表示,沿一条流线单位质量流体的位能、压能和动能之和为常数。这是机械能守恒在流体力学中的体现,也是伯努利方程的物理意义。
注意3:对于水流而言,如果某点的压强低于水的汽化压强,则会产生气泡,发生汽化现象,此时方程(3-21)就不再适用了。
有几个常用的名称介绍如下:

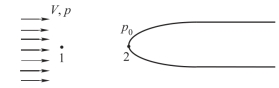
图3-13 静压、动压和总压
如果流体以速度V绕流一个固定的物体,如图3-13所示,在1点处压强(静压)为p,速度为V;2点处的速度为0,为驻点,压强(总压)为p0,则有
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




