半导体电学特性：电阻率随温度线性变化的金属

1.eV

1eV（电子伏特）是1个单位电荷通过1V的电位差所获得的能量。1个单位电荷通过100V电位差所获得的能量为100eV，两个单位电荷通过100V电位差所获得的能量为200eV。

2.欧姆接触

金属与半导体间没有整流（把交流电变为直流电）作用的接触称为欧姆接触。实际上的欧姆接触几乎都是采用金属-N＋N半导体或金属-P＋P半导体的形式制成的。在这种接触中，金属与重掺杂的半导体区接触，接触界面附近存在大量的复合中心，而且电流通过接触界面时的压降也往往小到不计。制造欧姆接触有两种方法：

1）如果金属本身是半导体的施主或受主元件，而且在半导体中有高的固溶度，就用合金法直接在半导体中形成金属-N＋区或金属-P＋区。如果金属本身不是施主或受主元素，可在金属中掺入施主或受主元素，用合金法形成欧姆接触。

2）在半导体中先扩散形成重掺杂区，然后使金属与半导体接触，形成欧姆接触。

3.纯度表达

纯度一般按多少个9来表达。5N，即5个9，表示纯度为99.999％，N为英文nine的第一个字母。有时用电阻率来表达，材料的电阻率越高，其纯度越高。

4.电阻率

1）电阻率是表示物质电阻特性的物理量。长为1m、横截面积为1mm²的导线20℃时的电阻，称为该材料的电阻率。其计算公式为

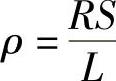
式中ρ——电阻率（Ω·m）；

S——横截面积（mm²）；

R——电阻（Ω）；

L——导线的长度（m）。

2）电阻率不仅与导体的材料有关，还和导体的温度有关，在温度变化不大时，几乎所有金属的电阻率随温度作线性变化。其公式为

式中ρ₀——0℃时的电阻率；

α——电阻率温度系数；

t——摄氏温度。

3）电阻率和电阻是两个不同的概念，电阻率是反应物质对电流阻碍的属性，电阻是反应物体对电流的阻碍作用。

4）电阻率除以金属膜的厚度即是方块电阻，电阻大小为方块电阻乘以金属块的长与宽之比。

5.电导率

电导率用来表示物质中电流流动的难易程度，是物质固有的物理量。电导率σ与电阻率ρ之间是互为倒数的关系，即

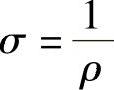
电导率的单位是S／m或Ω^－1·m^－1，S读作西（门子），电导（S）与电阻（Ω）互为倒数关系，S可以用电压和电流单位表示，即1S=1A／V。

对于半导体材料，由于电子和空穴同时导电，存在两种载流子，其电导率表示为

σ=neμ₁＋αeμ₂式中n、α——电子、空穴的浓度（原子／cm³）；

μ1、μ2——电子、空穴的迁移率[cm²／（V·s）］；

e——载流子电量。

室温下的电导率：导体约在10⁵S／m以上，半导体在10^－10～10⁵S／m，绝缘体小于10^－10 S／m。

6.势阱

阱是指捕野兽用的陷坑。粒子在某力场中运动，从势能函数曲线可知在空间的某一有限范围内势能最小，形如陷阱，称为势阱（Potential Well），就是电子的势能图像类似一个波的形状，那么当电子处于波谷时，就好像处在一口井里，比较稳定，很难跑出来。

7.量子阱（QW）

量子阱（QW）是指由两种不同的半导体材料相间排列形成的、具有明显量子限制效应的电子或空穴的势阱。量子阱的最基本特征是：量子阱中因为有源层的厚度仅在电子平均自由程内，阱壁具有很强的限制作用，使得载流子只在与阱壁平行的平面内具有二维自由度，在垂直方向使得导带和价带分裂成子带。

在由两种不同半导体材料薄层交替生长形成的多层结构中，如果势垒层足够厚，以致相邻势阱之间载流子波函数之间耦合很小，则多层结构将形成许多分离的量子阱，称为多量子阱（MQW）。量子阱中的电子态、声子态和其他元激发过程以及它们之间的相互作用，与三维体状材料中的情况有很大差别。在具有二维自由度的量子阱中，电子和空穴的态密度与能量的关系为台阶形状，而不是像三维体材料那样的抛物线形状。

量子阱的制备通常是通过将一种材料夹在两种材料（通常是宽禁带材料）之间而形成的，比如两层砷化铝之间夹着砷化镓，一般这种材料可以通过MBE（分子束）外延或者MOCVD（金属有机化学气相沉积）的方法来制备。

8.隧道结

在势垒一边平动的粒子，当动能小于势垒高度时，按经典力学，粒子是不可能穿过势垒的。对于微观粒子，量子力学却证明它仍有一定的概率穿过势垒，实际也正是如此，这种现象称为隧道效应。对于谐振子，按经典力学，由核间距所决定的位能绝不可能超过总能量。量子力学却证明这种核间距仍有一定的概率存在，此现象也是一种隧道效应。在两层金属导体之间夹一薄绝缘层，就构成一个电子的隧道结。

9.方块电阻

一个均匀导体的电阻R正比于导体的长度L，反比于导体的截面积S。如果这个导体是一个宽为W、厚度为d的薄层，则

(www.xing528.com)

薄层电阻与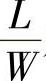成正比，比例系数为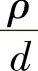，这个比例系数就叫方块电阻，用R_s表示，则有

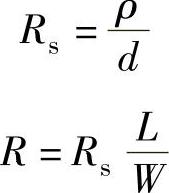
R_s的单位为欧姆，通常用符号Ω／▯表示，以区别于其他电阻，“▯”是方块符号。从上式可以看出，当L=W时有R=R_s，这时R_s表示一个正方形薄层电阻，它与正方形边长无关，这就是取名方块电阻的原因。

10.测量方块电阻（薄膜电阻）

一般用四探针法测量方块电阻。四探针是四根彼此等距离为S的钨丝探针，其针尖保持在一条直线上，且以等量压力压在硅片（薄膜）的表面。一对外探针为电流探针，由稳压电源供电，在薄层中通过一定量的电流（I），相应有一定的电场分布。一对内探针为电位探针，测定距离为S的两点间的电位差（U）。如果薄膜的长度、宽度比探针间距大得多，则方块电阻的表达式为

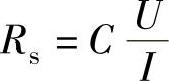
式中C——修正系数，由被测样品的长度、宽度、厚度及探针间距S来确定，C可以查表

得到；

R_s——方块电阻。

11.活化

活化又称为激发（Excitation），是指粒子（如原子或离子）从外界获得足够能量后，其电子由较低的基态能级跃迁到较高能级的过程。一个分子是否为活化分子，根据不同的速率理论及反应，其标准不同。如碰撞理论中，分子能量ε＞ε₀（阈能）的分子为活化分子，活化分子也不一定是过渡态，如单分子理论中的赋能分子。另外，活化也常指某一物质从其无活性状态转变为具有活性状态的过程，其中也包括生物细胞或孢子在休眠后进入重新生长状态。例如金属催化剂的活化，即为从其氧化物状态转变为金属状态的过程；生物孢子在适宜的生长环境中再次繁殖。活化方式有碰撞传能活化及光活化等多种方式。

12.活化的能量

非活化分子转变为活化分子需要吸收能量。温度对反应速率有显著影响。在多数情况下，其定量规律可由阿伦尼乌斯公式来描述：

式中κ——反应的速率系（常）数；

E、A——分别称为活化能和指前因子，是化学动力学中极重要的两个参数；

R——摩尔气体常数；

T——活化后热力学温度。

对于更为复杂的描述κ与T的关系式，活化能E定义为

在反应中，并不是反应物分子的每一次碰撞都能发生反应。S.A.阿伦尼乌斯认为，只有活化分子之间的碰撞才能发生反应，而活化分子的平均能量与反应物分子平均能量的差值即为活化能。近代反应速率理论进一步指出，两个分子发生反应时必须经过一个过渡态——活化络合物，过渡态具有比反应物分子和产物分子都要高的势能，互撞的反应物分子必须具有较高的能量（足以克服反应势能垒），才能形成过渡态而发生反应，此即活化能的本质。式（3-3）可写成对数形式

根据式（3-5），由实验测出不同温度下的κ值，并将lnκ对1／T作图，即可由所得直线的斜率求出E值。也可将由实验归纳出的κ与T的经验关系式直接代入式（3-4）求得E值。

对于复合反应，由上述实验方法求出的E值只是表观值，没有实际的物理意义。

13.功函数

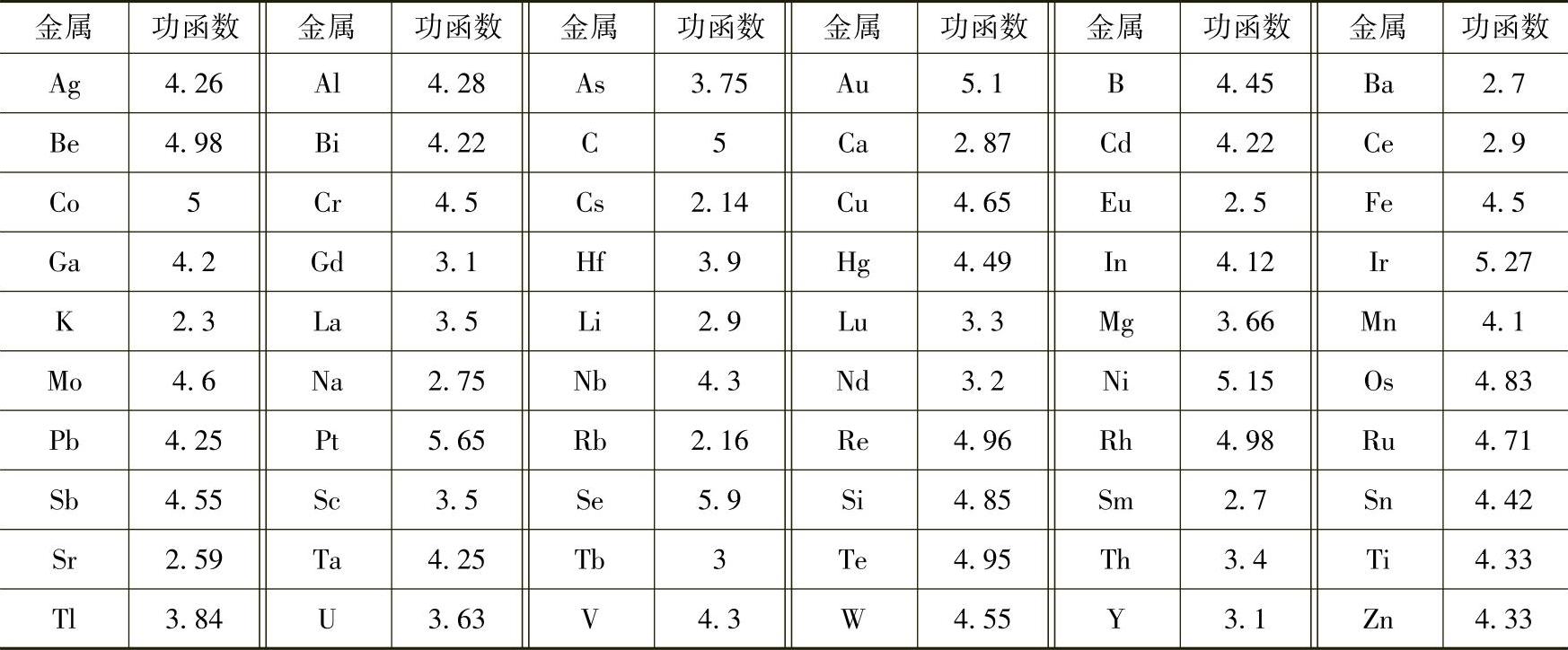
功函数（Work Function）又称为功函、逸出功，在固体物理中被定义为，把一个电子从固体内部刚刚移到此物体表面所需的最少的能量。功函数的大小大概是金属自由原子电离能的二分之一。表3-7为金属的功函数。

（1）光电功函数 功函数是从某种金属释放电子所必须给予的最小能量。在光电效应中，如果一个拥有的能量比功函数大的光子被照射到金属上，则光电发射将会发生，且任何超出的能量将以动能形式给予电子。

光电功函数为φ=hf

光电功函数为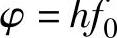

式中h——普朗克常数；

f₀——能产生光电发射光子的最小（阈值）频率。

当电子获得能量时，它从一个能级以“量子跃迁”的方式跳到另一个能级。这一过程称为电子的激发，其中较高能级称为激发态，而较低能级称为基态。

表3-7 金属的功函数（单位：eV）

（2）热功函数 功函数在热发射理论中也同等重要。这里电子从热而非光子中获得能量。在这种情况下，电子从加热的充满负电的真空管灯丝逃逸，功函数可被称为热功函数。钨是真空管中常见的金属元素，它的热功函数大约是4.5eV。

热发射要求有灯丝加热电流（I_f），来保持2000～2700K的温度。一旦达到灯丝电流的饱和态，则灯丝电流的小改变不再影响电子束电流。电子枪被提供一个非常靠近克服功函数（W）所需的灯丝电流（Goldstein，2003）。热功函数取决于晶体取向，而且趋向于对于开放晶格的金属更小，对于原子紧密堆积的金属更大，范围大概是1.5～6eV；某种程度上稠密晶面比开放晶格金属更高。

在电子学里，功函数对设计肖特基二极管或发光二极管中金属-半导体结以及真空管非常重要。

（3）测量 很多基于不同物理效应的技术被发展出来来测量样品的电学功函数。

第一类方法利用样品由光吸收（光发射）所引发的电子发射，通过高温（热发射）或者电场（场发射），以及使用电子隧穿效应来测量。

第二类方法是相对测量方法，利用样品与参照电极的接触势差。实验上，是使用二极管的阴极电流或者样品与参照物之间，由人工改变的两者间电容导致的位移电流等方法（开尔文探测、开尔文探测力显微镜）来测量的。