预裂爆破中的线装药密度计算与应用

1. 不同的计算方法的观点

对预裂装药密度，本节将列出国内学者不同的观点和方法如下：

① 美国尼亚加拉水电站预裂爆破总结中提出过一个方法[2]，此法是在保证不压坏孔壁的情况下，决定每米炮眼长度的药卷长度（即线装药密度），然后校核在此药量下两孔间距在某一数值时产生的拉应力是否大于岩石抗拉强度。校核通过即表示参数可以使用。

② 苏联阿·阿·阿费柯和伯·斯·艾里斯托夫在水工建设中的轮廓爆破一书中提出了另一个计算方法[42]。

文献[1]指出：以上两种方法都是以爆炸应力波的动力作为主要依据进行公式推导的，对于爆生气体作用没有考虑。

以上两个公式推导本身还不够严谨、完善，某些重要因素尚未包括在内。加之施工和地质条件复杂多变，公式中的因素很难正确选定。它们只能定性地反映主要参数间的关系和函数形式。

③ 我国原水利电力学院董振华、周祖仁、舒大强等[6]提出的线装药密度。他们提出不致使孔壁压坏的最大装药量称之为允许装药量，产生初始径向裂缝的最小装药量称为临界药量。

2. 实践中常用的炮孔装药的计算方法

在预裂爆破工作实践中，常用线装药密度Q线来表示炮孔装药量。当计算的体积装药密度Δ允以克/厘米3为单位时，相应的线装药密度Q线将为：

当环向不耦合系数η =rc/rb值确定后，单位孔深的装药长度Lh将为：

3. 断裂判据

原武汉水利电力学院朱传云[34]按照线弹性断裂力学原理，在不考虑岩石原始裂纹对爆破应力强度因子影响的条件下提出了控制预裂爆破的断裂判据，建立了预裂爆破的线装药密度计算公式（在应用准静态气体荷载对炮孔壁作用的前提下）。

（1）岩石的爆破断裂判据。

根据线弹性断裂理论，在岩石中进行预裂爆破时，预裂缝的扩展可近似认为属于Ⅰ型裂纹，如图12-5 所示，因此，爆破时欲使相邻炮孔之间能形成预裂缝并发生脆性断裂，则应满足以下的条件：

式中 KI—— 作用到炮孔壁上的爆炸荷载产生的应力强度因子（N/cm3/2）；

KIC—— 岩石的断裂韧度值（N/cm3/2）。

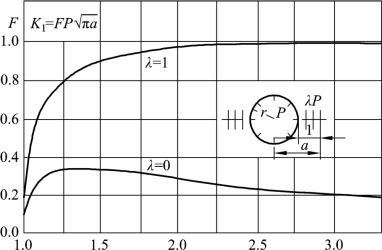
图12-5　承受内压圆孔当两边有裂纹时应力强度因子曲线

当实施预裂爆破时，如果单耗药量能满足式（12-3）的要求，且炮孔间距适当，则在相邻炮孔连心线上能产生裂缝，并在失稳情况下向相邻炮孔延伸，最终使孔间裂缝贯通。

式（12-3）中的KI可以根据图12-5 的模型和式（12-4）算出。

式中 F—— 断裂影响系数；

P —— 作用到炮孔壁上的爆炸荷载；

a —— 初始裂纹长度，等于图12-5 中原始裂纹长度τ 与炮孔半径r 之和。

由上所述，炮孔周围的原始裂纹长度不是一个定值，由于它的随机性，将会给爆破参数的计算带来一些困难。作为近似处理，可令原始裂纹长度τ 趋于零，按图12-5 中λ = 0时的曲线，可查出F =0.1，则作用到炮孔壁上的临界压力Pc可用下式算出，即：

（2）文献[34]根据准静态气体对孔壁作用推导出的线装药密度计算公式。

由于爆生气体对预裂缝的形成起主要作用这一理论解释已被工程界广泛接受，因此，本节在考虑准静态气体荷载对炮孔壁作用的前提下，对预裂爆破的有关参数作出推导，并给出结论。(www.xing528.com)

① 作用到炮孔壁上的准静态爆炸气体荷载。由凝聚性炸药爆轰理论可知，炸药爆炸时，爆炸气体的初始平均压力为

考虑到量纲的一致性，则

式中 PH—— 爆炸气体的初始平均压力（MPa）；

k —— 炸药的等熵指数；

ρ0—— 炸药的密度，其中δ 为炸药容重，g 为重力加速度；

υ—— 炸药的爆炸传播速度（m/s）。

若设爆生气体膨胀至孔壁时的压力为 P0，则对应于 P0、临界压力 PI及 PH的气体体积，分别为V0、VI和VH，根据爆生气体状态方程，则有

式中 γ —— 气体的绝热膨胀指数，取值为1.4；

其他符号意义同前。

令Δ 为炮孔的体积装药密度（即炮孔单位积的装药量），则有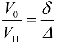，将其代入式（12-8）中，就会算出炸药爆炸时作用到炮孔壁上的爆炸气体压力为：

按照有关文献所提供的资料，在使用2 号岩石硝胺炸药时，k 近似取值1.84，爆破速度为3.6 km/s，炸药密度为1.0 g/cm3；所以，当使用2 号硝胺炸药时，作用到炮孔壁上的爆炸气体压力Pc=12 908Δ1.4。

② 临界线装药密度。

在预裂爆破中，人们习惯采用线装药密度Q线（g/m）来表示爆破的装药参数，则有（D 为炮孔直径），代入Pc=12 908Δ1.4中，则有：

根据式（12-5）与式（12-10）相等的条件，则可得到预裂爆破的临界线装药密度Q线临为：

③ 计算线装药密度。

按照式（12-5）与式（12-10）算出的爆炸荷载对炮孔壁的压力只是起码条件，虽然这个荷载有可能使预裂向相邻炮孔失稳扩展，但当来自岩体的阻力超过某个值后，裂缝的扩展就会终止，而不能贯通相邻炮孔。为了使相邻炮孔间的裂缝能贯通，故设预裂爆破的炮孔间距为a，则每个炮孔的裂缝应向相邻炮孔延伸的距离即为，此时，爆炸荷载应为 P0′可按下式计算：

由式（12-10）与式（12-12）相等的条件，即可得出：

或

几种常见岩石的断裂韧变值见表12-1。

表12-1　几种常见岩石的断裂韧变值