爆炸能量分布及其计算方法

计算时爆炸过程中各项所做的功等于其所消耗的能量，它们与炸药总能量的比值为其所消耗的能量占总能量的百分比。（计算方详见参考文献[19]736～738 页或[24][25]）

1. 冲击波能量的消耗

冲击波能量的消耗等于冲击波对岩石所做的功，在爆腔扩张过程中冲击波所做的功为[19]

将岩石冲击波峰值压力的衰减公式代入式（6-10）积分得

2. 应力波产生径向裂隙做功

（1）粉碎区外，冲击波衰减为应力波引起岩石切向受拉形成裂隙区。

（2）卢文波、陶振宇先生的资料表明：采用平面楔形裂纹模型比较合适。同时，根据岩石断裂力学原理，考虑炮孔柱状装药爆破可以看作平面应变问题[19]可得能量释放率K1为应力强度因子。

（3）由于裂隙长度扩展 Δd 时，其裂隙端部的应力强度应可以认为相等。因此，可求得裂隙在扩展过程中切向应力所做的功为：

式中： n1—— 径向裂纹的系数。

（4）根据资料[19]，主导裂隙将从裂隙群中突出发展，由试验所得主导为4～12 条，计算取 n1= 8。对于张开型裂纹，在其延长线上，即有Q= 0，则裂隙端的切向应力与应力强度因子的关系为：，式中 rj为炮孔中心到裂隙端部的距离，将上式代入式（6-12）后积分整理得[19]：

3. 应力波引起的弹性变形

裂隙区外，应力波只能引起弹性变形。在计算弹性变消耗的能量时，根据宗琦、杨吕俊提供的资料[25]，单位体积内岩石的弹性变形能为：

由此，应力波、冲击波引起岩石弹性变形所做的功为：

4. 爆生气体的扩腔

（1）紧随冲击波之后，爆生气体膨胀继续扩大爆腔，当腔内爆生气体压力P 等于围岩压力 Ps时[19]，爆扩过程结束，爆扩过程的围岩压力[27]为：

式中： Patm—— 大气压力；

σs—— 多向应力条件下岩石极限抗压强度，

σs=(ρm/ σc)1/4σc

rm—— 岩石的重度；

W —— 抵抗线。

（2）由于 Patm、 rmW 与 σs相比可以忽略不计[19]，即 Ps= σs。

（3）为了简化计算，忽略气体孔口和裂隙泄漏，对于绝热膨胀，在爆腔内的膨胀规律宗琦先生[24]提出：

式中：P—— 爆生气体膨胀过程的瞬时压力；

P0—— 膨胀开始的爆生气体压力，耦合装药时其值等于平均爆轰压力，即

P0=ρ0D2/(2 +2λ )(www.xing528.com)

r2—— 与P 相对应的爆腔瞬时半径；

rk—— 爆生气体由等熵绝热膨胀时的临界爆腔半径；

Pk—— 与 rk对应的临界压力。

（4）变换式（6-17）[19]可得爆生气体膨胀作用下的爆腔扩胀规律，即：

（5）以 Ps取代式（6-18）中的P [19]，便可得爆腔的最终半径

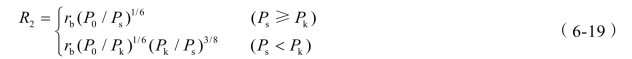
由此，可得爆生气体扩腔做功的计算式：

将式（6-18）代入式（6-20）积分得

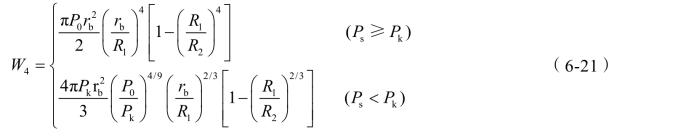
5. 爆生气体的驱裂

岩石的爆破破碎是应力波和准静态气体联合作用的结果。该理论认为：首先在应力波的作用下，在炮孔周围岩石中形成初始裂纹网，随后在爆生气体的准静态作用下，初始裂纹得到进一步延伸。考虑应力波超前传播的力学效应[19]，即对岩体的损伤，岩体的微观细观结构已有所改变。Kutter 和Fairhurst 认为[28]，应力波对岩体起着预荷载的作用。据此[19]，炮孔间准静态爆生气体驱动的平面楔形裂纹模型可由图6-1 所示。图中L（t）为爆生气体驱动的裂纹扩展总长度， L1( t )为爆生气体在裂纹中的贯入长度，而L0为应力波作用下产生的径向裂纹初始长度。

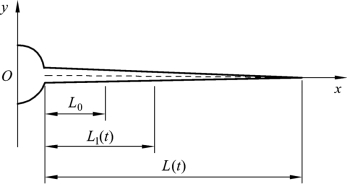
图6-1　爆生气体驱动裂纹扩展模型

（1）初始裂隙由冲击波所引起，随后在爆生气体的作用下进一步得到发展。作为工程计算时，当裂纹长度大于炮孔尺寸时，炮孔本身可作为裂纹的一部分，则有此模型下裂纹间断的应力强度因子[26,29,30]：

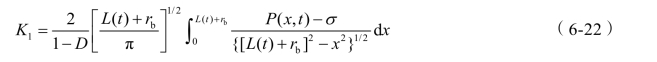
式中 P ( x, t )—— 沿裂纹长度方向的气体压力分布；

σ —— 垂直于裂纹面方向的远场应力；

D —— 裂纹尖端的损伤值，要获得岩体中每一点的损伤值，必须知道该点处的应变及应变率，文献[29]推荐了经验与理论相结合的办法，给出了应变波的简便求法。

法裂纹发展到最后一次止裂后，将不再扩展，设此时炮孔内压力为P，最终裂纹长度为L，则有[19]：

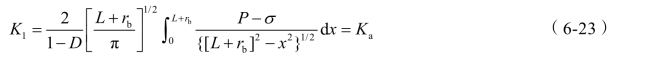
式中：Ka—— 岩石的止裂韧度。

（2）由上式可得裂纹在计损伤情况下应力波与准静态爆生气体压力作用下的最后裂纹长度，并可求得爆生气体对产生裂纹所做的功为：

6. 小 结

（1）计算时单位炸药能量为E0=πrb2ρ0Q ，Q 为炸药爆热，2#岩石硝铵炸药ρ0=1 000 kg/m3，v=3 600 m/s，爆热取3.76 MJ/kg。

（2）岩石物理参数见表6-3，计算结果见表6-4[19]。

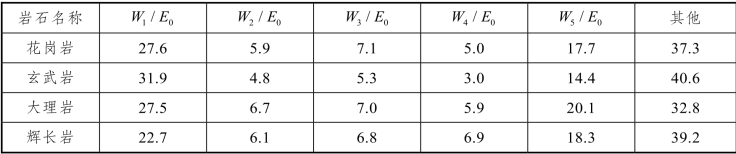
（3）冲击波做功消耗的能量约占爆炸总能量的40%，剩余爆生气体能量约占总能量的60%，其中用于扩腔和扩展主要裂隙的能量约占总能量的23%；剩余大约37%的能量中有小部分能量用于新增裂纹数目，而大部分损失掉了[19]。

表6-3　岩石的物理力学性质及其a，b 值[19]

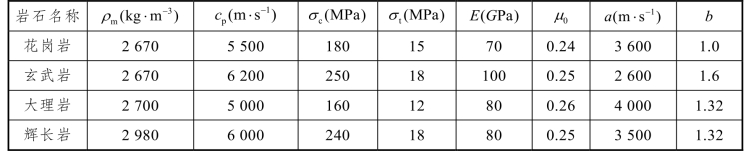
表6-4　爆炸能量分布计算结果[19]