应力波的反射特性探究

应力波在传播过程中，遇到自由面或节理、裂隙、断层等薄弱部位时都要发生波的反射和透射。当波遇到界面时，一部分波改变方向，但不透过界面，仍在入射介质中传播的现象称为反射。当波从一种介质穿过界面进入另一介质，入射线由于波速的改变，而改变传播方向的现象称为透射。

应力波向交界面垂直入射的情况，由于纵波是造成岩体破坏的主要因素，所以在此只讨论应力波为纵波时向交界面垂直入射的情况。

试看图4-22，当入射波由物体a 进入b 时，在界面上的点，既属于物体a，又属于物体b。从物体来看，这点同时受到一个入射的顺波和一个反射的逆波作用，利用波的叠加原理知：

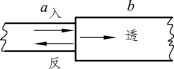
图4-22　波的透射和反射

从b 物体来看，界面上的点只受透射过来的顺波作用，即：

但界面上的同一点的应力和质点振动速度只能有一个，所以：

1. 应力波在传播中遇到自由面或介质界面时的入射、反射和透射

应力波在岩体中传播遇自由面或不同介质分面上的入射、反射和透射框架见图4-23 所示。

图4-23　应力波在岩体中传播遇自由面或不同介质分面上的反射、入射框架图

2. 应力波在自由面上的反射

应力波传播到自由面时均要发生反射，无论是纵波还是横波经过自由面反射后都要再度生成反射纵波和反射横波。

自由面上部为空气。与岩石密度相比，空气的密度可以认为是零。因此，应力波在自由面引起的位移不受限制，自由面上的应力也等于零。当应力波到达自由面时，将全面发生反射。

（1）纵波在自由面上的反射[14]。

当入射波为纵波时，纵波的入射角和反射纵波的反射角均等于α ，而反射横波生成的反射角为β ，如图4-24 所示。同时，反射横波的反射角β 与纵波的入射角α 之间，根据光学的斯涅尔（Snell）法则存在下列关系式：

图4-24　倾斜入射的纵波在自由面的反射

当纵波、横波在介质内部传播时，在介质中均要产生应力和应变。设通过自由面某点倾斜入射的纵波及其反射的纵波和横波引起的应力分别为iσ 、rσ 和rτ ，则三者存在下列关系式：

式中 R0—— 应力波的反射系数。

图4-25　纵波入射角α 与反射系数0R 之关系

纵波的入射角α 与反射系数 R0的关系如图4-25 所示。R0为负值，表示纵向应力波方向发生反向变化，压缩波变为拉伸波，拉伸波变为压缩波。当纵波倾斜入射时，自由面上质点的运动方向取决于3 个波引起质点位移的合成方向，如图4-26 所示。

式中 ∑u—— 3 个波引起的平行于自由面的质点位移合成值；

∑t—— 3 个波引起的垂直于自由面的质点位移合成值。

图4-26　三角波从自由面反射时的应力

纵波入射角α 与横波反射角β 的关系

纵波垂直入射自由面时，αi=0 ，此时与自由面成垂直方向的应力合力必然为零。其相位发生180°变化。即应力波若是以压缩波的形式传播，到达自由面时发生反射，压缩波变为拉伸波，并向介质中返回。此时，自由面附近的应力状态如图4-26 所示，设入射的三角波形为压缩波，从左向右传播，如图4-30（a）所示，则波在到达自由面之前，随着波的前进，介质承受压缩应力作用，当波到达自由面时立即发生反射。图4-31（b）表示三角波正在反射过程中，图4-30（c）表示波的反射过程已经结束。反射前后的波峰应力值和波形完全一样，但极性相反，由反射前的压缩波变为反射后的拉伸波，从原介质中返回。随着反射波的前进，介质从原来的压缩应力下被解除的同时，而承受拉伸应力。

（2）横波在自由面上的反射。

当入射波为横波时，在自由面上由入射波和反射波所引起的应力有下列关系：

（3）应力波在不同介质分界面上的反射和透射。

当应力波传到不同介质的分界面时，均要发生反射和透射，假设入射波为纵波（P）时，一般要激发4 种波，即反射纵波 Pr，反射横波 Sr，透射纵波 Pt和透射横波 St（图4-27）。(www.xing528.com)

图4-27　P 波由介质Ⅰ入射到介质Ⅱ中的示意图

波的反射部分和透射部分的应力波的形状变化取决于不同介质的边界条件。根据界面连续条件和牛顿第三定律，分界面两边质点运动速度相等，应力也相等。

式中的σ 和v 分别代表力和质点运动速度，下角标的字母i、r 和t 分别代表入射、反射和透射波。

假设传播的应力波为纵波，则

将式（4-114）代入式（4-113）得：

将式（4-112）与式（4-114）联立可得：

由式（4-118）可以看出，T 总为正，故透射波与入射波总是同号，F 的正负则取决于两种介质波阻抗的相对大小（图4-28）。

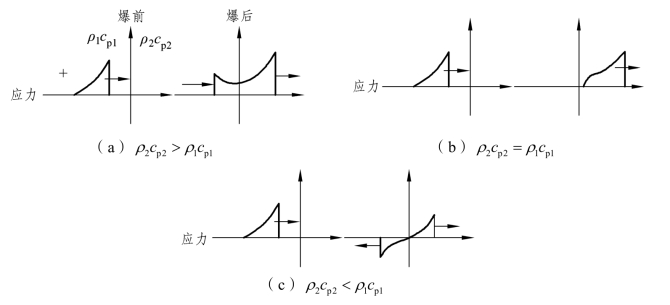
图4-28　应力波反射类型图

+ —压应力；- —拉应力

① 若ρ2cp2﹥ρ1cp1，则F﹥0，反射波和入射波同号，压缩波反射仍为压缩波，反向加载。

② 若ρ2cp2=ρ1cp1，则F=0，T=1，此时入射的应力波在通过交界面时没有发生波的反射，入射的应力波全部透射入第二种介质，就说明分界面两边的介质材料完全相同，无能量的损失。

③ 若ρ2cp2﹤ρ1cp1，则F﹤0，反射波和入射波异号，只要分界面能保持接触，不产生滑移，就既会出现透射的压缩波，也会出现反射的拉伸波。

④ 若ρ2cp2=0，类似于入射应力波到达自由面，则σt= 0，σr=-σi，在这种情况下入射波全部反射成拉伸波。

由于岩石的抗拉强度大大低于岩石的抗压强度，因此③、④两种情况都可能引起岩石破坏，尤其是后者，这充分说明了自由面在提高爆破效果方面的重要作用。

3. 岩石中的动应力场

爆破荷载为动荷载，在爆破荷载作用下，岩石中引起的应力状态表现为动的应力状态。它不仅随时间而变化，而且随距离远近而变化。

在爆炸应力波作用的大部分范围内，它是以压缩应力波的方式传播的，其引起的岩石应力状态可以近似地采用弹性理论来研究和解析。近代动应力的分析方法，就是按应力波的传播、衰减、反射和透射等一系列规律，计算应力场中各点在不同时刻的应力分布情况，以求得任何时刻的应力场及任意小单元体的应力状态随时间变化的规律。

当爆炸应力波从爆源向自由面倾斜入射时，在自由面附近某点岩石中产生的应力状态是由直达纵波、直达横波，纵波反射生成的反射纵波和反射横波、横波反射生成的反射纵波和反射横波的动应力状态叠加而成。为简化计算，下面仅考虑入射波是纵波的情况。如图4-29所示，设自由面方向为横轴，最小抵抗线方向为竖轴，O 点为炸药中心（即爆源），岩体中任一点A 的应力状态可作如下的分析：该点由入射直达纵波产生的应力为 σip，由反射纵波产生的应力为σrp，由反射横波产生的应力为 σrs，则A 点的应力为三者的合成，由合成应力引起的3 个主应力为 σ1、 σ2、 σ3。

图4-29　波到达A 点的应力分析

1—入射纵波；2—反射纵波；3—反射横波

当拉伸主应力 σ2出现极大值时，自由面附近岩体中各点的主应力 σ1和 σ2的方向如图4-30所示。这种应力分布方向对于解释爆破时岩体中发生的裂隙方向具有重要的意义。如果爆源附近有自由面时，自由面对应力极大值的变化产生很大的影响，一般来说在自由面附近所产生的压缩主应力极大值比无自由面时所产生的要大，爆源离自由面越近，拉伸主应力的增长越显著，这意味着自由面附近的岩石处于拉伸应力状态，易于被破坏。

A. H.哈努卡耶夫也得出类似的结果。图4-31 表示了入射波倾斜入射时，反射纵波（ Pr）和反射横波（ Sr）分别产生的主应力，包括拉应力、压应力和剪切应力。

由图4-31 可以看出：① 在反射纵波波阵面 Pr上，主应力方向为垂直于波阵面的方向和与波阵面相切的方向；在反射横波的波阵面上，主应力方向和波阵面成 45°夹角。② 在反射纵波的波阵面上，最小抵抗线处的应力值最大，距离最小抵抗线越远，应力值越小。在反射横波的波阵面上，最小抵抗线处的应力等于零。③ 地表附近岩层的“片落”主要靠反射纵波引起的拉应力作用。边缘地区的少部分岩石的断裂是剪切应力作用造成的，该剪切应力作用方向和纵波波阵面成 45°夹角，局部地方岩石的破坏是和反射横波波阵面平行的剪切应力造成的。

图4-30　当σ 达到最大值时r1和r2的作用方向

图4-31　在反射纵波和反射横波波阵面上的主应力的大小和方向

1—拉应力；2—压应力；3—剪应力

上述两个实例说明：① 自由面对应力极大值的变化有很大影响。② 自由面附近岩石主要靠反射纵波的拉伸应力破坏。

4. 岩石中的爆炸气体

如果将爆炸气体与冲击波相比较，从出现的时间讲，冲击波在前，爆炸气体在后。从对岩石的作用时间讲，冲击波作用时间短，爆炸气体作用时间长。尽管爆炸气体出现的时间晚，但是，由于它携带有巨大的能量和较长的作用时间，在破碎岩石中的作用是不可忽视的。

如果药包靠近自由面，孔壁岩石被高压冲击波压缩和粉碎，炮孔容积被扩大，被密封在炮孔中的爆炸气体以准静态压力作用在孔壁上。其力学分析方法是：首先由岩石的应力、应变、位移关系导出爆破微分方程式；再用普通塑性力学方法求解在岩石中各点的主应力 σ1和 σ2的作用方向，如图4-32 所示。该应力分布状态与图4-30 的应力分布状态极为相似。不同之点是爆轰气体压力所引起的主应力 σ1常为压缩应力，而主应力 σ2并不常为拉伸应力，随距离最小抵抗线超过某一极限距离以后，主应力 σ2变为压缩应力。根据图4-32 中所示的主应力作用方向，可以推断在爆轰气体静压的作用下岩体中产生破坏的裂隙方向。

图4-32　主应力 σ1和 σ2的作用方向