爆炸应力波在岩体中的传播规律探究

冲击波在岩体内传播时，它的强度随传播距离的增加而减小。波的性质和形状也产生相应的变化。根据波的性质、形状和作用性质的不同，可将冲击波的传播过程分为3 个作用区，如图4-21 所示。在离爆源约3～7 倍药包半径的近距离内，冲击波的强度极大，波峰压力一般都大大超过岩石的动抗压强度，故使岩石产生塑性变形或粉碎，因而消耗了大部分的能量，冲击波的参数也发生急剧的衰减。这个距离的范围叫作冲击波作用区。冲击波通过该区以后，由于能量大量消耗，冲击波衰减成不具陡峻波峰的应力波，波阵面上的状态参数变化得比较平缓，波速接近或等于岩石中的声速，岩石的状态变化所需时间大大小于恢复到静止状态所需时间。由于应力波的作用，岩石处于非弹性状态，在岩石中产生变形，可导致岩石的破坏或残余变形。该区称为应力波作用区或压缩应力波作用区。其范围可为120～150 倍药包半径的距离。应力波传过该区后，波的强度进一步衰减，变为弹性波或地震波，波的传播速度等于岩石中的声速，它的作用只能引起岩石质点做弹性振动，而不能使岩石产生破坏，岩石质点离开静止状态的时间等于它恢复到静止状态的时间。故此区称为弹性振动区[13]。

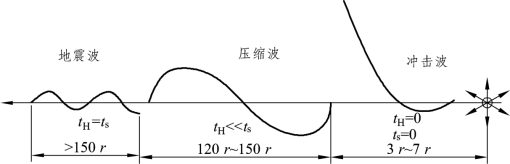
图4-21　爆炸应力波及其作用范围

r—药包半径；tH—介质状态变化时间；tS—介质状态恢复到静止状态时间

1. 爆炸应力波的传播

随着传播距离的增加，爆炸冲击波衰减为爆炸应力波，在研究爆炸应力波传播过程时，必须研究应力波传播时所引起的应力以及应力波本身的传播速度和应力波传播过程中所引起的质点振动速度，这两种速度在数量上存在着一定的关系。

弹性介质中的应力波传播速度取决于介质密度、弹性模量等。在无限介质的三维传播情况下，其纵波和横波的传播速度为：

式中 E—— 介质的弹性模具（kPa）；

ρ —— 介质的泊松比；

G—— 介质的剪切模量（kPa）。

岩石中的应力波速度除与岩石密度、弹性模量有关外，尚与岩石结构、构造特性有关。工程上一般通过实测得出岩石的纵波和横波传播速度。

（1）岩体内动应力与波阻抗和质点速度间的关系。

式中 σ —— 纵波作用产生的正应力；

τ —— 横波作用产生的剪应力；

其他符号意义与前同。

（2）声波在岩体内传播受地质构造控制。

当声波经过层面时，由于介质特性发生变化，将产生透射与反射。一部分能量由于透射而穿过层面继续向前传播，另一部分能量反射回来。若地震波垂直入射到结构面时，入射应力、反射应力和透射应力有如下关系：

(www.xing528.com)

式中 cp1ρ1， cp2ρ2—— 入射侧岩层、透射侧岩层的波阻抗；

i、r、t—— 入射、反射和透射；

σt、 σi、 σr—— 声波在层面产生的透射、入射和反射应力；质点的震动强度也相应地受到岩层的影响；

式中 vt、 vi、 vr—— 振动波经过层面时的透射波、入射波和反射波的质点振动速度。

2. 爆炸应力波在岩体中传播过程的应力、应变衰减规律

（1）应力峰值的衰减。径向应力峰值与传播距离的关系可表示为：

式中 α —— 应力衰减指数。

应力衰减指数与岩石泊松比v 间的经验关系式为：

上式中的“+”号对应于冲击波作用区，“-”号对应于压缩波作用区。

在冲击波作用范围内，岩石的性态类似于流体，这时可取v≈0.5，因此α ≈3 。在压缩波作用区内，按式（4-100）算出的α 值不超过2，但裂隙性岩石的α 值可大于2。故式（4-100）只适用于完整性较好的岩石。

（2）切向应力：岩石在径向应力的rσ 的作用下受到压缩，由于周围岩体的侧限作用，将由此而衍生出切向拉应力σθ 。切向应力峰值（绝对值）可通过径向压应力峰值来表示：

式中的系数rb 与岩石泊松比和爆炸应力波传播距离有关。在爆源附近的rb 值较大（ br≈1）。随着离爆源距离的增大，rb 值迅速减小，并趋于只依赖于泊松比的固定值：

（3）集中药包爆炸时岩石中的径向应变：集中药包在岩体内爆炸时，离药包中心某一距离的近处至远离药包中心相当范围内，岩石中任一点的径向压缩应变最大值（ εrmax）可按下式计算：