爆轰波能量方程与爆炸反应热量QV的关系

因为爆轰波是一种强冲击波，所以爆轰波参数关系式的建立方法与前述冲击波基本相同，不同的是在爆轰波能量方程中增加一项炸药反应放出的热量QV。如图4-10 所示，在稳定爆轰条件下，反应区推进速度（即爆轰波速度）DH与压缩区推进速度（即冲击波速度）D1相等。故在推导关系式时不必考虑反应区，仅比较原始炸药状态和反应区终了状态（即C-J 面）即可。

图4-10　爆轰波参数图（下标“0”表示炸药参数，“H”表示C-J 面上的参数）

由质量守恒关系得：

由动量守恒关系得：

式中 ρ0—— 初始炸药密度；

ρH—— 反应区物质密度；

D —— 爆速；

DH—— 爆炸生成气体气流速度；

pH—— C-J 面上压力，即爆轰压力；

p0—— 初始压力。

由能量守恒关系得：

式中 EH、E0—— 炸药爆轰时和爆轰前的能量；

V0—— 炸药初始质量体积；

VH—— 爆轰波阵面上爆炸气体的质量体积。

考虑到爆轰波反应中要放出热量，故有：

(www.xing528.com)

式中 Q —— 爆热。

式（4-44）是用压力、比容表示的爆轰波能量方程。假定爆轰产物状态变化符合理想气体状态方程，则

又根据理论计算和实验证明，在稳定爆轰时存在下列关系式

式中 cH—— 爆轰产物中的声速。

公式（4-50）叫作爆轰波雨果尼奥（Hugoniot）方程。在图4-11 中的p-V 曲线H1叫作爆轰波雨果尼奥曲线。曲线H2则为冲击波雨果尼奥曲线。在曲线H2上，相对应的各点存在着各种强度的冲击波；然而在曲线H1上，并不是所有的点都与爆轰过程相对应。试验结果表明，在稳定爆轰时存在着如下的关系[11]（详见下一页三）：

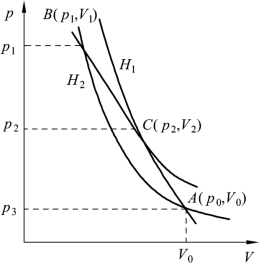
图4-11　爆轰波雨果尼奥曲线

根据上述的爆轰波5 个关系式，并假定K 为常数， p0≪ p2，而忽略，又因D1=DH，可设D1=DH=D，可解出爆轰波主要参数的计算公式如下：

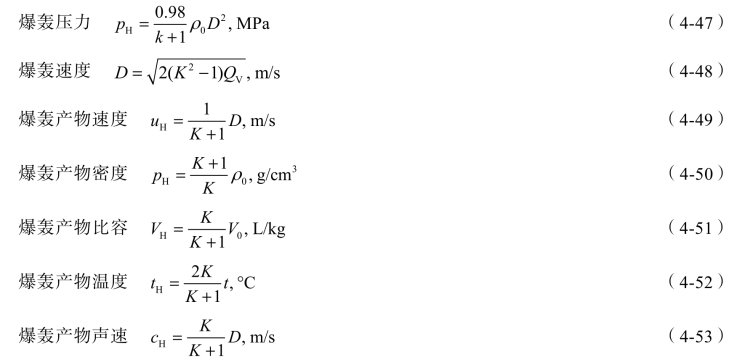
以上式中：t —— 温度，°C。

对于一般工业炸药，近似计算时，可取绝热指数K=3。

上述公式计算的爆轰参数是把爆轰气体当作理想气体，并假定炸药在定容绝热下爆炸，与实际情况有差异，但可满足工业炸药爆破有关计算的需要。

爆速值D 可以通过高速摄影或电测法准确测定，所以常以爆速来计算爆轰波的其他参数。

式中 D —— 爆速；

cH—— C-J 面处爆轰气体产物的声速；

UH—— C-J 面处气体产物质点速度。

由柴普曼和柔格得出的这个公式（4-54）就叫作C-J 方程或C-J 条件。由于C-J 面处满足C-J 条件，爆轰波后面的稀疏波就不能传入爆轰波反应区中。因此，反应区所释放出的能量就不发生损失，而全部用来支持爆轰波的定常传播。