ADRC-PI控制器参数优化

由于这个控制系统中存在两个控制器：自抗扰控制器和PI控制器，因此对其进行的参数整定工作需要分两步进行：首先需要整定内回路的PI控制器，然后整定外回路的自抗扰控制器。

在整定控制器之前，首先需要确定对象的传递函数。本节选择75t/h的国产循环流化床锅炉作为对象，此系统中，主蒸汽温度、减温喷水量及给水流量之间具有强烈的扰动。而且对象模型随着锅炉负荷的变化而发生变化。

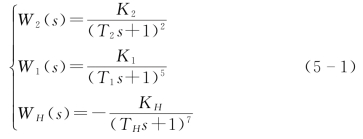
随着负荷由25%变化为100%，各项参数发生如下变化K2=2～1，T2=50～35s；K1=0.8～0.5，T1=100～80s；KH=0.3～0.2，TH=180～150s。

下面选择100%负荷模型为控制对象进行分析。

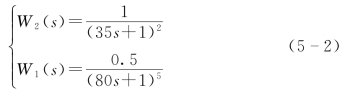
1.安排过渡过程

根据系统的特性，将过渡过程时间选为T0=800s。

2.整定副回路PI控制器

PI控制器的结构为

选用非线性最小二乘法进行整定，得整定结果为Kp=11.9425，Ki=0.1724。

将内回路和W1（s）看作自抗扰控制器的广义对象，并对其进行拟合。拟合后的传递函数为

拟合后的曲线与拟合前的比较如图5-9所示。(www.xing528.com)

3.整定扩张状态观测器

通过时滞环节和惯性环节的特点可知，内回路广义对象可转换为

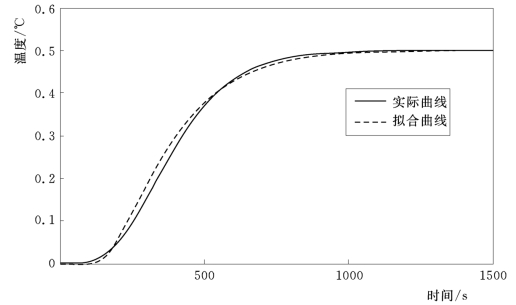
图5-9　内回路拟合曲线效果图

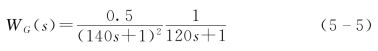
系统的离散化空间状态方程为

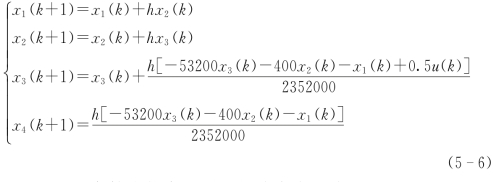
因此，整定扩张状态观测器的阶次为四阶。

将子群设为pop=20，遗传代数设为gen=50，初始子群在[0，100]之间随机产生。最终的优化所得参数为

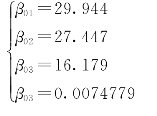
4.整定非线性反馈

依照Levenberg-Marquard 算法整定，取初值为 [1，0，0]，经30步运算，最终优化所得参数为

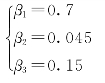
控制系统最终控制效果如图5-9所示。