控制系统数值仿真优化方法

要验证控制系统的控制性能，首选需要整定好控制系统的参数，之后通过引入扰动量和改变工况模型的方法来验证控制系统的抗干扰能力和鲁棒性能。自抗扰控制器的整定根据第三章所提供的自整定算法进行。

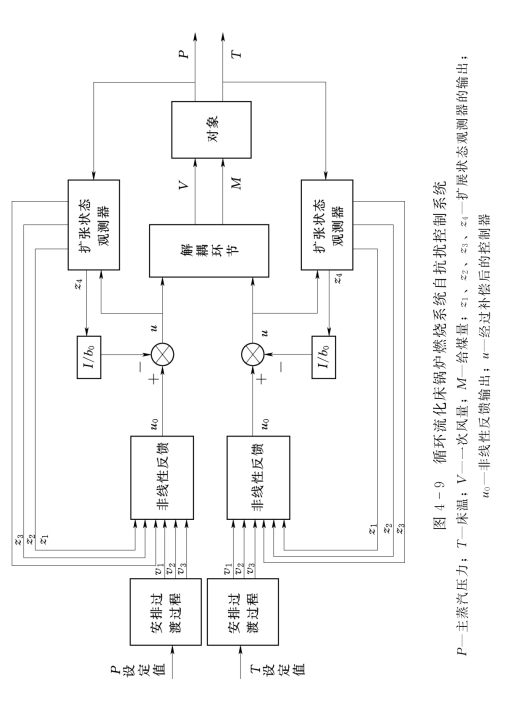
1.主蒸汽压力控制回路的参数整定

此控制回路中，控制对象模型为三阶对象，即

因此需要设计四阶扩张状态观测器和三阶非线性反馈。

对ESO 有

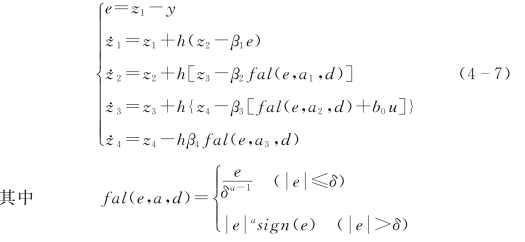
对NLF，有

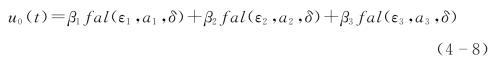
（1）主蒸汽压力控制回路扩张状态观测器 （ESO）参数整定。对象模型的离散化状态空间方程为

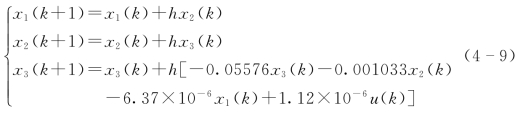
设pop=20，gen=50，初始值取值范围为 [0，100]，h=0.01，δ=0.1，u（k）为阶跃输入。经过NSGA-Ⅱ算法优化，通过择优算法进行择优，确定扩张状态观测器的参数为β01=23.048，β02=37.271，β03=43.145，β04=3.243。

（2）主蒸汽压力控制回路非线性反馈参数整定。根据上步所得扩张状态观测器参数，利用非线性最小二乘法整定非线性反馈参数，初始值设为{1，0，0}，经过40步运算，得整定参数为β1=35，β2=25.1，β3=30.3。

2.床温控制回路控制回路的参数整定

此控制回路中，控制对象模型为三阶函数，即

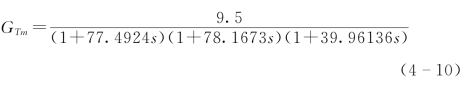
因此，需要构建四阶扩张状态观测器和三阶非线性反馈。

（1）床温控制回路扩张状态观测器参数整定。对象模型的离散化状态空间方程为

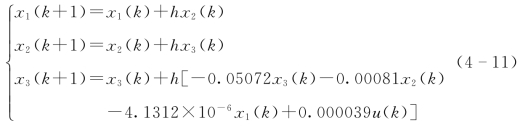
设pop=20，gen=50，初始值取值范围为 [0，100]，h=0.01，δ=0.1，u（k）为阶跃输入。经过NSGA-Ⅱ算法优化，通过择优算法进行择优，确定扩张状态观测器的参数为β01=30.729，β02=23.055，β03=1.145，β04=19.213。(www.xing528.com)

（2）床温控制回路非线性反馈参数整定。根据上步所得扩张状态观测器参数，利用非线性最小二乘法整定非线性反馈参数，初始值设为{1，0，0}，经过45步运算，得整定参数为β1=21，β2=12.2，β3=20.5。

3.循环流化床锅炉燃烧系统自抗扰控制器仿真效果

（1）解耦性能。分别给主蒸汽压力和床温设定值一个阶跃信号，控制系统的响应曲线如图4-10～图4-13所示。其中主蒸汽压力设定值阶跃变化时，主蒸汽压力和床温响应如图4-10和图4-11所示。床温设定值阶跃变化时响应曲线如图4-12和图4-13所示。图中还给出了采用PI控制器时的阶跃响应信号。由曲线的比较可知，自抗扰控制器 （ADRC）在解耦性能、快速性能及稳定性上，要明显优于PI控制器。

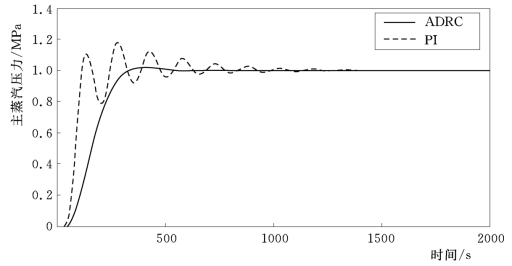
图4-10　主蒸汽压力设定值阶跃时主蒸汽压力响应曲线

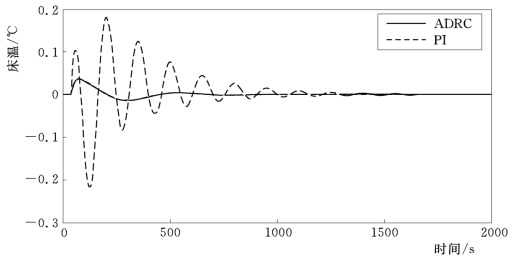
图4-11　主蒸汽压力设定值阶跃时床温响应曲线

（2）模型适应性。使用100%负荷下整定的参数，将对象模型转换为75%负荷模型，自抗扰控制器的响应曲线如图4-14和图4-15所示。比较两种负荷时的响应曲线可知，自抗扰控制器的模型适应性很好。

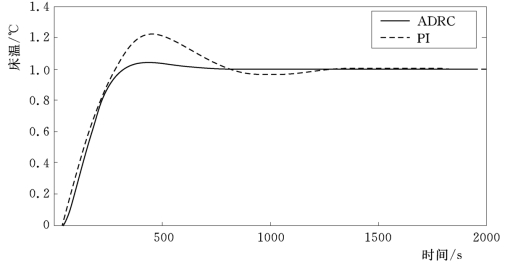
图4-12　床温设定值阶跃时床温响应曲线

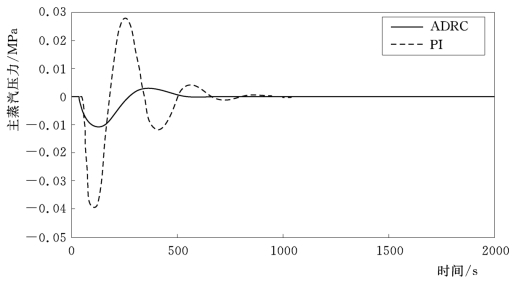
图4-13　床温设定值阶跃时主蒸汽压力响应曲线

（3）抗干扰性能。对于100%负荷模型，在1000s时，分别给对象加入一个幅值为0.2的扰动信号（在输出位置加入，代表外部扰动，如二次风引起的突变等）。此时主蒸汽压力设定值阶跃时，主蒸汽压力的响应曲线如图4-16所示，床温设定值阶跃时，床温的响应曲线如图4-17所示。仿真结果证明自抗扰控制器具有很好的抗干扰性能，能够很快地返回稳定状态。

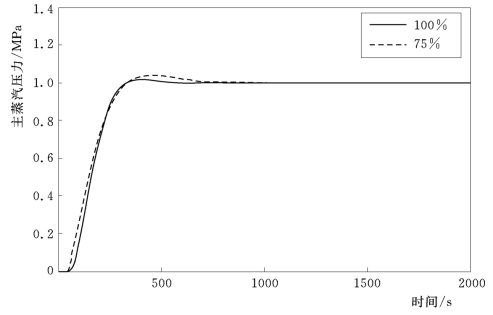
图4-14　75%负荷主蒸汽压力设定值阶跃时主蒸汽压力响应曲线

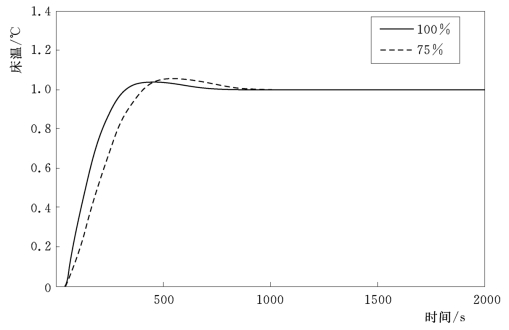
图4-15　75%负荷床温设定值阶跃时床温响应曲线

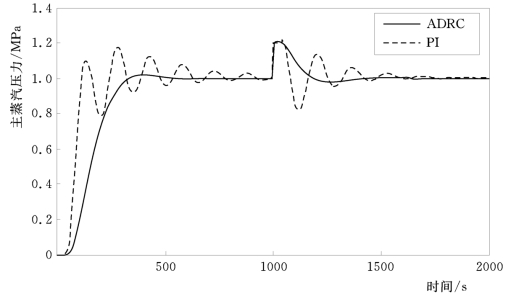
图4-16　增加阶跃扰动时主蒸汽压力设定值阶跃下主蒸汽压力响应曲线

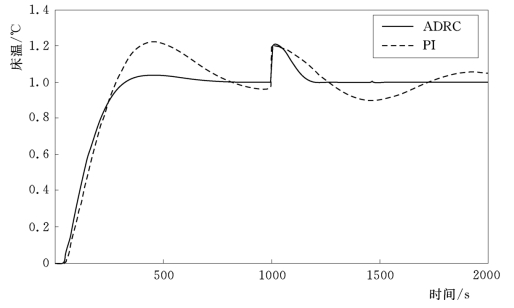
图4-17　增加阶跃扰动时床温设定值阶跃下床温响应曲线