选择控制对象为

式中 x1、x2——系统的空间状态变量;
u——输入;
y——输出;
Asign(sin(ωt))——系统中的不确定部分和扰动。
现在定义x3=Asign(sin(ωt)),取1≤A≤10,0≤ω≤0.5。
1.跟踪微分器的整定
取输入为阶跃输入,将过渡时间设为1.4s,则根据跟踪微分器的整定原则,整定对应参数为r=2,h=0.01。此时跟踪微分器的输出曲线如图3-4所示。

图3-4 跟踪微分器曲线
2.扩张状态观测器的整定
由于控制对象为二阶控制对象,因此扩张状态观测器为三阶。在扩张状态观测器的优化算法中,选择优化目标函数组
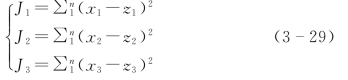
现设定h=0.01,遗传代数gen=20,群体大小pop=20,仿真时间t=20s。优化所得的pareto解见表3-1。
表3-1中前三列为优化的参数,之后三列为优化目标值,最后一列为非支配序列。由表3-1可见,群中尚未达到全部为非支配集合。
对所得pareto解进行择优,确定整定参数为β1=122.91,β2=180.16,β3=939.12,z1、z2 和z3 和跟踪效果如图3-5~图3-7所示。(https://www.xing528.com)
表3-1 优化结果1 (gen=20)
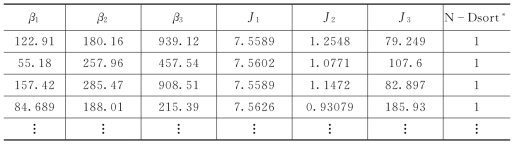
* N-D Sort表示优化结果中的非支配序列。

图3-5 x1-z1 的观测图

图3-6 x2-z2 的观测图
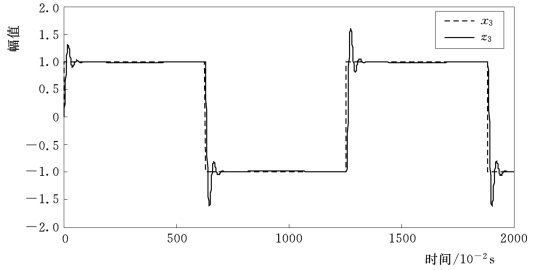
图3-7 x3-z3 的观测图
之后,保持种群大小不变,将迭代次数扩大到100,重新进行优化,择优所得参数为β1 =108.4,β2 =302.01,β3 =996.321,z3 的跟踪效果如图3-8所示。

图3-8 增加迭代次数后x3-z3 的观测图
3.非线性反馈的整定
按照前面所整定的跟踪微分器和扩张状态观测器的参数,选取Levenberg-Marquard算法的初始值β1=1,β2=0。按整定流程优化,15步以后得到优化结果β1=1050,β2=39。此时系统闭环响应曲线如图3-9所示。

图3-9 整定输出与设定值曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




