NSGA-Ⅱ算法在扩张状态观测器整定中的注意事项

在应用NSGA-Ⅱ算法对ESO 参数进行整定的时候需要对NSGA-Ⅱ算法进行一些改进，整定算法实现步骤如下：

（1）把对象传递函数转化为离散的状态空间形式，编程计算对象的状态空间变量以及系统不确定部分，作为扩张状态观测器观测的依据以及优化目标的计算基础。

（2）在一定范围之内产生pop （子群大小）组随机参数，利用随机参数和对象的输出编程实现扩张状态观测器计算，产生对应的状态空间变量观测值和扩张状态的观测值；利用实际变量和观测值计算所对应的优化目标值。

（3）进入NSGA-Ⅱ主计算流程，直至达到设定的gen （遗传代数）。

1.pareto解择优问题的解决

由于多目标优化算法产生的pareto解是包含pop 优化解的解集，为了确定扩张状态观测器的整定参数，需要从其中选择出一个更合适的解。人工选择方法可选以下两种之一：第一种是采用排序（基于非支配排序与拥挤度排序）第一的解；第二种是先选择出第一个优化目标值最优的解集，然后由其中再选择出最后一个优化目标值最优的一个解，即将扩张状态的观测情况视为最坏，作为评价标准。

人工选择方法尽管能够满足大多数低阶整定问题的需求，对于一些复杂的情况也难尽人意。因此本书采用基于模糊理论的pareto寻优方法。

定义函数μi 表示pareto 解中第i 个体的目标值所占权重，则

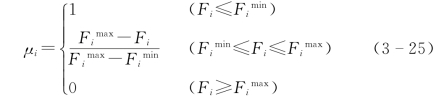
式中　——第i个目标值的最大值和最小值。

对pareto解中每个非支配解定义等级函数值μk，则

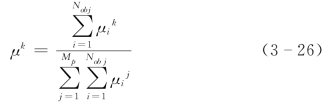
式中　Nobj——目标函数的个数；

　　　Mp——pareto解中非支配解个数。(www.xing528.com)

对于每个非支配解来说，式 （3-26）函数值越大，说明该解综合性能越好。因此，选择该函数值最大的非支配解为扩张状态观测器的最终整定参数。

2.交叉算子

NSGA-Ⅱ提供了两种参数编码方法：二进制编码和实型编码。本书增加遗传算法的全局搜索范围，采用算术交叉算子，即

式中　a、b——[-0.5，1.5]之间的随机数，并且a+b=1。

3.增加约束条件

由于增大了搜索范围，因此，在进行遗传运算时，会出现一些不可用量。此时，表现为优化目标值超出许可范围，比如Ji为正无穷。为了提高算法整体的效率，需要增加约束调节，对产生的优化解进行取舍。

具体做法为增加优化目标值的取值范围Xi，i=1，…，Nobj（Nobj为目标函数数目）。

（1）若Ji≤Xi，所得解保留，可进入下一步迭代。

（2）若Ji＞Xi，则放弃此解重新进行遗传或变异。若发生在第一代，则在初始范围内随机产生。

考虑到需要约束第一代，约束范围不宜过小，一般而言±100即能满足要求。

4.对于复杂对象的整定

若需整定对象过于复杂，可利用经验缩小初始化范围，缩短运算流程。对于没有经验的设计人员而言，可以采用多次优化的方法来进行，即每次的优化范围根据上次优化的结果来缩小，或者可以增加迭代次数来进行，但是这样会增加优化算法的计算量。

基于NSGA-Ⅱ整定扩张状态观测器流程如图3-2所示。