自抗扰控制器的原理解析

自抗扰控制器是基于跟踪微分器安排过渡过程，利用扩张状态观测器估计系统状态及外扰的一种非线性控制器。在这个控制器中，利用扩张状态观测器提取为实现状态反馈及外扰补偿所需的信息。系统的外扰可用扩张状态观测器估计出实时作用量而给以补偿。扩张状态观测器是把有未知外扰的非线性不确定对象用非线性状态反馈化为积分器串联型对象，是一种对非线性不确定对象实现反馈线性化的结构。把系统化为积分器串联型以后，就能对其用状态误差反馈来设计出理想的控制器。

自抗扰控制器主要由四部分组成，即安排过渡过程或跟踪微分器（TD）、ESO、非线性状态误差反馈控制律（NLF）和扰动估计补偿部分。其中TD 的作用是根据设定值的大小安排过渡过程，并提取出其微分信号；ESO 用于根据被控对象输入、输出估计出系统的状态和扰动总和；NLSEF 根据系统误差计算出控制量，扰动估计补偿是将ESO 估计出的总扰动补偿到NLSEF计算出的控制量上，得到被控对象的实际控制量。图3-1给出了二阶自抗扰控制器的结构图。

图3-1　二阶自抗扰控制器结构图

1.安排过渡过程

在工业现场的过程控制中，有很大一部分是对被调量的设定值控制，当设定值发生改变时，工业过程从一个平衡点过渡到另一个平衡点。在这个过程中，系统有时会产生剧烈的变化，这通常会造成控制系统的快速性和超调量之间的矛盾。现场为了避免这一点，有时候会对设定值的变化率进行限制。这就是安排过渡过程的一种最简单的形式。

安排过渡过程是自抗扰控制器的一个重要内容。通过合理地安排过渡过程，减小对系统的冲击，能够有效地实现系统的“无超调，快速跟踪控制目标”，并且使得误差反馈和误差微分反馈增益的选取范围大为扩大，增加系统的鲁棒性。

下面给出二阶对象和三阶对象的一种过渡过程设计形式。

（1）二阶对象。选取过渡过程的加速度函数为

式中　v0——设定值；

　　　T0——设定的过渡时间，过渡时间根据对象的不同而不同。

则过渡过程为加速度的二次积分。

（2）三阶对象。选取过渡过程的加速度函数为

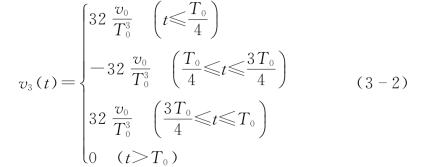
则过渡过程为加速度的三次积分。

2.跟踪微分器（TD）

在传统的PID 控制器中通常使用微分器处理微分调节作用。理想的微分器其时域函数和传递函数的形式为

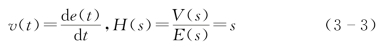
但是在实际应用过程中，理论微分通常难以实现，因此实际应用过程中，理论微分器被改变为实际微分器，其传递函数的形式为

当时间常数Td≪1时，这个实际微分器可替代为理想微分器，且其输出信号随着时间常数的缩小，越来越逼近于实际的速度信号。但是随着时间常数的缩小，往往也会带来一些高频扰动信号。

针对传统微分器的研究，韩京清先生提出了针对如下系统的一种离散最速控制综合函数fhan，这个函数称为跟踪微分器作用。

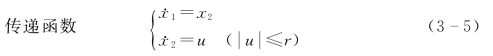
最速控制综合函数

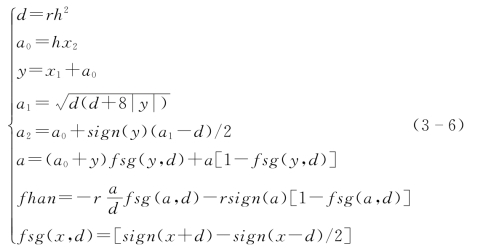
由此可见，所谓跟踪微分器是这样的机构：对它输入信号v（t），它将输出两个信号z1 和z2，其中z1 跟踪v（t），而z2=，从而把z2 作为v（t）的“近似微分”。常用两种跟踪微分器的形式如下：

（1）第一种形式为

式中　v——输入信号；

　　　r——跟踪微分器的快慢因子，r 越大，z1 越接近v，z2越接近v 的导数或广义导数，跟踪效果越好；r 越小跟踪效果越差；

　　　β1、β2——跟踪快慢的微调因子，同时也表示跟踪信号z1 和z2有无超调和超调大小的因子。

函数fal（z，α，δ）则为

（2）第二种形式为(www.xing528.com)

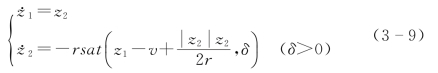
式中　r——跟踪微分器的快慢因子；

　　　δ——线性区间的大小。

函数sat（z，δ）为

由上面的跟踪微分器的结构可知，跟踪微分器可通过改变参数实现安排过渡过程。此外，它还有着相当广泛的用途，扩张状态观测器就是基于跟踪微分器研究得到的。

3.扩张状态观测器（ESO）

控制系统中扰动影响系统的控制性能，甚至导致系统不稳定。闭环控制中的负反馈虽然能够抑制住一定的系统干扰，但是能力却是非常有限的。从控制系统设计的角度来看，主要关心影响系统输出的干扰，因此估计和抑制具有影响系统输出的扰动是状态观测器的关键。基于这个目的，借用状态观测器的思想，将系统的输出中的干扰项作为扩张状态加入到状态观测器中，作为状态观测器一个新的状态，从而得到一个新的状态观测器被称为扩张状态观测器（ESO）。这个扩张观测器不需要知道系统扰动本身的任何先验知识，也不需要直接测量系统干扰，只需要测得被控对象的输入和输出信息，就可以实时跟踪估计出系统状态和系统总扰动。

对于外扰未知的非线性不确定对象

式中　f（x，x（1），x（2），…，x（n-1），t）——未知函数；

　　　w（t）——未知外扰。

若以x （t）为测量值，由于扩张状态变量x （t）、 （t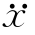）、 （t）、…、x（n-1） （t）、x（n） （t）是测量值x（t）的各阶导数，因此观测器型的跟踪微分器[97]能够解决上述问题。

构造如下形式的非线性系统

式中，gi（t），i=1，…，n为非线性函数。

使以测量值x（t）为输入的系统各状态分别跟踪原状态变量，即有

适当选取gi（t），上述目的是可以实现的。大量的数值仿真表明了这种观测器设计的合理性和有效性[101-104]。二阶扩张状态观测器已经进行了稳定性证明和误差分析[105]。

扩张状态观测器中特别有意义情况是，当记a（t）=f（x，x（1），x（2），…x（n-1），t）+w（t）时，则有zn+1（t）→x（n）（t）=a（t），即尽管函数f（x，x（1），x（2），…x（n-1），t）和外扰w（t）未知，但系统运行过程中的实时值a（t）仍能估计出来。这在不确定受控对象的控制器设计中，实现“模型和未知外扰补偿”是非常重要的。

目前常用的扩张状态观测器形式如下：

式中　e——输出与输出观测之间的偏差；

　　　h——采样周期；

　　　β0i——观测器参数，i=1，…，n+1。

4.非线性反馈（NLF）

经典PID 是将系统误差的过去、现在和变化趋势简单地进行线性加权组合来得到系统的控制量。这种方式虽然简单，但是无法解决快速性和超调之间的矛盾。而其他许多非线性组合方式可能具有很好的控制性能。扩张状态观测器观测出系统的状态变量和扩展状态变量，将这些状态变量与TD 规划出的系统输出量相减形成系统的误差量，即

通过对这些误差信号的非线性组合，就可以构成一种性能良好的非线性反馈控制，常见的非线性组合如下：

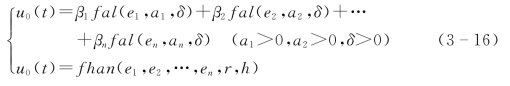
式中　β1、β2——可调的反馈系数；

　　　a1、a2——适当的正数；

　　　δ——线性区间的大小。