实现比例因子自调整的模糊控制算法

为进一步改善系统的动态性能，采用5.4节设计的比例因子自调整二维模糊控制器取替图8-2所示的以8098单片机为核心运行在电压PWM方式下的0.75kW SR电动机DDC系统中PI调节器。

将5.4.1节设计的模糊控制决策表（见表5-3）存放在EPROM内。速度环程序中，将实测的速度偏差e（给定速度-实际转速）、偏差变化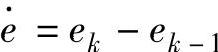分别乘上量化因子α_E、α_EC转换成模糊论域中的元素，然后查表5-3得对应的控制输出U，再据式（5-76）得控制占空比的参数HTIME（kT）。

查表5-3的方法较简单，将偏差变化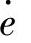模糊量转换成表格的列序号i，偏差e模糊量转换成行号j，则可确定输出控制量在表中的相应位置为：i+15j，再加上表格的首地址，用8098数据传送指令即可实现模糊控制算法，其流程如图8-8所示。

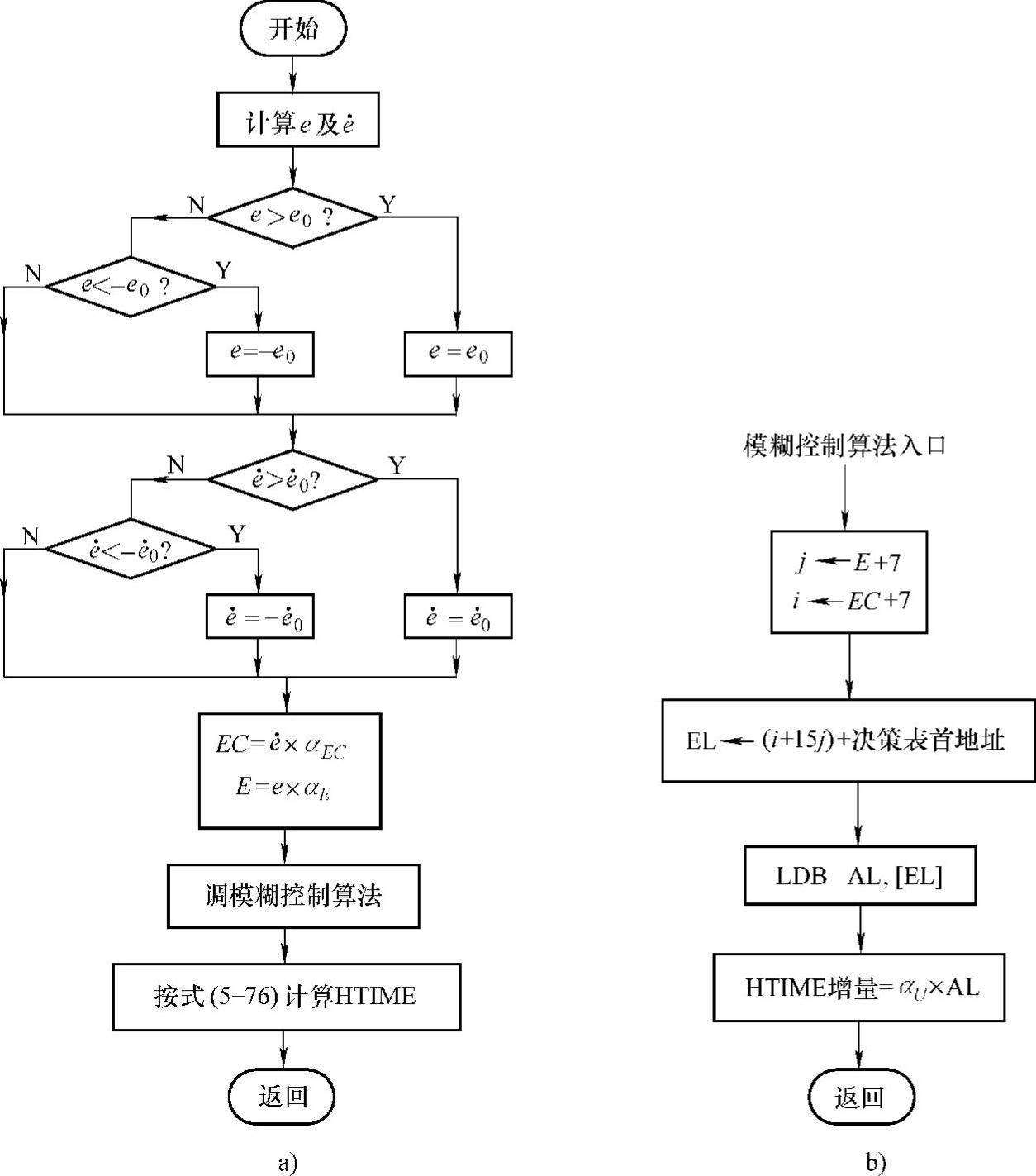
图8-8 基于模糊控制的速度环流程图

a）速度环流程 b）模糊控制算法流程（固定参数）

从图8-8a可以看出，速度环首先计算实际的e及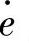，然后判断其是否在约束区间[-e₀，e₀]及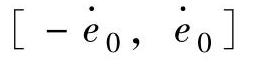内，若越出约束区间，则令其为相应的区间边界值。这是必要的，因为系统运行实验表明，若按实际可能出现的e及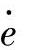最大变化范围[-e₁，e₁]及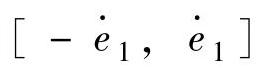确定量化因子[α_E=14/（2e₁），α_EC=14/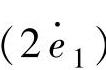]，因量化因子小，在接近暂稳态时，分辨率差，系统性能不佳。因此，在参数固定的模糊控制系统程序设计中，应以一合适的小于实际变化范围的区间[-e₀，e₀]及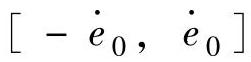来确定量化因子，即α_E=14/（2e₀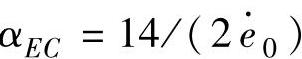），，这样，为了使与实际的e及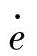对应的模糊量不超出论域的范围，需对实际的e及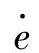用约束条件加以判断、限幅。(www.xing528.com)

从图8-8b所示可见，模糊控制算法是通过查表的方法实现的。

如5.4.2节所述，为了改善模糊控制器的性能且兼顾实时性，将偏差量化因子离线整定为α_E=0.0175，e的约束区间取[-400，+400]；偏差变化量化因子离线整定为α_EC=0.035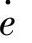，的约束区间取[-200，+200]；在线查询表5-4，获得自调整的比例因子α_U。

比例因子自调整模糊控制算法流程如图8-9所示，图中，字节寄存器AH存放查询到的比例因子α_U，字节寄存器AL存放查询到的控制量。

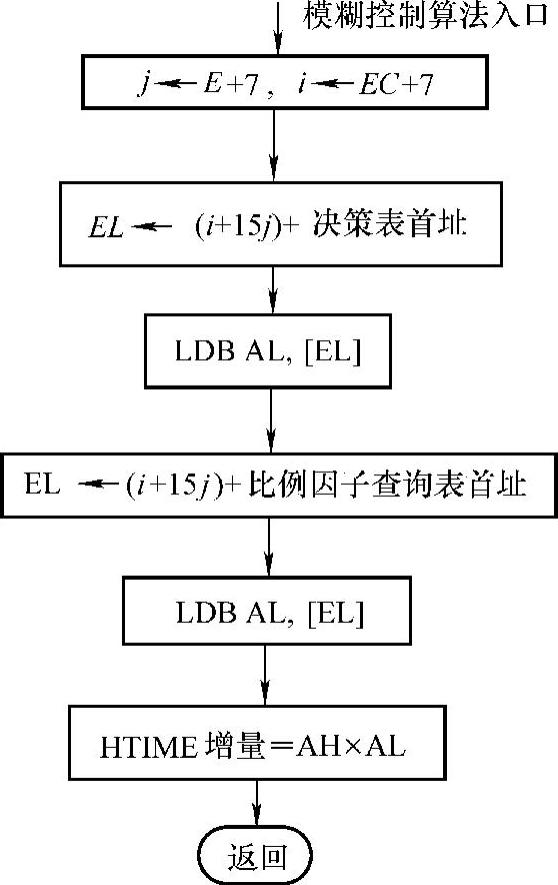
图8-9 比例因子自调整模糊控制算法流程