SR电动机定子振动特性的机电类比分析

7.3.2.1 SR电动机振动响应的解析分析

目前，在工业上通用调速场合应用的SR电动机通常采用与Y系列异步电动机类比的方法设计^[11]，一般选用同功率的异步电机机座，定子铁心与机壳内圆采用过盈配合，无连接筋。设定子铁心磁轭刚度为K₁、质量为m₁、机壳的质量为m₂、刚度为K₂，绕组、磁极的影响通过附加质量归入铁心磁轭，冷却筋、底脚、接线盒的质量归入机壳；并设各部分的粘性阻尼系数分别为r_m1、r_m2，则其物理模型、机械网络、等效电路如图7-14所示。

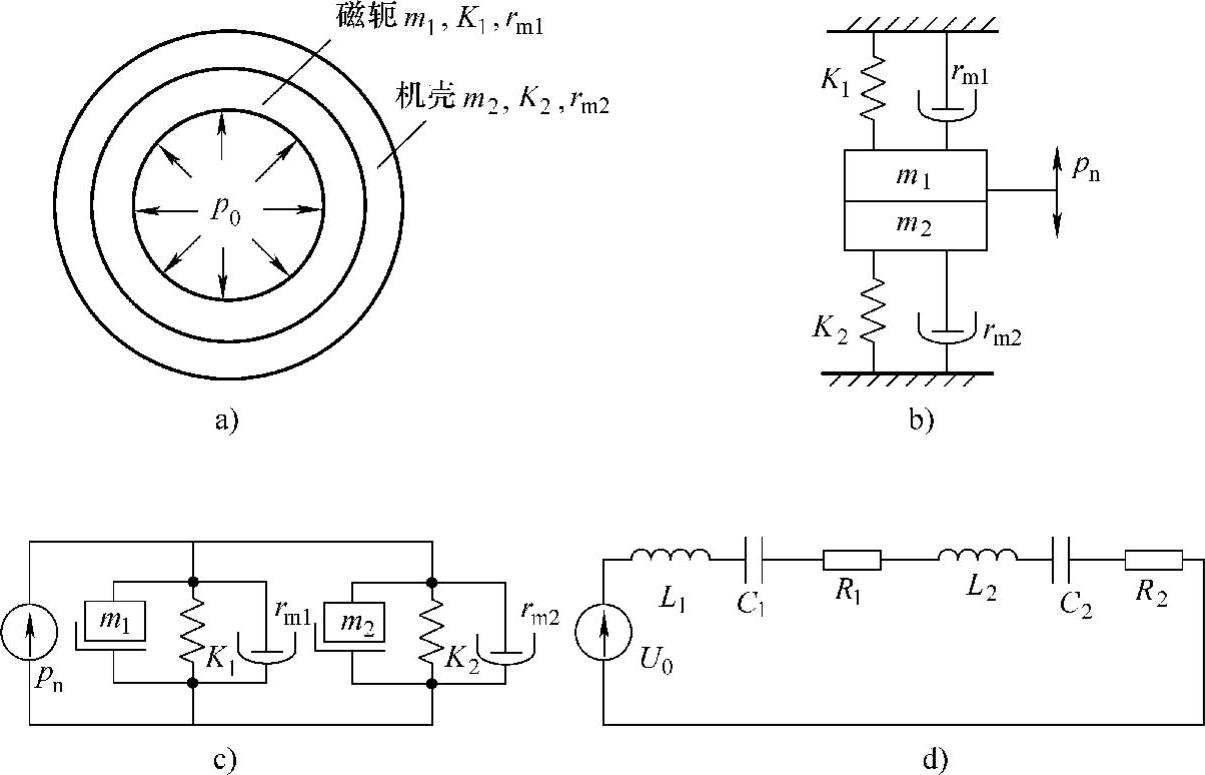
图7-14 SR电动机定子振动特性机电类比分析

a）简化SR电动机定子原型 b）物理模型 c）机械网络 d）对应的等效电路

图7-14中，p₀为作用在定子铁心内表面上单位面积力的幅值，p_n为等效的集中力，即

p_n=2πR_il_ap₀ （7-13）

式中，R_i为定子磁轭的内半径；l_a为定子铁心叠片长度。

SR电动机相绕组中的励磁电流系周期为T的脉动电流，由此脉动电流引起的电磁力不仅有直流分量和基频ω₀（=2π/T）处的分量，亦有ω₀的各次谐波分量，由机电类比可得对应角频率ω的总机械阻抗为

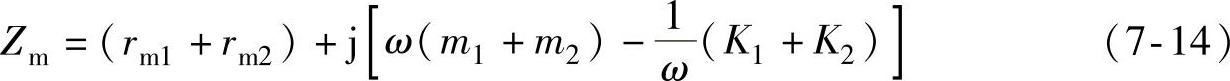
铁心和机壳的振动速度为

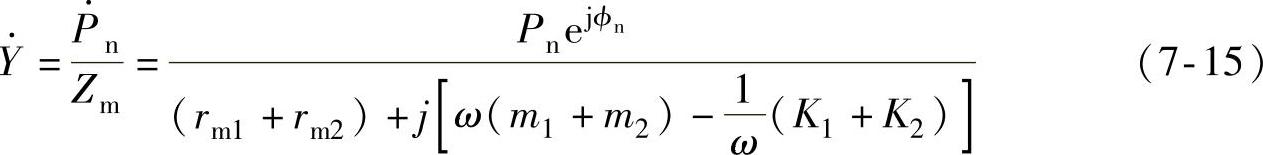
式中，铁心及机壳的刚度和质量分别为[158]

式中，G₁为铁心、绕组的总质量（kg）；G₂为机壳、冷却筋、底座的总质量（kg）；R₁为铁心磁轭的平均半径（m）；R₂为机壳的平均半径（m）；J₁为铁心磁轭轴向截面对其轴向中心线的惯性矩（m⁴），J₁=（h_cs³l_a）/12，其中h_cs为铁心轭厚（m），l_a为铁心叠片长度（m）；J₂为机壳轭部轴向截面对其轴向中心线的惯性矩（m⁴），J₂=（h_fs³l_f）/12，其中h_fs为机壳轭厚（m），l_f为机壳长度（m）；E₁、E₂分别为铁心材料、机壳材料的弹性模量（N/m²）；F_n1、F_n2分别为铁心、机壳的轭厚与平均半径之比的函数^[158]；n为振型阶数。

设铁心、机壳的阻尼比ξ₁、ξ₂为粘性，且分别等于钢、铸铁的阻尼比，则阻尼系数为

由式（7-15），可求得SR电动机定子振动位移的幅值为

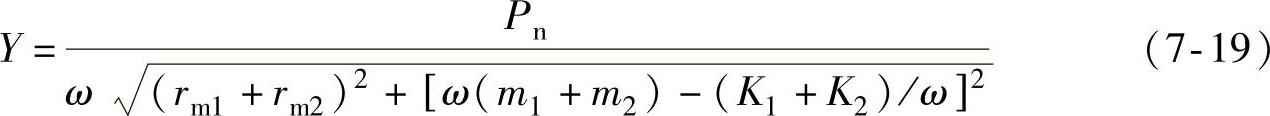
令机械阻抗的虚部为零，可求得定子的固有圆频率为

则自由振动固有频率为

共振时，定子振动位移的振幅为

将式（7-16）、式（7-17）代入式（7-19）、式（7-21），可得SR电动机固有频率和强迫振动幅值为(www.xing528.com)

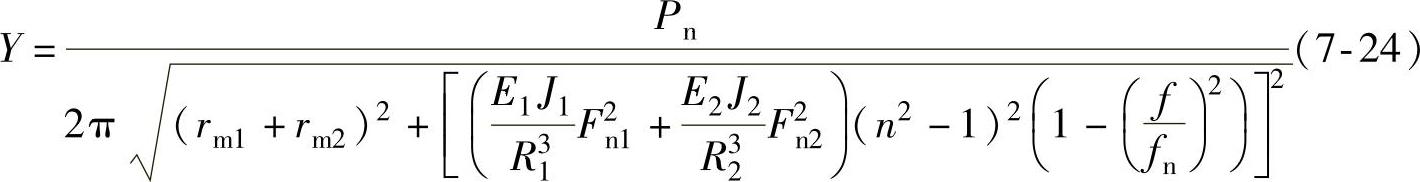
由式（7-23）、式（7-24）可得SR电动机轴向阶数为零的平面振动具有如下特性：

1）随着振型阶数n的增大，对应的固有频率近似以n²的比例增大，而振幅则近似以n⁴的比例减小，因此阶数较低的力波引起的振动，如2阶椭圆形变，应是防范的重点。

2）定子直径越大，固有频率越低，亦即当激励力的振幅、频率均相等时，几何尺寸越大的电动机，振动幅值越大，因而磁噪声级亦越大。

3）振动大小与振动系统的阻抗Z_m关系很大，阻抗表明振动系统接近谐振的程度。谐振时振动甚至在小的激振力时都可能很大。因此，使固有频率避开主要的激振力波频率是减小振动的重要措施之一。

4）振动振幅与径向力波的振幅成正比。因此控制径向力波幅值是控制振动的重要措施之一。

5）共振时激振力波与振动速度同相位，这时振动幅值由阻尼限制。SR电动机定子铁心由叠片组成，并且有绕组，实践证明^[158]：叠片铁心的阻尼比大于钢的阻尼比，绕组的存在又增加了阻尼比，因此SR电动机的共振振幅并非无穷大。但从抑制振动、噪声角度来看，避免共振是很重要的。

7.3.2.2 SR电动机固有频率的解析计算

运用式（7-21）计算固有频率的关键是正确计算铁心及机壳的刚度和质量。如前所述，参考文献[158]在推导固有频率计算式（7-23）的过程中，将电动机定子齿和绕组的影响通过附加质量而归入铁心，冷却筋、底脚等的质量归入机壳，这对于传统交、直流电动机固有频率的计算是有一定精度的，但对于结构有其特殊性的SR电动机并不完全适用。事实上，由于存在定子凸极、相绕组、机壳冷却筋、机壳底脚、接线盒等结构，SR电动机定子质量及刚度在圆周上并非均布，其实际振动特性与均匀对称“圆环”的振动差异较大，若按传统的机电类比分析方法计算，将导致较大的误差。鉴于机壳不对称结构在传统电动机中也存在，定子凸极和定子集中绕组才是SR电动机定子结构的特色。因此，在处理机壳不对称结构时仍沿用传统的方法，即将冷却筋、底脚等的质量归入机壳，忽略其对机壳刚度的影响；而SR电动机相绕组、定子凸极不仅增加了定子铁心的质量，而且增加了其刚度，故不应仅以附加质量归入定子磁轭。有限元分析表明^[165，204]：相绕组对定子铁心固有频率的影响不仅有质量方面的因素，且有刚度方面的因素，总体上，相绕组对定子铁心固有频率的影响较小^[165]，可认为其对定子铁心固有频率的双重影响近似相抵^[204]。有鉴于此，在应用式（7-23）计算固有频率时，可不计定子绕组的影响，对定子凸极则不仅将其质量归算到定子磁轭中，同时将离散分布的定子凸极的质量按质量相等原则等效为均匀分布在圆周上，据此计算等效轭厚h_cs^∗及等效的磁轭平均半径R₁^∗，从而等效计入定子凸极对磁轭刚度的影响。设定子极数为N_s，极宽为b_ps，定子铁心密度为ρ₁，如图7-15所示，即可按式（7-25）～式（7-29）归算定子凸极对磁轭质量和刚度的影响。

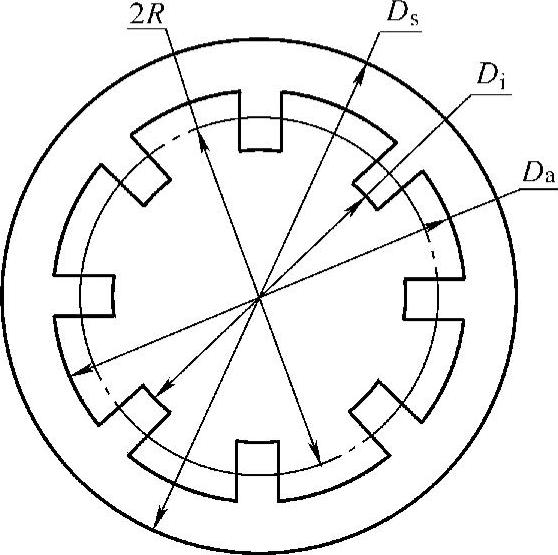
图7-15 四相（8/6）SR电动机定子冲片图

令

解出

则归算定子凸极后，等效的磁轭平均半径R₁^∗及等效的轭厚h_cs^∗分别为

按以上定子凸极归算算法计算了样机1和样机2的固有频率，其材料参数仍按表7-1选取，计算结果见表7-2。表7-2同时给出了采用另外两种解析计算方法的计算结果，其一，不计定子绕组影响，定子凸极仅以附加质量归入磁轭但不计其刚度影响；其二为传统解析计算方法，即定子凸极、绕组均以附加质量（计算绕组质量时，铜导线的密度取8900kg/m³）归入磁轭，但不计其刚度影响。为了检验解析计算的准确度，表7-2亦列入了7.3.1节2D有限元计算的结果。对有限元计算获得的“非标准”模态，若其振型特征与某阶模态较接近，则将其近似归为对应于该阶模态；但若其振型特征不明显，难以近似处理，则舍弃该“非标准”模态。表7-2表明，与2D有限元计算结果比较，基于定子凸极归算算法解析计算低阶固有频率具有良好准确度；而传统解析计算方法计算结果明显偏低，误差较大。样机1和样机2的实验模态分析结果^[163]表明，2D有限元计算2阶固有频率有良好准确度，因此以2D有限元分析结果检验SR电动机轴向阶数为零的低阶固有频率解析计算准确度是合理的。

表7-2 固有频率计算值（分别采用解析计算和2D有限元计算）

应该指出，上述有限元计算和解析计算中，为了简便，铁心的弹性模量及密度均是按实心钢材选取的。但实际铁心由硅钢片叠压而成，从提高计算精度的角度出发，应考虑叠压对弹性模量和密度的影响。参考文献[204]取叠片铁心的材料密度ρ_l为

ρl=KlρFe （7-30）

式中，ρ_Fe=7750kg/m³；K_l=0.95为叠压系数。

已有研究表明，对于轴向阶数m≠0的振动，叠片铁心的刚度显著小于整块铁心^[165]。参考文献[165]针对SR电动机轴向阶数m=0的振动，计算和实验结果表明，叠片铁心的弹性模量与整块铁心相同，但该结论是对应叠片铁心在圆周6个位置处均沿轴向作了焊接且不带机座的情形得出的，而实际SR电动机的定子叠片铁心安装在机座中。因此，在分析、计算SR电动机定子振动模态和固有频率时，如何合理施加定子铁心材料属性，仍需进一步研究。