转矩分配函数法简介

SR电动机转矩脉动主要是因其各相产生电磁转矩的非线性特性及相绕组激励的离散性所致。为了量化SR电动机的转矩脉动，定义转矩脉动率k_T为^[127]

式中，T_max、T_min分别为合成瞬时转矩的最大值、最小值；T_avg为合成转矩的平均值。

SR电动机相绕组换相时，若按常规控制方法开通、关断相电流，会使得开通相形成的转矩增加量不足以抵偿关断相引起的转矩减小量，从而导致合成瞬时转矩明显跌落，因此换相时转矩脉动问题更为突出。有鉴于此，转矩分配函数法以合成瞬时转矩恒定为目标，通过转矩分配函数（TSF）分配各相在不同位置的期望转矩，并通过转矩/磁链/电流滞环控制或转矩/磁链/电流PWM控制使合成瞬时转矩跟踪由位置闭环或速度闭环控制器输出的指令转矩。TSF法不适用于APC单脉冲控制方式。在换相期间，TSF法并非控制相电流的变化率，而是控制转矩的变化率，以实现均衡换相，抑制转矩脉动。定义第j相转矩的分配函数为f_j（θ），则据TSF法的控制目标，有

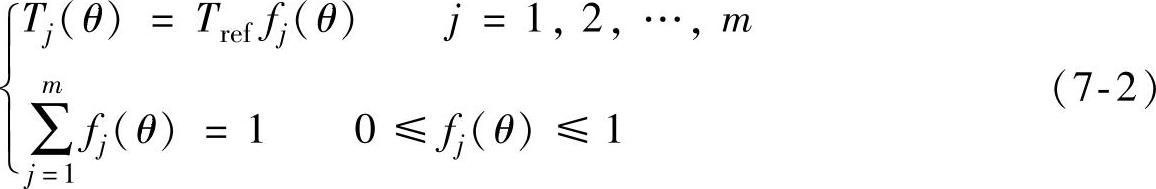
式中，m为SR电动机的相数；T_j为第j相瞬时转矩；T_ref为合成瞬时转矩指令值。

合理设计TSF，对于高性能SR电动机控制非常重要，其一般按如下原则设计^[201]：各相仅产生正的（电动）转矩；任一瞬时，仅有一相绕组或相邻两相绕组通电励磁。典型的TSF有直线型、指数型、正弦型、立方型四种^[183，201]，如图7-1所示。

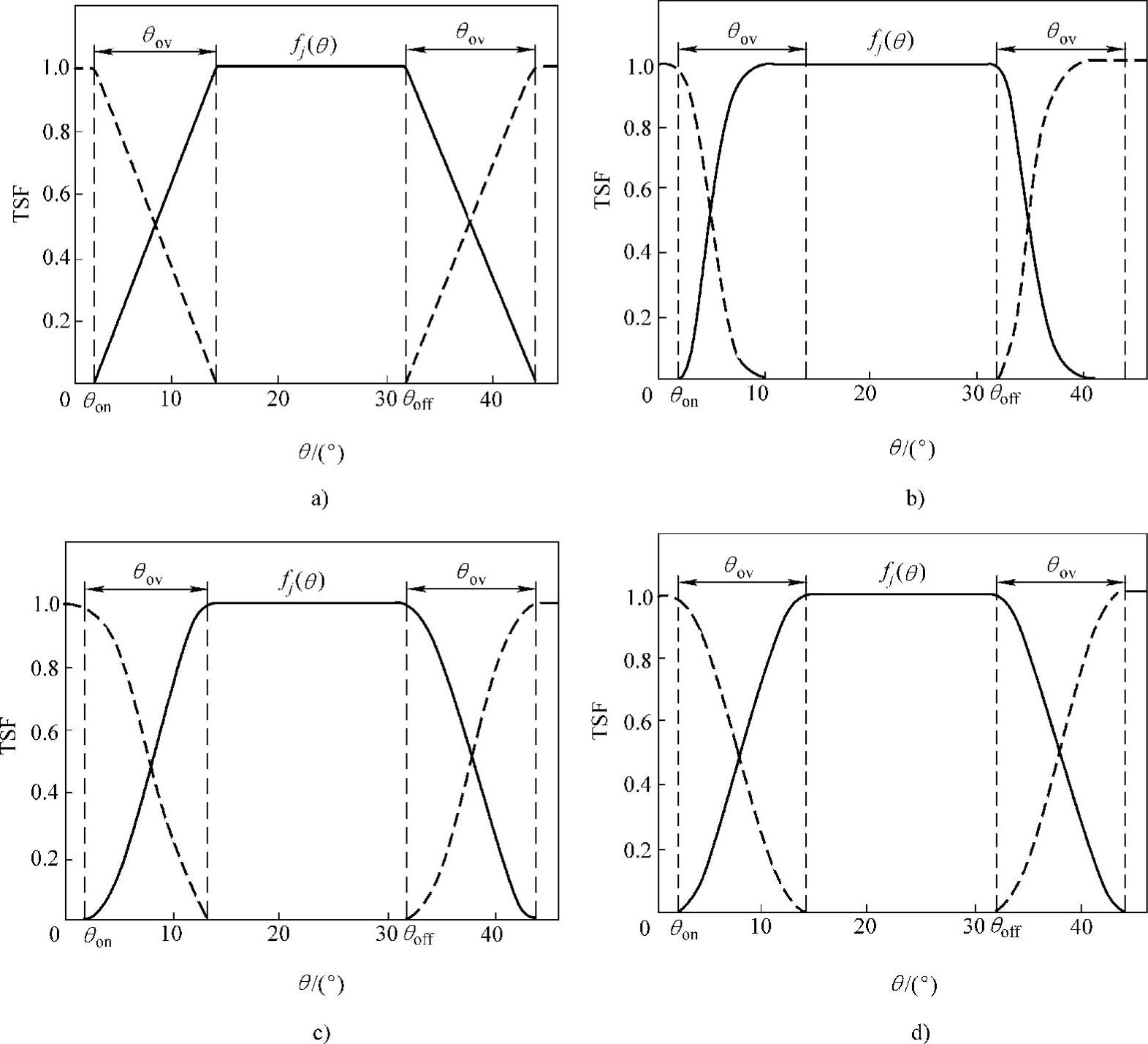
图7-1 典型的TSF波形（以三相（6/4极）SR电动机为例）

a）直线型 b）指数型 c）正弦型 d）立方型

1.直线型TSF

如图7-1a所示，在一个转子角周期τ_r内，第j相转矩的直线型分配函数为

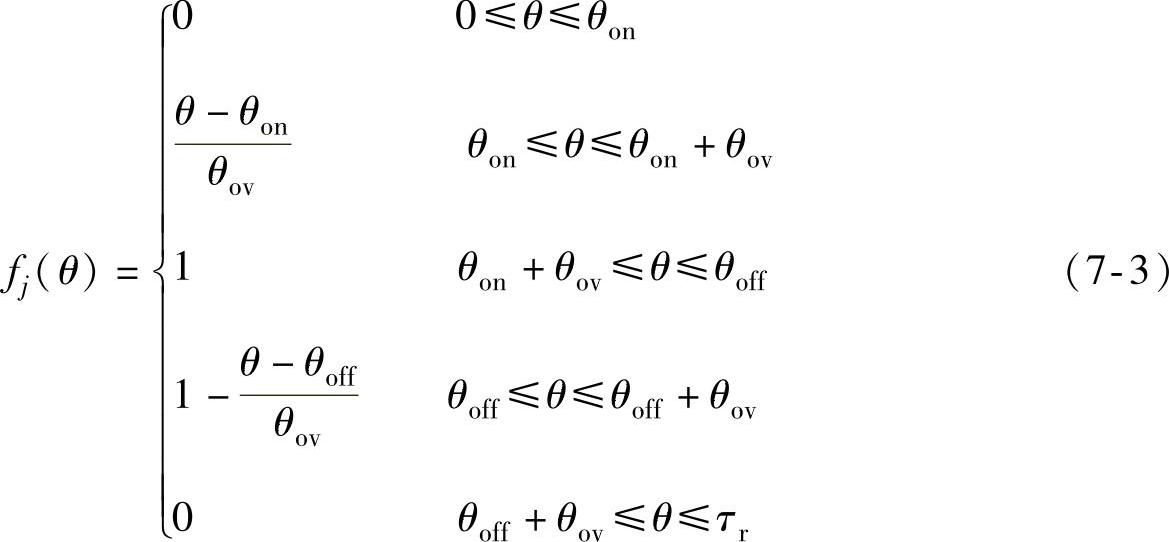
式中，θ_on为开通角；θ_off并非指常规斩波控制方式下的关断角，而是原导通相按TSF所设定规律开始减小电磁转矩的起始位置角；θ_ov为相邻两相电流重叠的角度，其应满足下式要求：

其余相的转矩分配函数的形状与j相一致，只是依次错开一个步进角。式（7-3）表明，在换相期间，相邻两相的转矩均随转子位置角θ线性变化，导通相的转矩线性增加，关断相的转矩则以相同的比率线性减小，以保证合成瞬时转矩恒定。而在非换相区，仅有一相通电并提供恒定转矩T_ref。

2.指数型TSF

如图7-1b所示，在一个转子角周期τ_r内，第j相转矩的指数型分配函数为(www.xing528.com)

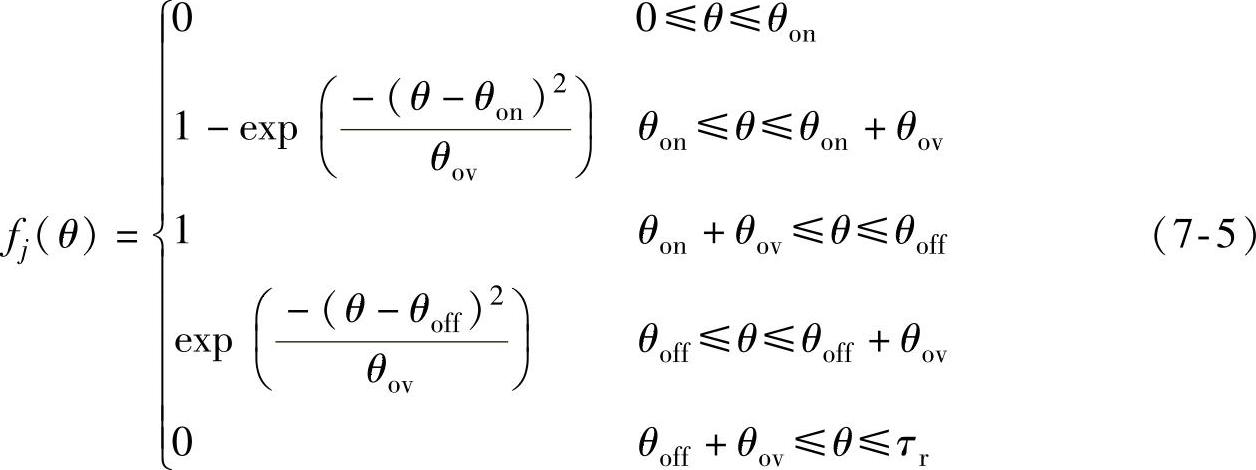
3.正弦型TSF

如图7-1c所示，在一个转子角周期τ_r内，第j相转矩的正弦型分配函数为

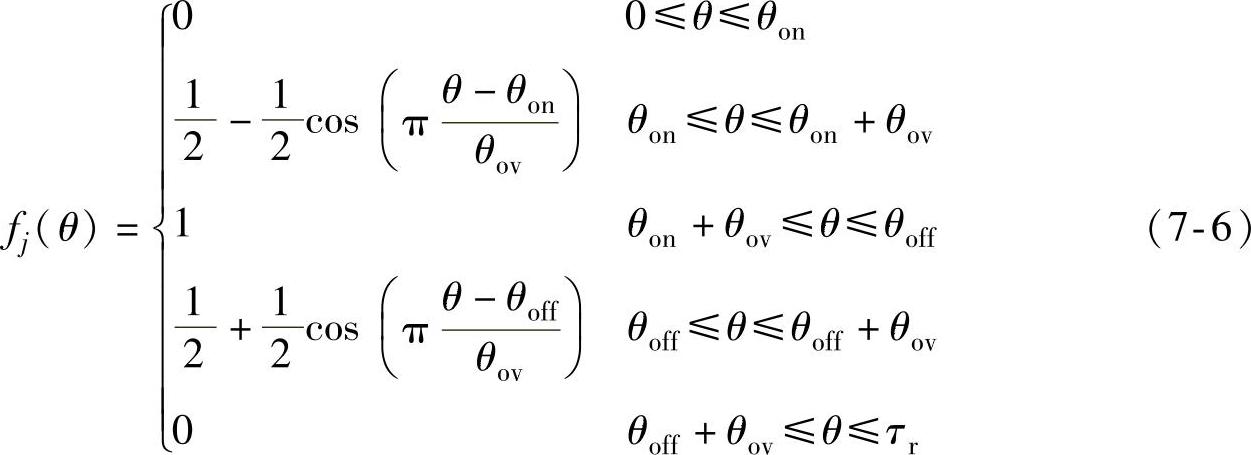
4.立方型TSF

如图7-1d所示，在一个转子角周期τ_r内，第j相转矩的立方型分配函数为

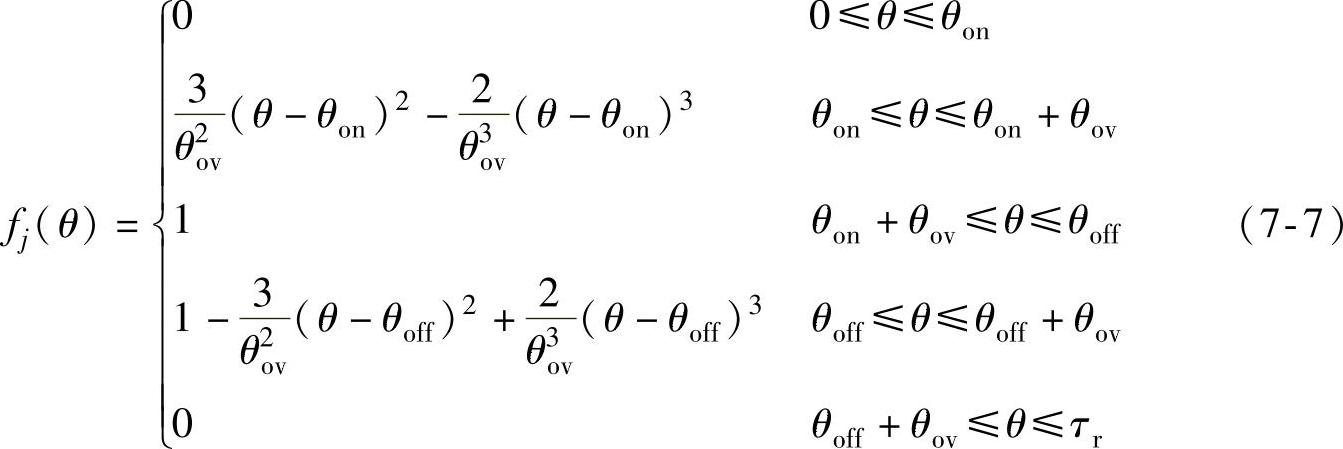
TSF是开通角θ_on、相电流重叠角θ_ov的函数。在一定的指令转矩下，θ_on、θ_ov对TSF法适用的转速范围、最高转速及SRD的效率均有显著影响，因此优化TSF设计是提高系统性能的关键。研究表明^[201]：上述四种TSF均可应用于转矩脉动最小化控制。若仅以最大转速范围为优化目标，指数型TSF最佳，正弦型、立方型TSF次之，直线型TSF对应的速度范围最小；若仅以最小铜耗为优化目标，四种TSF均可选用；当优化目标包括最大转速范围和最小铜耗时，在满足速度范围要求的前提下，优选正弦型、立方型TSF，否则指数型TSF是最佳选择。

根据TSF确定各相在不同位置处的期望转矩后，一般采用电流闭环或转矩闭环实现期望转矩跟踪的转矩脉动控制，如图7-2所示。

图7-2a中，速度控制器输出SR电动机所需的合成参考转矩T_ref，根据当前转子位置θ由转矩分配函数得A、B、C相对应的期望转矩T_Aref、T_Bref、T_Cref，并由SR电动机转矩逆模型i（T，θ）生成使瞬时转矩跟踪T_ref的期望相电流i_Aref、i_Bref、i_Cref，然后通过CCC或电压PWM控制相电流跟踪期望电流，实现转矩脉动最小控制。其中，转矩逆模型在忽略SR电动机饱和非线性的条件下，可由其简化线性模型式（1-10）推出，即

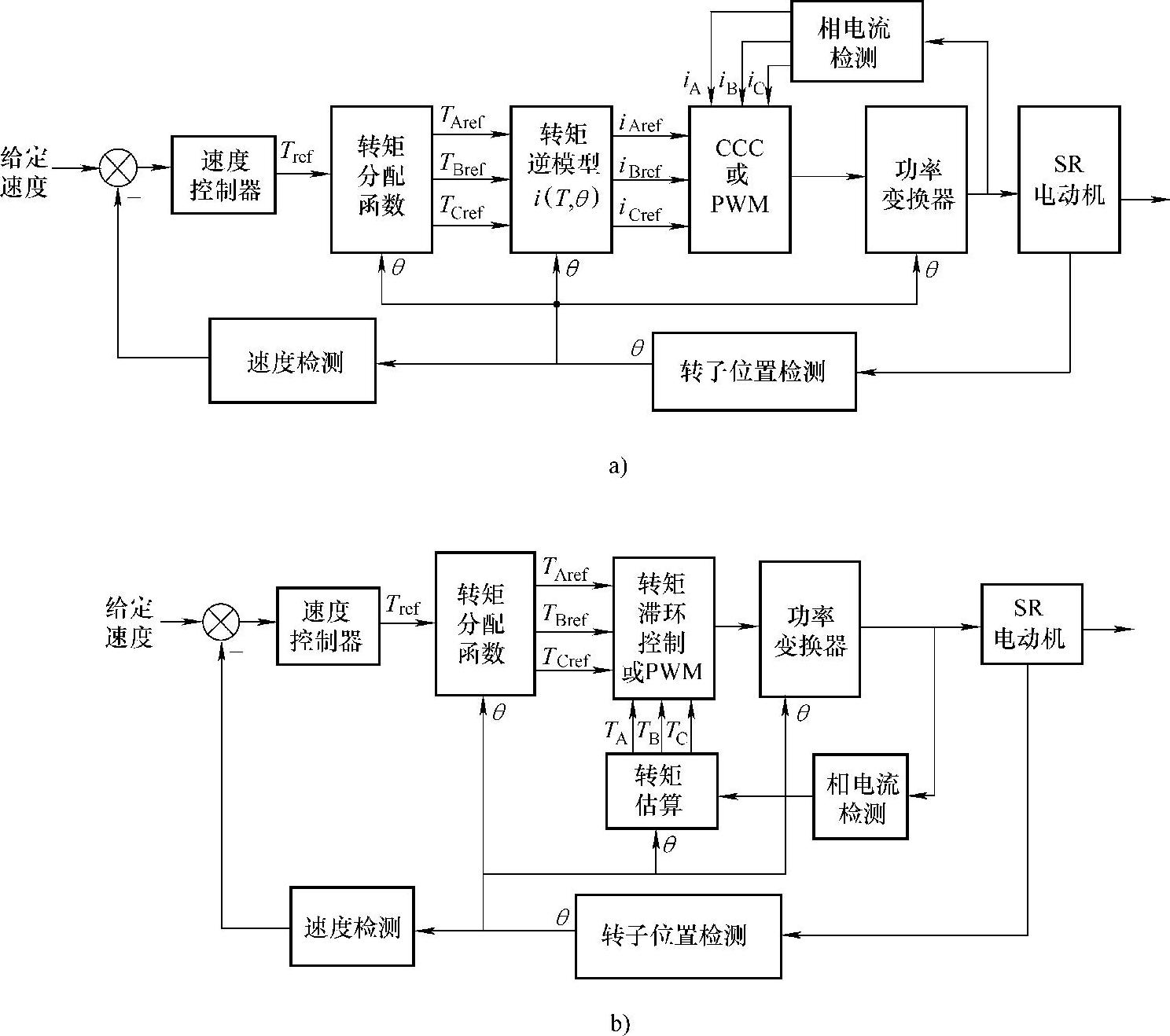
图7-2 基于TSF法的转矩脉动控制系统结构框图（以三相SR电动机为例）

a）采用电流闭环对转矩间接控制 b）采用转矩闭环的直接瞬时转矩控制

由于SR电动机实际存在严重非线性，因此式（7-8）所示的转矩逆模型尽管具有简单的优点，但误差较大，应用受限。实际应用中，可在离线静态测试或有限元计算SR电动机非线性转矩特性T（θ，i）的基础上，通过插值或人工神经网络等技术建立其非线性的转矩逆模型i（T，θ）。

图7-2b中，直接瞬时转矩控制的优点在于采用转矩闭环控制取代了电流闭环控制，无需建立转矩逆模型，实现简单。其转矩反馈信号可通过检测的转子位置θ和相电流信号插值查T（θ，i）数据表或T（θ，i）的人工神经网络模型获得。