深入探讨速度环动态特性

校正后速度环开环传递函数为

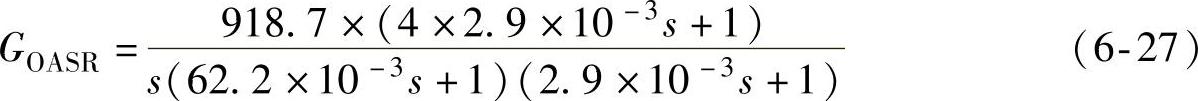
校正后的速度环及其伯德（Bode）图如图6-9所示。由此可求得其中频宽度h=ω₃/ω₂=4T_∑/T_∑=4，剪切角频率ω_cn=171rad/s，相位稳定裕度P_m=42.2°，中频衰减宽度b=ω₃/ω_cn≈2，这说明设计的SR电动机PWM调压调速系统具有良好的稳定裕度和较宽的带宽。但由于校正后的速度环为三阶系统，其时域动态性能指标与频域性能指标之间不存在准确的解析关系，可采用面向微分方程的数值仿真方法分析速度环的动态性能。

由图6-9a，若不计速度给定滤波及反馈滤波，可建立系统的能控标准型状态空间表达式为

式中，F=A-BK_nC，其中速度反馈系数K_n=0.028V/（rad/s）；B、C、A为系数矩阵，有

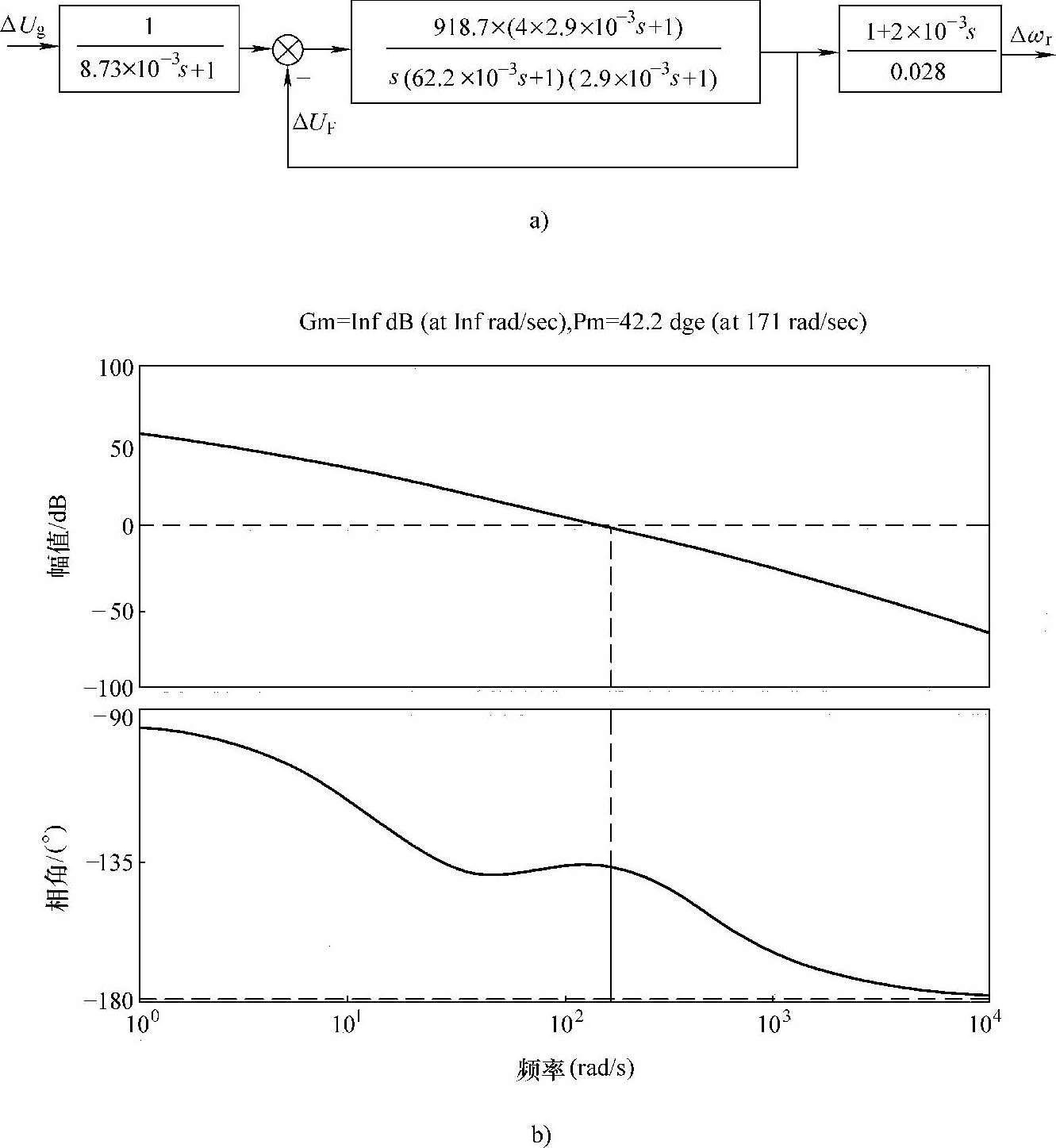
图6-9 校正后速度环动态特性

a）校正后速度环 b）校正后速度环伯德图(www.xing528.com)

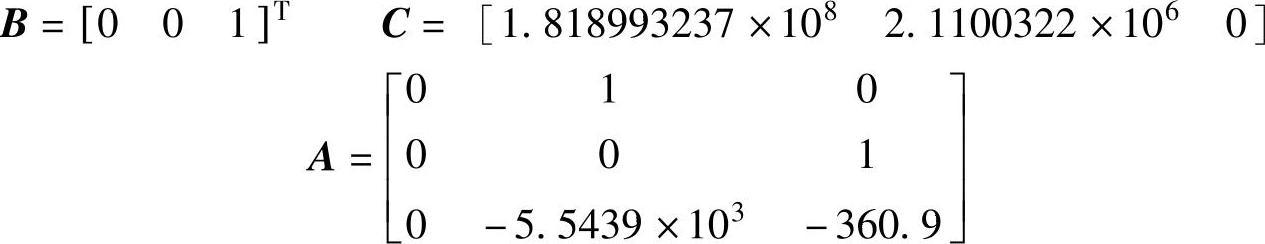
而加入T_g=8.73ms的给定滤波器后，系统输出/输入传递函数为

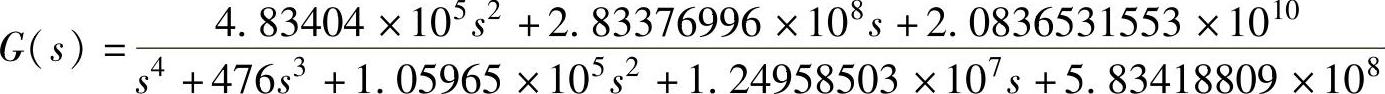
由上式可得加入给定滤波器（T_g=8.73ms）后，系统的状态方程和输出方程为

式（6-28）、式（6-29）分别构成无给定滤波器和有给定滤波器（T_g=8.73ms）作用的系统仿真模型（不包括负载）。运用龙格-库塔法等数值积分方法分别求解式（6-28）、式（6-29）可仿真分析校正后速度环不加给定滤波和加入给定滤波的动态特性。事实上，加入给定滤波后，系统的超调将明显得到遏制。对图6-5所示的SRD，给定滤波器的设计是重要的，因为若无给定滤波器，系统在起动、调速过程中的大给定量作用下，必产生饱和超调，而给定滤波器的物理意义是将给定量作平滑滤波后再送入系统，因此并不影响闭环系统的稳定性和抗扰能力，它只起延迟给定量作用，特别对压低超调有显著作用，当然亦会延缓过渡过程。如图6-8所示，整定好的调节器滤波时间常数T_g=34.92ms。

应该指出，实际SRD是非线性、时变、强耦合系统，SRD小信号动态模型是其微偏线性化模型，只有在稳态工作点附近的“小信号”范围内才有足够的精度，因此基于SR电动机小信号线性化动态模型的速度环仿真并不适用于系统大范围起制动时动态响应性能的分析计算，但其可为调节器的初步设计和系统实际运行下调节器的整定提供一定的理论指导。