量化因子与比例因子的调整方法

量化因子α_E、α_EC和输出比例因子α_U对SR电动机模糊控制系统的动、静态性能有较大的影响，应当通过系统实际运行，权衡稳、快、准三方面的要求整定。

5.4.2.1 偏差e量化因子α_E的选取

偏差e量化因子α_E的大小本质上反映了控制系统对速度偏差的分辨率，影响系统的静态误差的动态调整时间。α_E大，系统上升速率大；但α_E过大，将使系统产生较大的超调，从而延长过渡过程。若α_E很小，则系统上升慢，快速性差，稳态准确度低。

若设与第k次执行速度环对应的速度偏差量化值为E（kT），其准确量为e（kT），则有

E（kT）=INT（α_Ee（kT）+0.5） （5-78）

模糊控制系统的稳态过程可用下述模糊规则描述：若偏差为“零”，偏差变化为“零”，则控制增量为“零”。语言值“零”对应于一定的范围，当误差和误差变化都进入语言值“零”所对应的范围时，系统即进入稳态。由式（5-8）可导出误差的稳态取值范围为

则有

式（5-80）表明，稳态误差与α_E成反比。

5.4.2.2 偏差变化量化因子α_EC的选取(www.xing528.com)

α_EC反映误差变化率，其合理选择对抑制超调有显著作用。α_EC越大，系统上升速率越小，系统响应越慢，过渡过程时间长；若α_EC越小，则系统响应越快；但α_EC取值过小易导致很大的超调和振荡，这同样使系统调节时间变长。

5.4.2.3 控制输出比例因子α_U的选取

α_U在系统响应的上升和稳定阶段有不同的影响。在上升阶段，α_U取得越大，上升越快，但易导致超调；α_U小，则系统的响应缓慢。在稳定阶段，α_U过大会引起振荡，从而导致调节时间增大。

5.4.2.4 比例因子自调整模糊控制器设计

上述分析表明，模糊控制同常规控制一样，其动、静态特性之间存在一定矛盾。对于具有非线性、变结构特征的SRD，正如采用固定参数的PID控制难以获得满意的动、静态性能，采用固定参数模糊控制器也不能保证系统的动、静态性能在大范围内始终优良。因此，为改善模糊控制器的性能，需根据系统的误差和误差变化等信息对控制器的参数进行在线修正。若同时调整α_E、α_EC和α_U这三个参数会使控制算法过于复杂，大大减弱控制系统的实时性。从控制器的结构可见，比例因子α_U的大小直接影响输出量，而且最终也能起到调整α_E、α_EC的作用。因此，可选择离线整定α_E、α_EC，在线调整α_U的方法来改善系统的动、静态性能。

调整规则是：当E和EC较大时，控制系统主要是减小误差，加快动态过程，应取较大控制量，即应增大α_U；当E和EC较小时，系统将接近稳定值，这时应减小α_U，使控制量的阶跃变化小，最终达到稳态误差小的要求。由此经离线模糊推理运算，结合系统实际运行调整，得到比例因子α_U取值在线查询表，见表5-4。

表5-4 比例因子α_U取值在线查询表

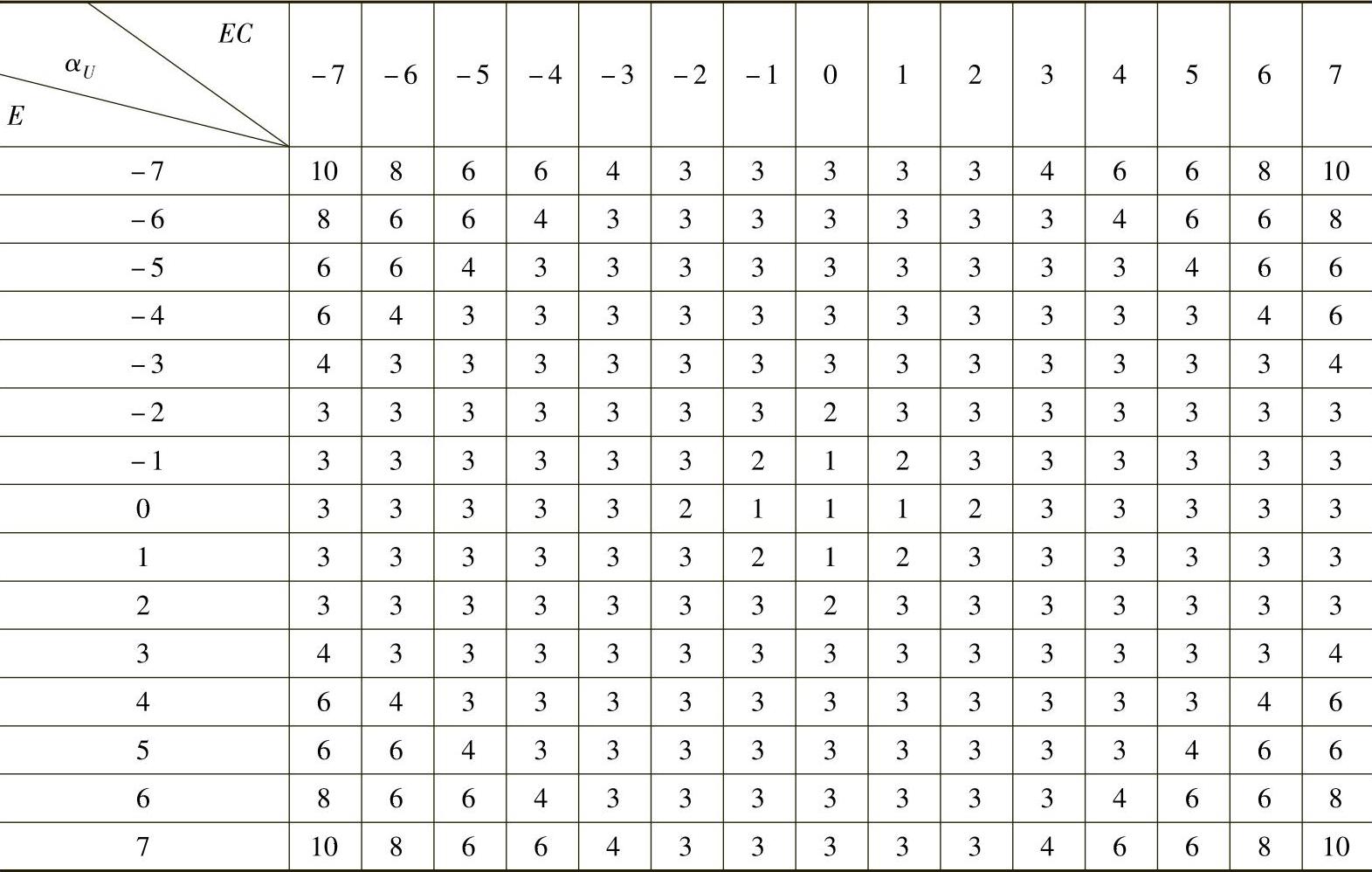
对实验样机，偏差及偏差变化量化因子离线整定为α_E=0.0175，e的约束区间为[-400，+400]；α_EC=0.035，的约束区间为[-200，+200]。

按照上述设计的SR电动机比例因子自调整模糊控制系统负载运行表明，系统有优良的动、静态特性和抗负载扰动性能^[83]。