相电流i、开通角θon、关断角θoff是SR电动机的主要控制参数。其中，相电流i的大小可由θon及θoff来调节，i的幅度变化范围为0＜i＜Im，最大值Im由主开关器件的最大允许电流值决定，SRD运行时，Im可通过电流斩波控制方式加以限制。因此，θon及θoff是SRD的主要控制变量。对一定的转速和转矩，θon、θoff可有不同的组合，故存在最优选择θon及θoff的问题。一般而言，若通过调节θon、θoff使SR电动机在一定转速时输出功率最大（即电磁转矩最大）、效率最高，则SRD即获得了角度最佳控制。
由于SR电动机及功率变换器的非线性，SRD控制参数的优化设计是一个颇为复杂的问题，必须建立SRD的非线性数学模型，对其实际的工作状态进行准确的数值仿真，从而计算出角度最佳控制的范围。
另一方面，SRD的参数优化并非一个单目标优化问题，而是一个需要考虑多种因素约束和影响的综合参数选择问题。例如，对四相（8/6）SR电动机，需要考虑如下约束条件：
（1）变量取值的限制条件
0°＜（θoff-θon）≤30° （5-42）
（2）系统运行的稳定条件 如5.2节所述，θon、θoff的选择应使Kω＞0[见式（5-6）]，以保证SRD运行稳定。
（3）转矩的连续性及减小转矩脉动的条件 电流脉冲的宽度一般不小于15°。
（4）降低振动和噪声的条件 θoff应尽可能小。
5.3.2.1 基于非线性模型的开关角优化[67]
在2.7.4节所述的基于非线性模型的SR电动机APC方式稳态运行仿真的基础上，可通过数值积分求一定角速度ωr下的平均电磁转矩Tav和相电流的有效值Iph，则SR电动机输出功率P2和绕组损耗（铜耗）Pcu分别按以下两式计算：
式中，m为SR电动机的相数；Rph为相绕组的电阻。
若忽略其他损耗，则SRD的效率η为[67]
式（5-45）表明，在不计其他损耗时，可近似认为效率与P2/PCu同时达到最大值。
选择一组θon、θoff，可仿真计算一定角速度ωr下的输出功率P2和绕组损耗（铜耗）PCu，进而可确定角度最佳控制范围。图5-9为样机1以APC方式稳定运行在157rad/s下，对应不同θon、θoff时输出功率P2及输出功率P2与绕组铜耗PCu之比（P2/PCu）的仿真曲线。由图5-9可见，对应某一开通角θon均存在一个使输出功率P2获得最大值的最优关断角θoff∗（样机1的θoff∗在22°～23°间），而且在接近P2有最大值时的θoff∗附近（在19.5°～22°间），P2/PCu亦获得了最大值。因此通过优化选择关断角使之在θoff∗附近，则无论开通角θon如何变化，SR电动机均能运行在输出功率和效率达到或接近最大值的状态。事实上，实际应用中，为简化控制，可将关断角θoff控制在最优范围内，通过调节开通角θon实现调速。如前所述，θon的选择受系统最大允许电流和稳定性的限制。在某一速度下，θon前移越多，则电流峰值越大。当电流达到上限值时，因对电流的限幅斩波作用会引起电磁转矩突降，导致系统不平稳。所以在一定速度下，当θon超出其允许变化范围时，就要对θoff进行调节。
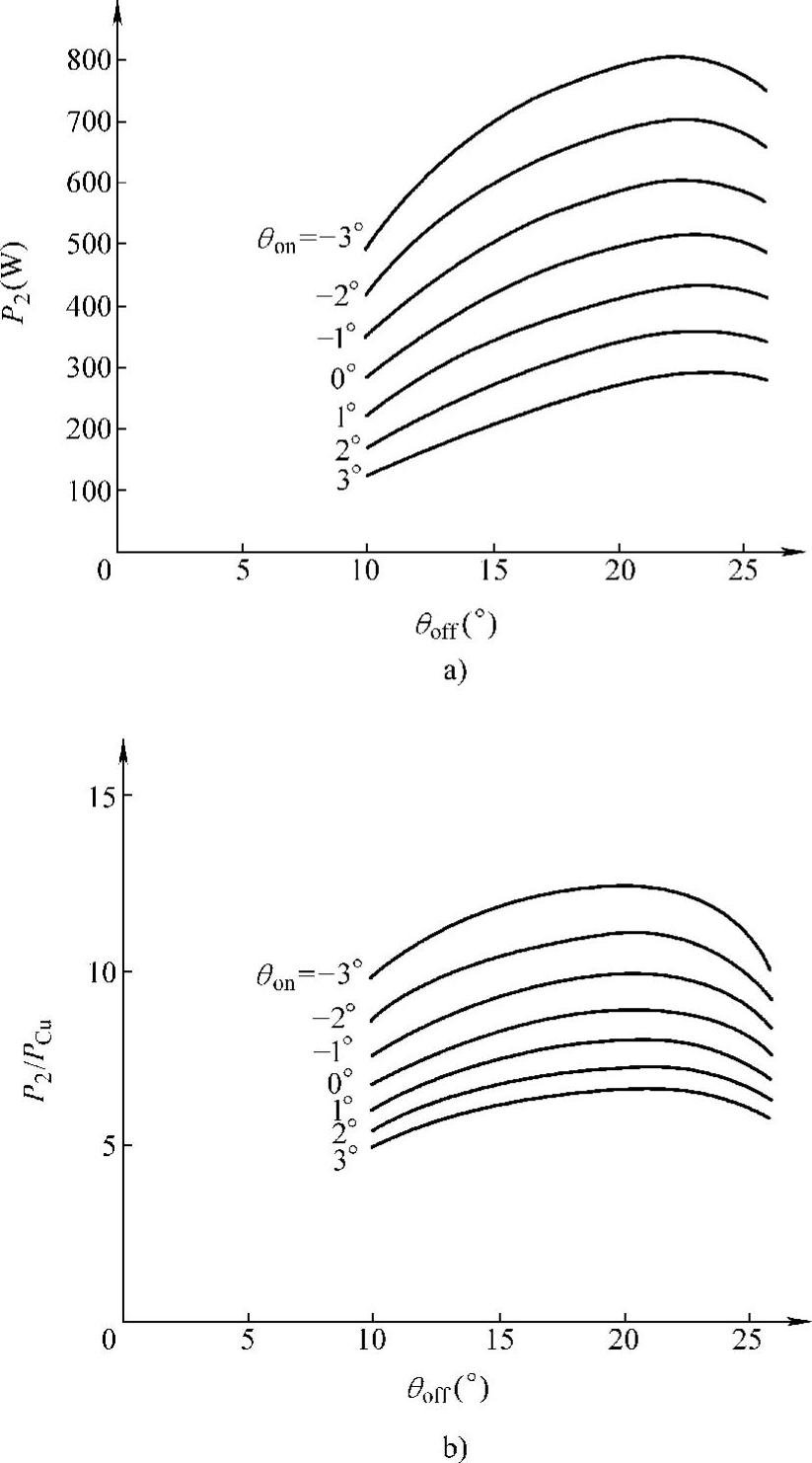
图5-9 样机1以APC方式稳定运行在157rad/s时的仿真结果
a）输出功率P2随开关角变化的曲线 b）P2/PCu随开关角变化的曲线
5.3.2.2 基于线性模型的关断角优化[68]
上面应用龙格-库塔数值积分方法求解SR电动机非线性微分方程式（2-84），仿真研究了开关角优化，具有精度较高的优点，但计算较复杂。为简化计算，参考文献[68]基于SR电动机线性模型，以在一定电流幅值下输出转矩最大为优化目标研究了APC及CCC方式下关断角的优化控制。
图5-10所示为SR电动机线性模型及APC方式下相电流波形，其是基于关断过程在电感上升区开始、在电感下降区结束的假设画出的，即θoff≤θ3，θz≥θ4，且为方便起见，将角度位置的参考零位设在θ2处。在2.3.3节，基于SR电动机线性模型对相电流进行了解析分析，但这些关系式均与角速度ωr有关，为使电流波形的解析式具有通用性，参考文献[68]以与θon=θ2-Lminβs/（Lmax-Lmin）对应的平顶波电流
为电流基值，以定子极弧角βs为角度基值，定义电流标幺量为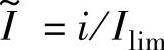
，角度标幺量α=θ/βs，并设绕组励磁阶段的外加电压为Us，主开关器件关断后续流阶段所加电压为-Us，得图5-10所示相电流标幺值的分段解析式[68]。
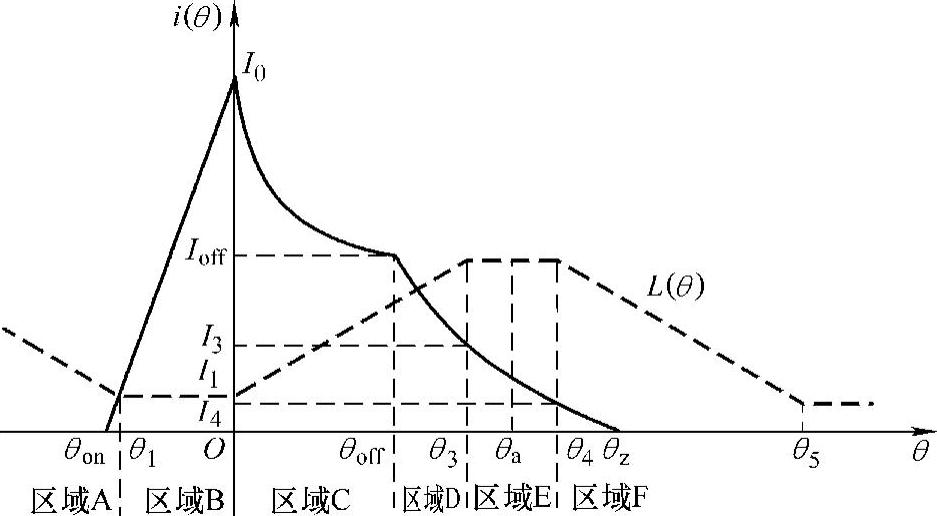
图5-10 APC方式下典型相电流波形（基于线性模型）
区域A：
区域B：
区域C：若为APC方式，即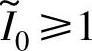
，则
若为CCC方式，即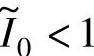
，则
区域D：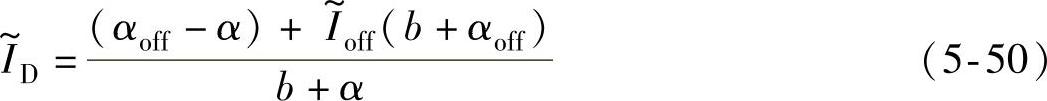
区域E：
区域F：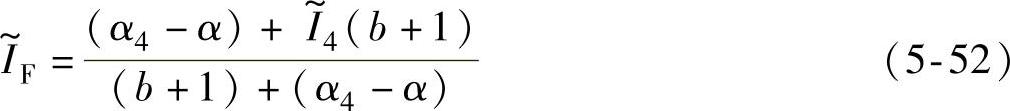
式中，b为电感比率，b=Lmin/（Lmax-Lmin）；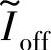
为关断起始的相电流；
、
、
、
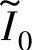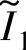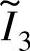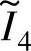为与电感分布曲线不同区域边界对应的相电流，即
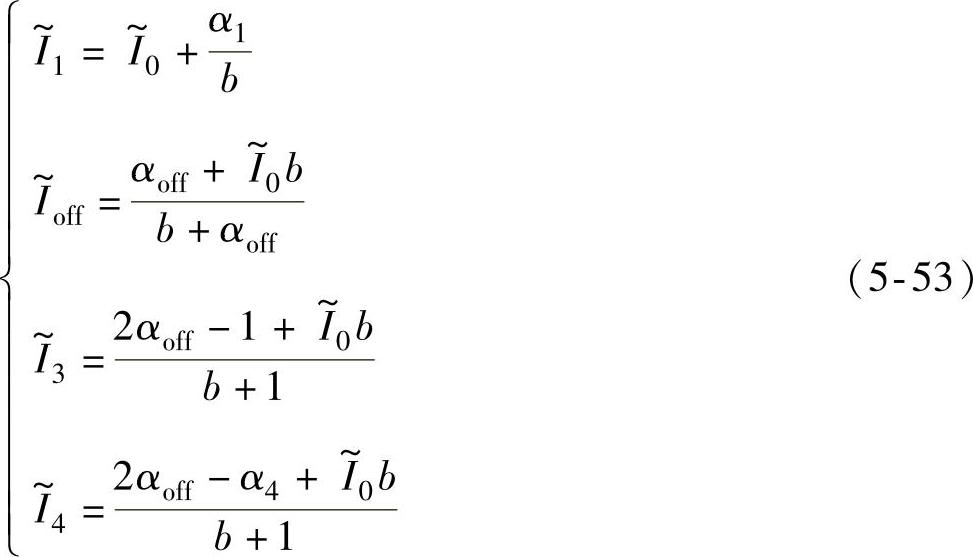
令式（5-52）中的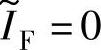
，得相电流衰减至零的位置角αz为
则关断过程所占角度αp为
式（5-54）及式（5-55）表明，若电感比率一定，αz和αp仅取决于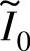
和αoff；而式（5-47）、式（5-48）表明，开通角标幺值αon与
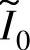一一对应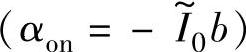
。
当采用图5-10所示位置参考坐标系时，样机1的不饱和电感分布曲线参数为：Lmax=0.1403H，Lmin=0.0087H，θ1=-16°，θ2=0°，θ3=21°，θa=22°，θ4=23°，θ5=44°，电感比率b=Lmin/（Lmax-Lmin）=0.0661，特殊位置角标幺值为：
α1=-0.7619，α2=0，α3=1，αa=1.0476，α4=1.0952，α5=2.0952
利用式（5-47）～式（5-52）可计算SR电动机在不同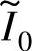
和αoff下的相电流及转矩[参见式（2-38）中，当i＜i1时所对应的转矩计算]，进而可分析αoff对输出转矩的影响。图5-11所示为样机1的仿真结果。(www.xing528.com)
由图5-11可见，当以输出转矩最大为优化目标时，随着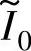
从1增加到8，αoff的最优值则从0.78减小到0.65，若αoff选择不当，将导致输出转矩显著降低。图5-11中，与
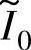从8减小到1对应，开通角标幺值
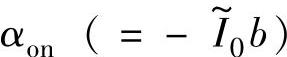由-0.5289增大至-0.0661，实际开通角θon由-11.1064°增大至-1.3883°（若转换至以定子凸极与转子凹槽中心重合位置为参考零位的坐标系，则为由-3.1064°增大至6.6117°），最优关断角θoff∗则由13.65°增大至16.38°（若转换至以定子凸极与转子凹槽中心重合位置为参考零位的坐标系，则为由21.65°增大至24.38°），这一结果与5.3.2.1节基于非线性模型的开关角优化结果接近。
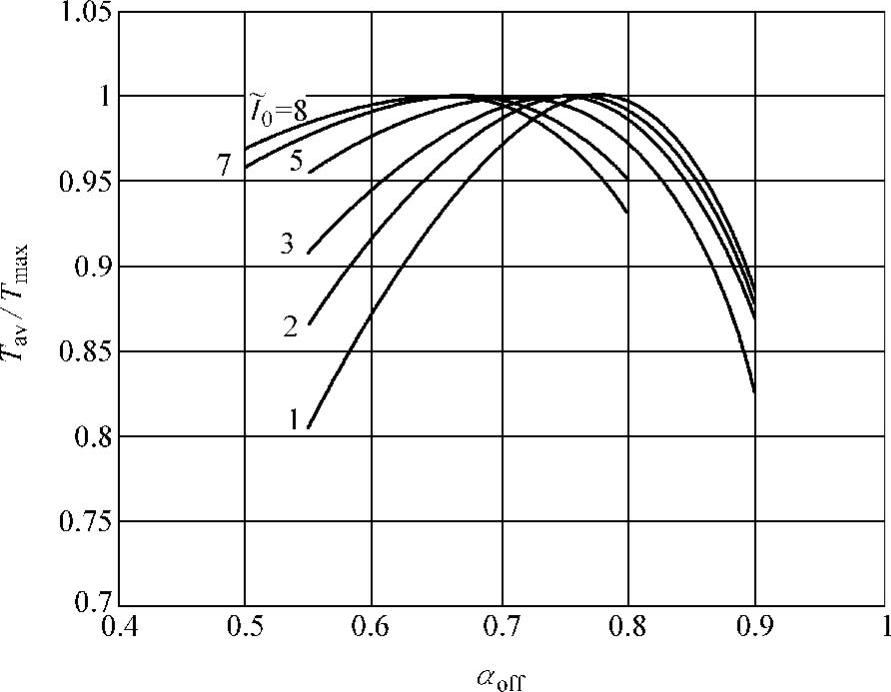
图5-11 样机1在不同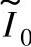
和αoff下，平均转矩与最大转矩之比
为找到以输出转矩最大为优化目标的关断角最优控制规律，参考文献[68]引入“关断比率αKom”的定义，以度量定、转子凸极重合位置θa后续流过程所占角度与整个关断续流过程所占角度αp的比值大小，即
为确定最优的关断比率值，应计算以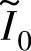
和αoff为自变量的有效输出转矩，即
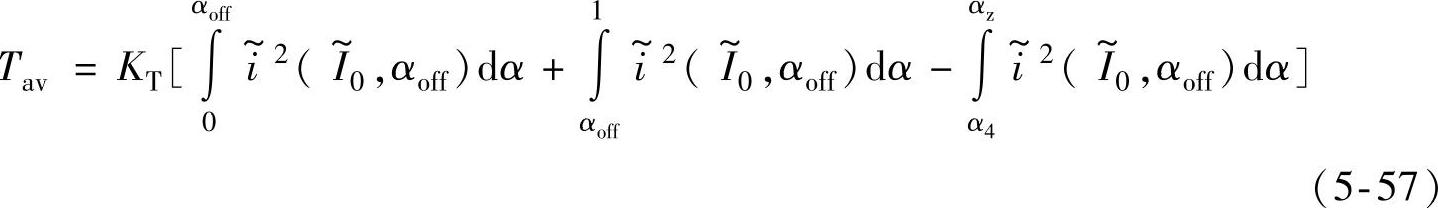
式中，KT为由不饱和电感分布曲线所确定的常数，KT=（Lmax-Lmin）Nr/（4π）。则最优的关断比率为
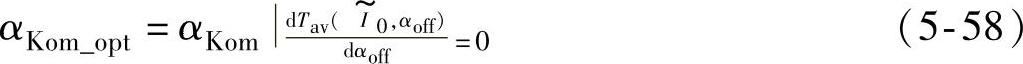
式（5-57）和式（5-58）无解析解。参考文献[68]针对b=0.187、αa=1.0935的样机，用数值求解方法求得当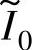
从10减小至1，αKom_opt由0.63增大至0.69，且αKom的最优值与SR电动机的相电感参数b、α4无关。因此，对所有的
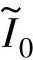，αKom=2/3均是优化的选择，即
分析表明[68]，若关断比率αKom按式（5-59）选择，当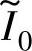
变化时，输出转矩的最大降落将小于1%。
将式（5-59）和式（5-54）代入式（5-56），得APC方式最优关断角的算法为
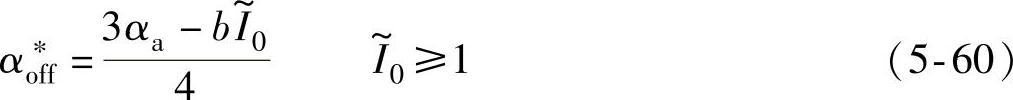
将样机的相电感参数b=0.0661及αa=1.0476代入式（5-60）可推出样机1最优关断角与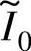
的关系为
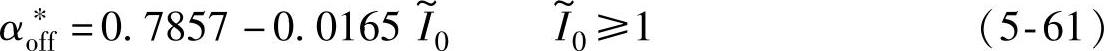
将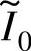
的值分别代入式（5-61），求出的最优关断角αoff∗与图5-11的数值仿真结果能良好吻合，表明式（5-60）所示的关断角最优控制算法有效。
采用变角度电流斩波控制方式的最优关断角算法与APC运行时最优关断角算法相似。CCC方式运行时，电流控制器通过控制相电压的平均值，实现平均的di/dt=0，从而使相电流平均值维持在期望值。根据式（2-4），忽略相绕组电阻上的压降，得CCC方式下的电压方程式为
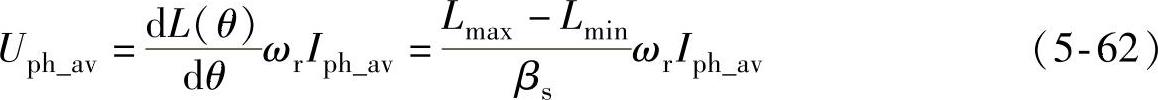
式中，Uph_av、Iph_av分别为通电相绕组端电压平均值和电流平均值。
将式（5-62）所示的平均电压Uph_av与外施直流电源电压Us相比较，定义电压比例因数Ka为
又根据式（5-46）所示的斩波控制方式和APC方式转换的阈值电流Ilim表达式，得
将式（5-64）、式（5-62）代入式（5-63），得
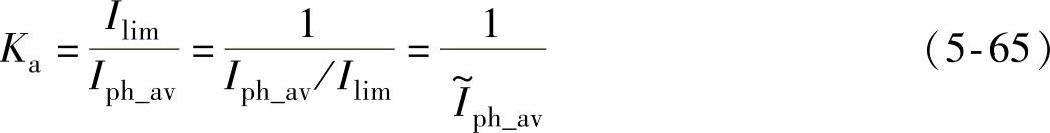
式中，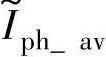
表示以Ilim为基值的通电相绕组电流平均值的标幺值。
对CCC方式而言，关断起始时的电流与电感开始上升处（即θ=θ2处）的电流相等，即
而CCC方式在位置角θ3、θ4处的相电流标幺值分别为
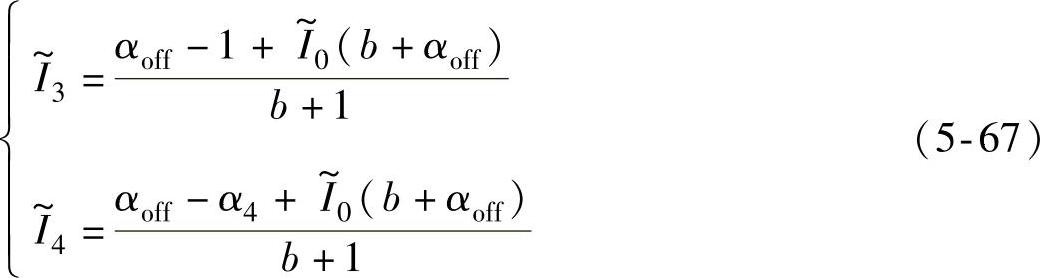
则令
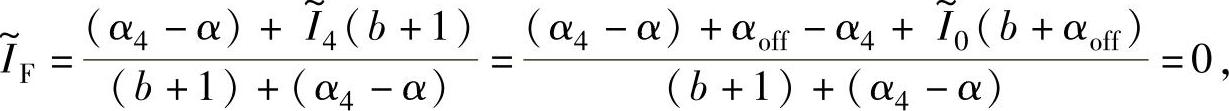
得CCC方式下相电流衰减至零的位置角αz为
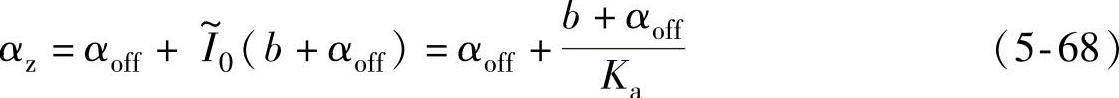
将式（5-68）代入式（5-56），整理得CCC方式下与关断比率αKom对应的关断角标幺值为
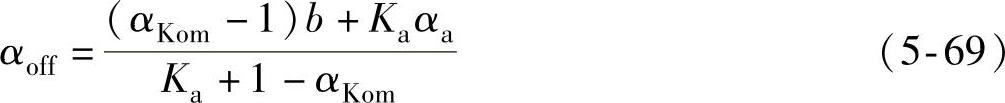
在一定的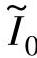
下，若αoff=1，且续流电流在电感下降区前衰减至零，即αz≤α4，则可获得最大输出转矩，由式（5-68），CCC方式下满足这一条件的最大允许
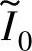值为
对样机1，将已知参数α4、b代入式（5-70），得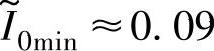
，这意味着若
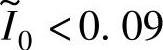，则最优关断角标幺值αoff∗=1。
若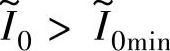
，研究表明[68]CCC方式的关断比率最优值与APC方式基本相等，故仍可取αKom_opt=2/3，代入式（5-69），且由
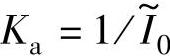，得CCC方式下最优关断角的算法为
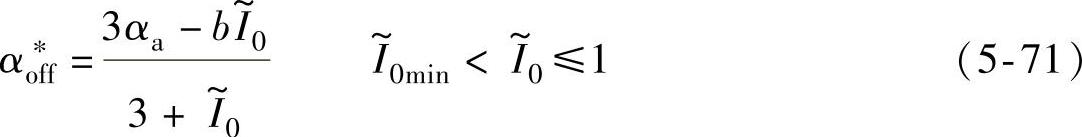
比较式（5-60）与式（5-71）可见，在CCC和APC两种控制方式下切换点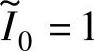
处，最优关断角的解是连续的。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
