调节器设计方法：二阶最佳工程设计

类似于式（5-23）的推导过程，在不同运行条件下，SRD速度调节器的调节对象传递函数皆可近似等效为下式所示的形式，即为时间常数不同的两个惯性环节：

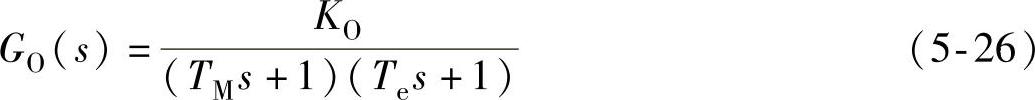
式中，T_M＞T_e。

本节主要讨论SRD速度调节器的工程设计方法。

5.2.2.1 “二阶最佳”工程设计方法

按“二阶最佳”工程设计方法，对式（5-26）所描述的调节对象，调节器应采用PI调节器，即

使（τ₁s+1）与调节对象的大惯性环节对消，即

τ₁=T_M （5-28）

并选择T_i满足

T_i=2K_OT_e （5-29）

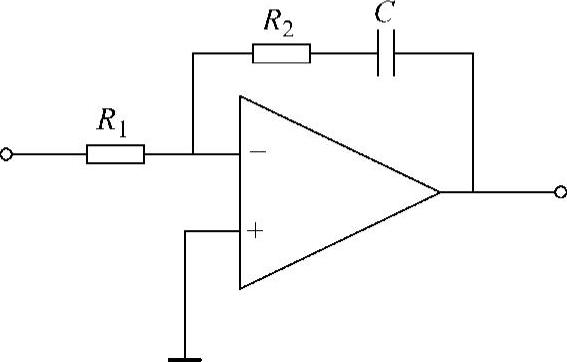
图5-5 PI调节器电路

“二阶最佳”设计中的PI调节器可用式（5-27）～式（5-29）作为依据，按图5-5设计具体的PI调节器电路。

图5-5中元件参数按下式选择：(www.xing528.com)

5.2.2.2 “三阶最佳”工程设计方法

SRD一般并不满足T_M≥30T_e的条件，但实践证明，当T_M＞T_e时，一般仍可将T_M惯性环节近似视为积分环节来计算“三阶最佳”设计的调节器，即对式（5-26）的被控对象采用式（5-31）所示的PI调节器，即

式中，τ₁=4T_e （5-32）

T_i=8K_OT_e²/T_M （5-33）

“三阶最佳”设计中的PI调节器可用式（5-31）～式（5-33）作为依据，按图5-5设计具体的PI调节器电路。

5.2.2.3 调节器设计小结

对SRD，无论是按“二阶最佳”工程设计方法设计，还是按“三阶最佳”工程设计方法设计，都采用PI调节器，其结构相同，只是调节器参数的设计方法不同。

众所周知，二阶设计超调量小，系统稳定性好，在阶跃输入时的静差为零，斜坡输入时的静差为常数，系“Ⅰ”型系统；三阶设计的优点是当无给定滤波器时，阶跃输入静差及斜坡输入静差皆为零，属于“Ⅱ”型系统，但没有给定滤波器的三阶设计超调量一般达43%，稳定性较差。加了给定滤波器虽可减小超调量，但在斜坡输入时存在静差，而且过渡过程时间较长。

作者认为：SRD速度环调节器设计以选“三阶最佳”工程设计方法为宜，理由如下：

首先，在SRD中，T_M＞4T_e的条件是满足的，而这时三阶克服阶跃扰动所需的恢复时间就远小于二阶；其次，同样的PI调节器，二阶的时间常数τ（=T_M）和SR电动机的机电时间常数有关，这不但要临时进行测量、计算，而且不易准确测量、计算。而三阶的τ（=4T_e）和小惯性群等效时间之和有关，这些参数是由SRD的功率变换器、斩波放大器、速度反馈环节等决定的，一般较易计算或预先实测出，不必在现场调试时进行测量，虽说调节对象放大倍数和大时间常数T_M初始设计时同样难以准确预知，但其影响的只是PI调节器比例增益的确定，可以先粗略估算，然后现场仅需调整PI调节器的比例增益即可权衡系统稳、快、准的要求。

以上所讨论的基于“二阶最佳”和“三阶最佳”设计方法的调节器设计是针对式（5-26）的调节对象而言的。实际的SRD要较式（5-26）复杂得多。

首先，式（5-26）是从SRD小信号动态模型作若干近似处理后得到的；其次，SRD小信号模型本身亦是近似的，只有在“小信号”下才有足够的近似精度，因此实际SRD的调节器在PI调节的基础上通常还需要加上微分（D）调节器，即构成PID调节器，由二阶、三阶设计方法所得到的调节器参数往往需要在现场调试中加以修正。事实上，SRD之所以一般选PID调节器，正是因为SRD准确的动态模型难以建立，而PID调节器的优点在于即使在被控对象模型未知的情况下，其比例、积分、微分常数亦可通过系统的实际运行进行现场整定。