SRD小信号模型及其传递函数优化

5.2.1.1 SR电动机小信号模型及传递函数

本书2.4节，以理想化非线性能量转换模型为基础，得到SR电动机的总平均电磁转矩的解析式（2-50）。式（2-50）表明：在电动机结构、电磁参数一定时，转矩为控制参数U_S、θ_on、θ_off及受控变量ω_r的函数。由微分学原理，转矩T_av的全微分方程式为

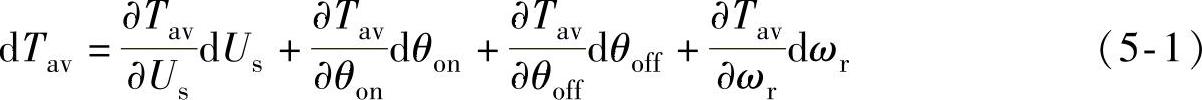
由非线性系统线性化理论，将式（5-1）中各变量微分用对应的增量代替，即得SR电动机在工作点附近小信号线性化的转矩方程为

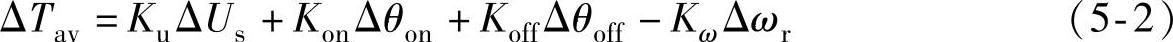
式中，K_u=∂T_av/∂U_s；K_on=∂T_av/∂θ_on；K_off=∂T_av/∂θ_off；Kω=-∂T_av/∂ω_r。

显然，随着运行方式的不同，上述各参数的表达形式亦不同。就2.4节所讨论的平顶波电流而言，由转矩方程式（2-50），可求得各系数表达式分别为

仿照式（5-2）的推导，对SR电动机机械运动方程式（2-5）也作小信号线性化处理，得到其增量形式为

考虑到SR电动机APC方式运行时，在某相导通后输入的角度控制指令要经过一转子极距角τ_r的延迟，直到该相再次导通时才被响应，所以若角度控制的输入量为Δθ～_on、Δθ～_off，则有

式中，τ为SR电动机响应角度控制指令时延平均值，一般约为几毫秒。

式（5-2）、式（5-7）和式（5-8）构成SR电动机时域小信号模型，对其分别取拉普拉斯变换，即得s域小信号模型如式（5-9）所示，即

与式（5-9）对应的SR电动机微偏线性化的动态结构框图如图5-1所示。

图5-1 SR电动机微偏线性化的动态结构框图

5.2.1.2 SRD中其他环节的传递函数

1.功率变换器传递函数

由图5-1可见，SRD共有三个控制变量输入端，即ΔU_s（或为ΔI_p）、、，与此相对应，功率变换器输出根据控制方式不同，必然有三个不同的输出分支。

（1）斩波控制方式 与ΔU_s或ΔI_p对应的分支代表系统的斩波控制方式，包括电压斩波控制，输出ΔU_s；或电流斩波控制，输出ΔI_p。

电压斩波过程可看作对调节器输出ΔU_ASR的采样过程，且具有放大倍数K_c，则脉宽调制器和功率变换器的s域小信号模型为

式中，T为斩波周期。

（2）角度位置控制方式 与图5-1所示的SR电动机小信号模型中的两个角度控制输入、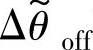对应的功率变换器通道的模型相同，角度信号通过功率变换器除延时τ_p以外，没有别的变化。

2.速度调节器及速度反馈环节的模型

一般采用PID调节器作为速度调节器，其传递函数为

G_ASR（s）=K_P[1+T_Ds+1/（T_Is）] （5-11）

式中，K_P、T_D、TI分别为比例、微分、积分常数。

速度反馈一般采用F/V电路或数字测频（M法）、测周（T法）等方法，通常可用一小惯性环节等效，即

G_ω（s）=K_n/（1+T_ωs） （5-12）

式中，K_n为速度反馈系数；Tω为测速环节时间常数。

5.2.1.3 SRD整体动态结构框图及传递函数

SRD微偏线性化的动态结构框图如图5-2所示。

图5-2中，S₁～S₃表示运行方式转换控制操作，系统运行在不同的控制方式下，则对应着不同的开关闭合及不同的系统结构和传递函数。

图5-2 SRD微偏线性化的动态结构框图

电压PWM调压调速控制时，图5-2中的S₁闭合，系统对应的开环传递函数为

式中，K_oc=K_pK_cK_uK_n/（D+K_ω）；T_M=J/（D+K_ω）。

而闭环传递函数则为

APC方式运行时，系统中包含纯滞后环节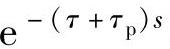。因为通常基速以上采用APC方式，故τ值一般很小，约为几毫秒。例如，四相SR电动机运行在1500r/min时，τ_max≈6.7ms。而τ_p则由功率变换器主开关器件的开关频率决定，通常为微秒级。总之，延时时间（τ+τ_p）很小，可将纯滞后环节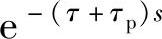近似为一阶小惯性环节，即

(www.xing528.com)

而其与小惯性环节G_ω（s）一起可用一个惯性环节等效，即

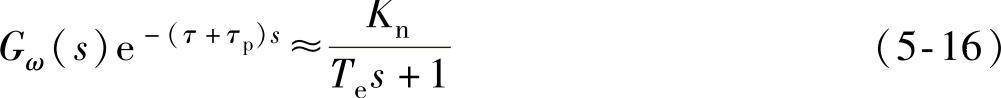
式中，T_e=τ+τ_p+T_ω。

由此得以θ_on为控制变量（S₂合上）时系统的开环传递函数，即

式中，K_OA′=K_pK_onK_n/（D+K_ω）。

其闭环传递函数为

若APC方式运行，θ_on、θ_off均为控制变量，则图5-2中的S₁、S₂同时闭合，对应的开环传递函数为

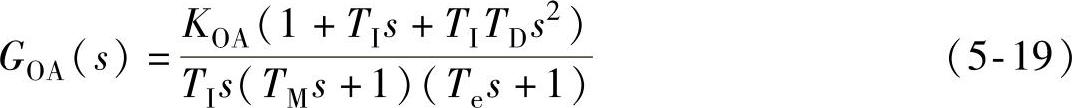
式中，K_OA=K_p（K_on+K_off）K_n/（D+K_ω）。

对应的闭环传递函数为

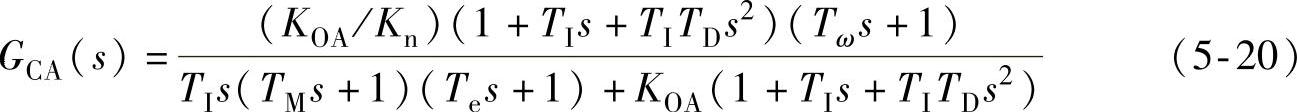
5.2.1.4 SRD的闭环控制特性

因电压PWM控制方式下的斩波频率通常选得较高，图5-2中的零阶保持器可近似用一个小惯性环节来等效，即

将式（5-21）代入式（5-13），且根据等效小惯性群理论，将T、Tω两个小惯性环节用惯性时间常数T∑=T+Tω的一个等效惯性环节代替，则电压PWM控制方式下的系统开环传递函数等效为

式中，K′_OC=K_pK_cK_uK_nT/（D+K_ω）；T_∑=T+T_ω。

CCC方式时系统的开环传递函数与式（5-22）具有类似的形式，只是系数不同。

由式（5-17）、式（5-19）和式（5-22）可见，闭环SRD在不同调速控制方式时系统的结构和传递函数不相同，但经近似等效处理后，它们将简化成具有相同的结构形式，但参数不同，即具有下式所示的同构异参开环传递函数：

由图5-2可见，在SRD闭环调速系统内部包含一个SR电动机小闭环，该小闭环的极点为

p_M=-（D+K_ω）/J （5-24）

则SR电动机动态稳定运行的条件为

K_ω＞-D （5-25）

式中，D为粘性摩擦系数，为很小的正数。

由式（5-25）可见，只要合理选择控制参数θ_on、θ_off，使K_ω＞0[参见式（5-6）]，则SR电动机稳定运行。一般来说，固定开关角的斩波控制方式和角度位置控制方式下SR电动机电动运行，其稳定条件是能够满足的。图5-3所示为样机1、样机2在APC方式时Kω随角速度ω_r变化的曲线。

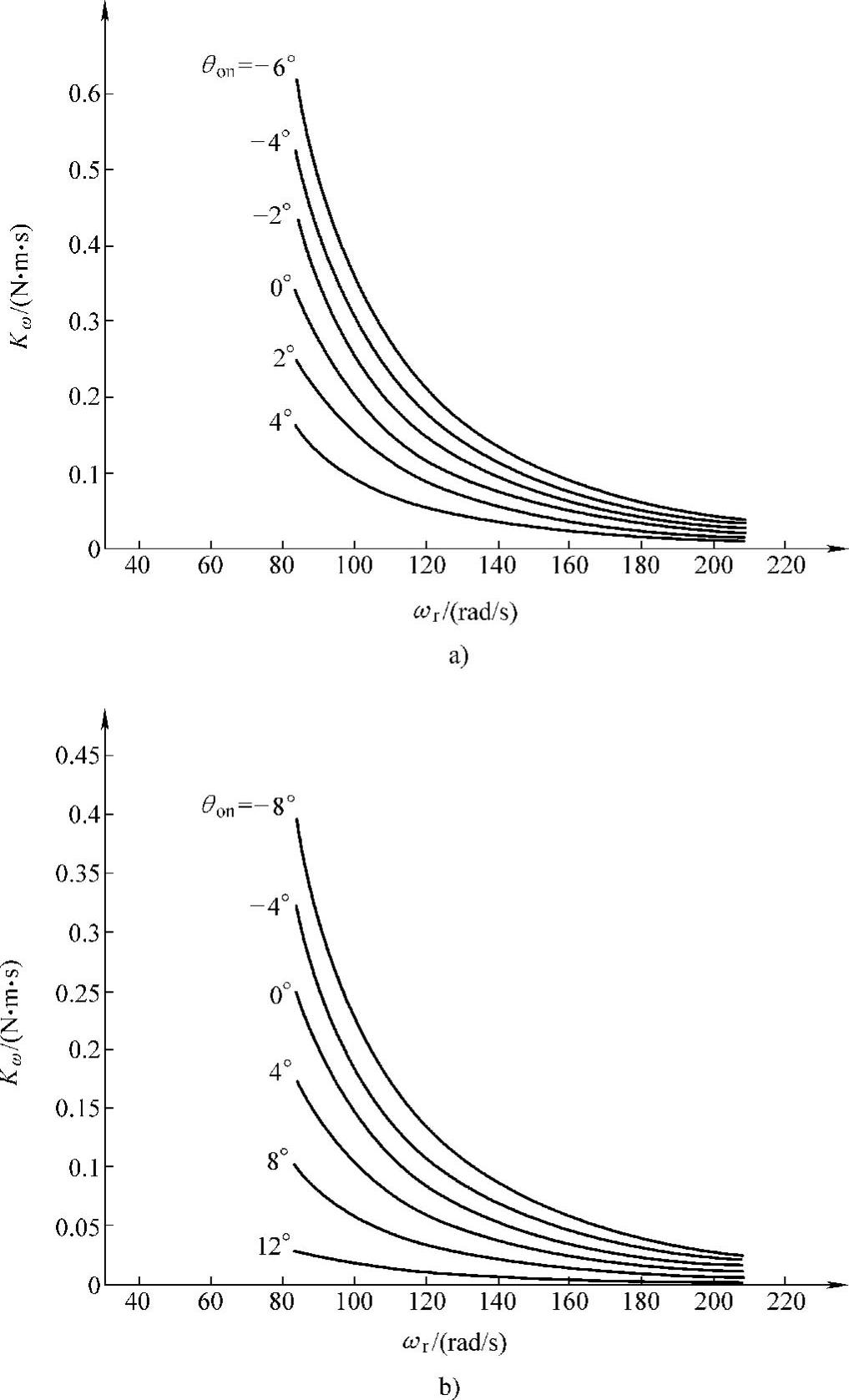
图5-3 APC方式下K_ω随角速度ω_r变化的曲线

a）样机1（θ_off=22°，θ_on=-6°、-4°、-2°、0°、2°、4°）

b）样机2（θ_off=28°，θ_on=-8°、-4°、0°、4°、8°、12°）

在分析SR电动机动态稳定的基础上，可进一步分析SRD的闭环控制特性。根据式（5-23），设PID调节器有一对共轭复数零点z₁，2=-5±j，且p₁=-1/T_M=-1，p₂=-1/T_e=-7，即系统的开环传递函数为

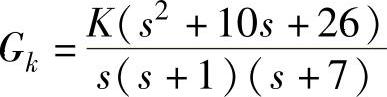
图5-4所示为对应的闭环系统根轨迹。

图5-4 SRD闭环根轨迹

由图5-4可定性地讨论闭环SRD的性能。

1.稳定性

由于当开环增益从零变到无穷大时，图5-4上的根轨迹不会越过虚轴进入右半s平面，因此，对所有K值SRD均稳定。同时，图5-4亦表明，要保证闭环系统的根轨迹位于左半s平面，必须p₁、p₂、z₁、z₂均位于左半s平面，其中p₂、z₁、z₂显然满足这一条件，而p₁=-1/T_M=-（D+K_ω）/J＜0的条件正是SR电动机稳定运行的条件式（5-25）。由此可见，只要控制SR电动机的运行参数Kω满足式（5-25），则闭环SRD稳定。

2.稳态性能

由于开环系统在原点有一极点，故系统属Ⅰ型无差系统，根轨迹上的K值即为静态速度误差系数，若给定系统的稳态误差要求，则可根据图5-4确定闭环极点位置的容许范围。

3.动态性能

当K＜K_d时（图5-4中的K_d≈0.076），闭环极点均为实数极点，系统为无超调非振荡型系统，随着K值的增大，超调、调节时间均发生变化。通过调节系统各环节的放大倍数K_n、K_u、K_on、K_off、K_p即可调节K值，进而调节闭环系统的动、静态性能。应该指出，图5-4所示的根轨迹的形状不仅与p₁、p₂值有关，而且还与由PID调节器参数决定的零点z₁、z₂的位置有关。另一方面，z₁、z₂同时亦是闭环零点，若在系统设计中，设法使其尽可能地接近闭环极点，系统性能将得到显著改善。因此，当参数随运行条件不同而变化时，只要控制PID调节器参数使零点也发生变化，即可使系统的动态性能指标始终满足一定的要求，这正是SRD变参数PID调节器设计的理论依据。