无位置传感器间接检测转子位置的方法优化

SRD引入位置传感器带来的不利因素是：增加了SR电动机结构的复杂性；增加了SR电动机与控制器之间的电路连线；增加了成本和潜在的不稳定性；而且由于传感器分辨率的限制，导致SRD高速运行性能下降。为此，出现了多种取消位置传感器的间接检测转子位置方案。这些方案大都采用监测SR电动机一相或几相绕组的电流和磁链（或电感）进行转子位置推断，分别适用于高、低转速范围内运行的SR电动机转子位置间接检测。

4.2.2.1 适用于较低速度范围内运行的转子位置间接检测方法

这类方法的共同特点是：在很短的时间Δt内，对非励磁相绕组施加检测电压脉冲，测量受检相绕组的相电感进行转子位置估算。由于检测脉冲作用的时间Δt很短，故通入受检相的测试电流Δi很小，故测得的相电感可视为不饱和电感L（θ），测试电流在受检相中产生的制动转矩以及电阻压降均可忽略，且若SR电动机的转速较低，受检相绕组的运动电动势亦可忽略，则由下式得

式中，U为检测电压脉冲的幅值；Δt为检测电压脉冲的宽度；Δi为Δt时间内受检相绕组电流的增量。

这类方法主要存在两个局限：其一，由于SR电动机相绕组间存在互感，励磁相绕组的电流对受检相的测试信号会形成干扰，从而影响测量的准确性；其二，不适合高速运行的SR电动机转子位置估算，因为高速运行时，相绕组的励磁电流通常占据了转子角周期的大半，当励磁电流尚未降为零时，若施加检测电压脉冲，将造成测试电流与励磁电流叠加而导致检测失败，另外，受检相的运动电动势在高速运行时亦不宜忽略。

这类方法的具体实现有如下几种途径：

1.基于斩波波形

即通入受检相的测试电流是偏差为Δi、平均值为i的斩波电流，由式（4-2），斩波偏差时间Δt为

式中，Δi、U均为设定值。因此，Δt与L（θ）一一对应，可将Δt与对应转子参考位置的Δt_ref作比较，当Δt超出Δt_ref这一参考阈值时，换相即开始，按序转为受检相励磁，同时其后一相开始进入检测状态。

2.基于相电感谐振

该方法早期亦称为频率调制法，即将受检相与辅助电路相连构成频率f与相电感成反比的振荡器，且利用F/V变换电路或二进制计数器将f与对应参考位置的阈值频率f_ref进行比较，由此确定换相点。

图4-7所示为频率调制法的变换器电路，输入为受检相绕组的电感L（θ），输出为对电感值敏感的振荡器信号频率f₀，且有

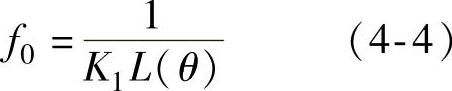
式中，K₁为由电路参数所决定的常数。

再经F/V变换，得

U₁=K₂f₀ （4-5）

由式（4-4）、式（4-5）得

式中，K为由K₁、K₂决定的常数，K=K₁/K₂。

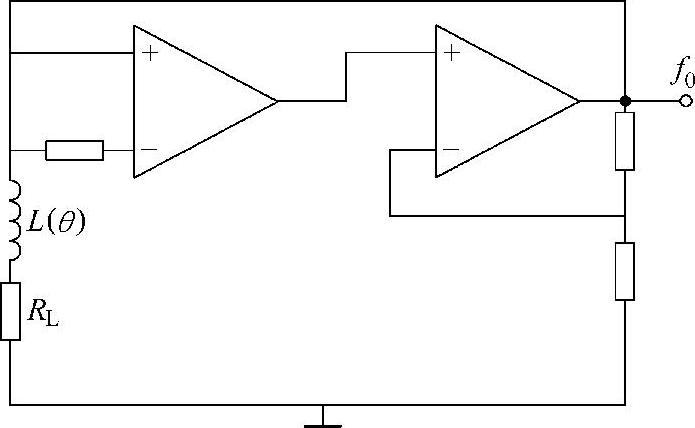
图4-7 频率调制变换器

式（4-6）表明，L（θ）与U₁成反比，因此通过U₁与所设阈值的比较，可获得转子位置信息。

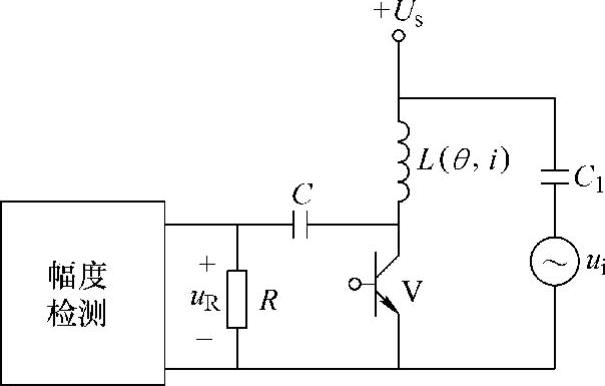
图4-8 利用相电感谐振检测转子 位置的电路（一相）

图4-8所示为利用受检相绕组电感谐振检测转子位置的电路^[100]。图中，当主开关器件V关断，即受检相处于非励磁状态时，将一频率固定为f₁的高频信号源u_i（C₁为耦合电容）接至由相电感L和RC网络组成的串联谐振电路，则电阻R两端的电压为

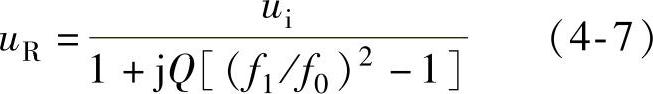
式中，f₀=1/（2πLC）；Q=1/（2πf₁RC）。

选择高频激励信号的频率f₁略大于最大谐振频率f_0max（对应于最小相电感L_min），显然对应于L_min处，u_R的幅值最大。

3.基于高频检测电压脉冲

即利用功率变换器直接给受检相施加宽度恒为Δt的高频检测电压脉冲，则受检相的脉冲响应电流幅值Δi与其相电感L（θ）成反比，根据式（4-2）可测得不饱和电感L（θ），进而可解算出转子位置。该方法无需外加激励信号源及辅助电路，便于实现，受到广泛重视。

本书以样机2[三相（6/4极）SR电动机]为例讨论基于高频检测电压脉冲间接测量转子位置的实现方法。样机2的不饱和电感分布曲线参数为：L_max=0.1825H，L_min=0.0108H，θ₂=14°，θ₃=44°，θ_a=45°，θ₄=46°，θ₅=76°。由此画出以A相定子凸极与转子凹槽中心重合为参考零位的三相不饱和电感分布曲线，如图4-9所示。

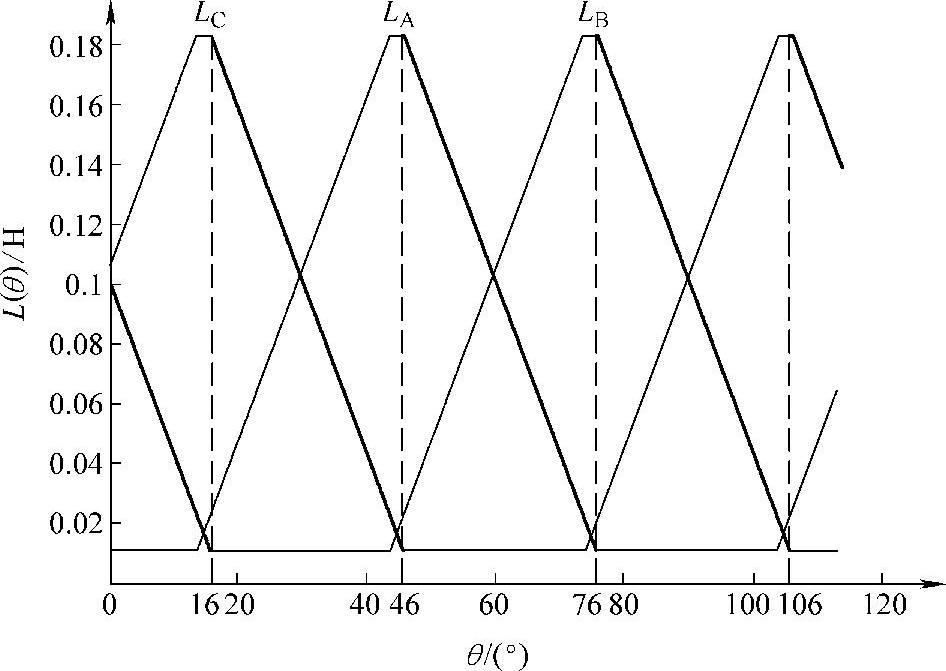
图4-9 样机2的三相不饱和电感分布曲线

SR电动机若为电动运行，应选择不饱和相电感的线性下降区[θ₄，θ₅]施加高频检测电压脉冲。因此，当转子处于[46°，76°）区间时，A相为受检相，由式（4-2）可计算出每一次激励脉冲作用后对应的相电感L（θ），然后根据式（4-8）估算转子瞬时位置，即

式中，K为相电感下降的斜率，有

当转子处于[16°，46°）区间时，C相为受检相，在应用式（4-2）、式（4-8）计算的基础上应加上60°，从而将估算的转子瞬时位置归算至以A相定子凸极与转子凹槽中心重合为零位的参考坐标系中，即

当转子处于[0°，16°）或[76°，90°]区间时，B相为受检相，在应用式（4-2）、式（4-8）计算的基础上应加上30°，以将测量B相电感获得的位置估算值归算至参考坐标系中，即

高频检测电压脉冲的频率和占空比是影响检测准确度的重要参数。当SR电动机转速一定时，激励脉冲频率若较低，则转子位置估算的分辨率低，检测准确度不高；但若激励脉冲频率过高，会出现相邻两次脉冲激励电流叠加的现象，导致检测失败。激励脉冲频率一般为（3～15）kHz^[100]。激励脉冲的占空比大，有利于提高检测准确度，但增加了检测功率损耗和制动转矩，一般可选为1∶3～1∶6^[104]。

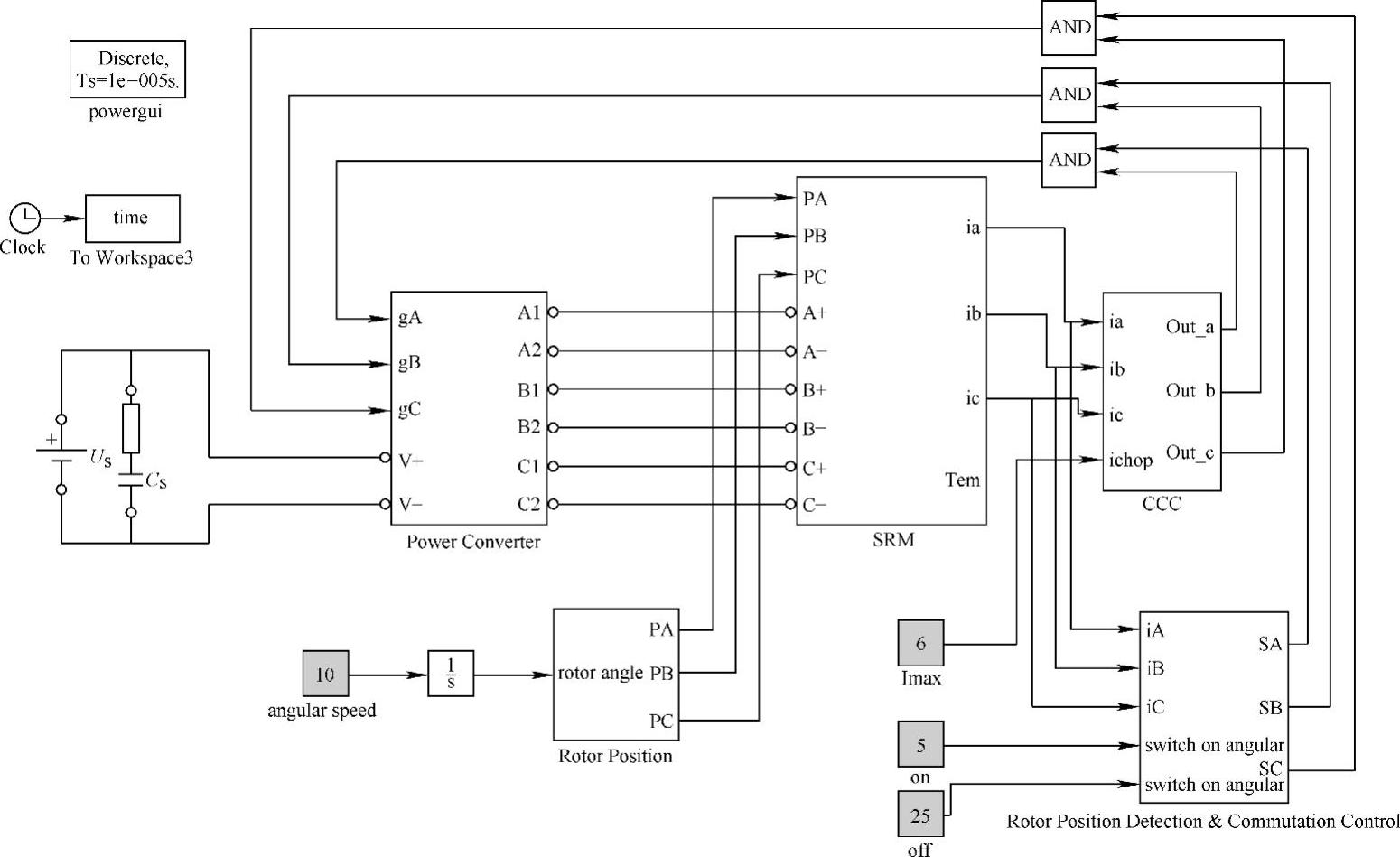
图4-10 样机2采用高频脉冲激励法间接测量转子位置的仿真模型

图4-10所示为以CCC方式运行在固定转速下的样机2采用高频脉冲激励法间接测量转子位置的仿真模型，其中，转子位置估算和换相逻辑控制（Rotor Position Detection&Commutation Control）模块的仿真模型如图4-11所示。图4-11中，SA、SB、SC分别为A、B、C相绕组的励磁控制信号或测试脉冲控制信号，其根据估算的转子位置信息由控制逻辑产生。位置估算采用MATLAB Function（功能）模块根据式（4-2）、式（4-8）、式（4-10）、式（4-11）编程实现，其输入为一次高频脉冲结束信号、三相电流信号及其是励磁电流还是测试脉冲响应电流的标志信号，输出则为归算至参考坐标系中的转子瞬时位置θ。Position Detection（位置检测）模块（其仿真模型与图2-45基本相同）则将估算得到的θ值映射为与转子相对A、B、C三相绕组的位置角PA、PB、PC。

当样机2在CCC方式下运行的角速度ω_r=10rad/s，初始位置θ₀=45°（即A相定子凸极与转子凸极中心重合）时，采用占空比为0.4、频率1kHz的激励脉冲进行转子位置估算的仿真结果如图4-12所示。

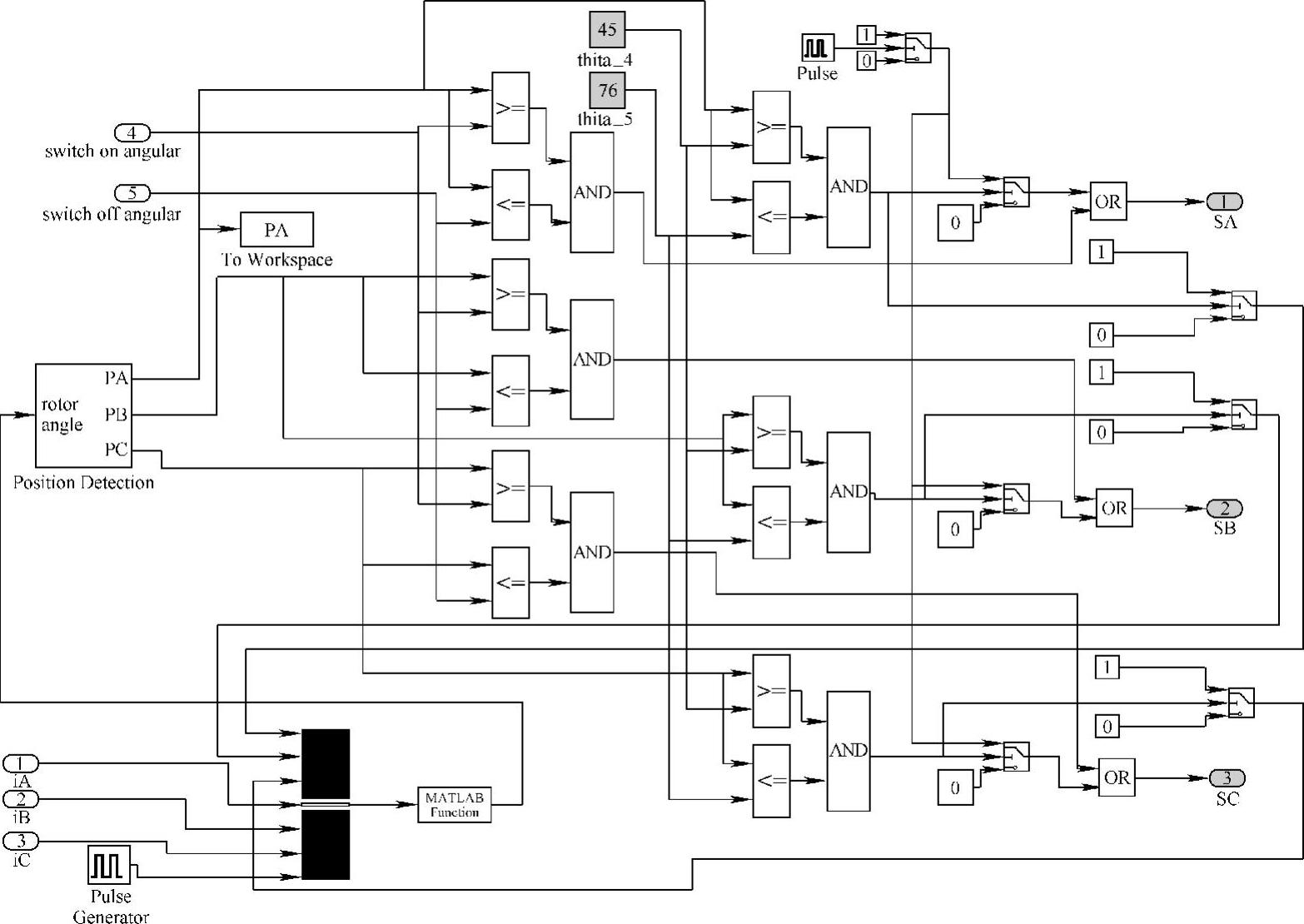
图4-11 转子位置估算和换相逻辑控制模块的仿真模型

在图4-10所示的仿真模型的基础上建立了CCC方式下样机2基于高频脉冲激励法间接检测转子位置的无位置传感器闭环调速系统仿真模型，图4-13所示为给定角速度为ω_r^∗=10rad/s、初始位置θ₀=45°、负载转矩0.1N·m、θ_on=-5°、θ_off=40°时起动性能仿真结果。

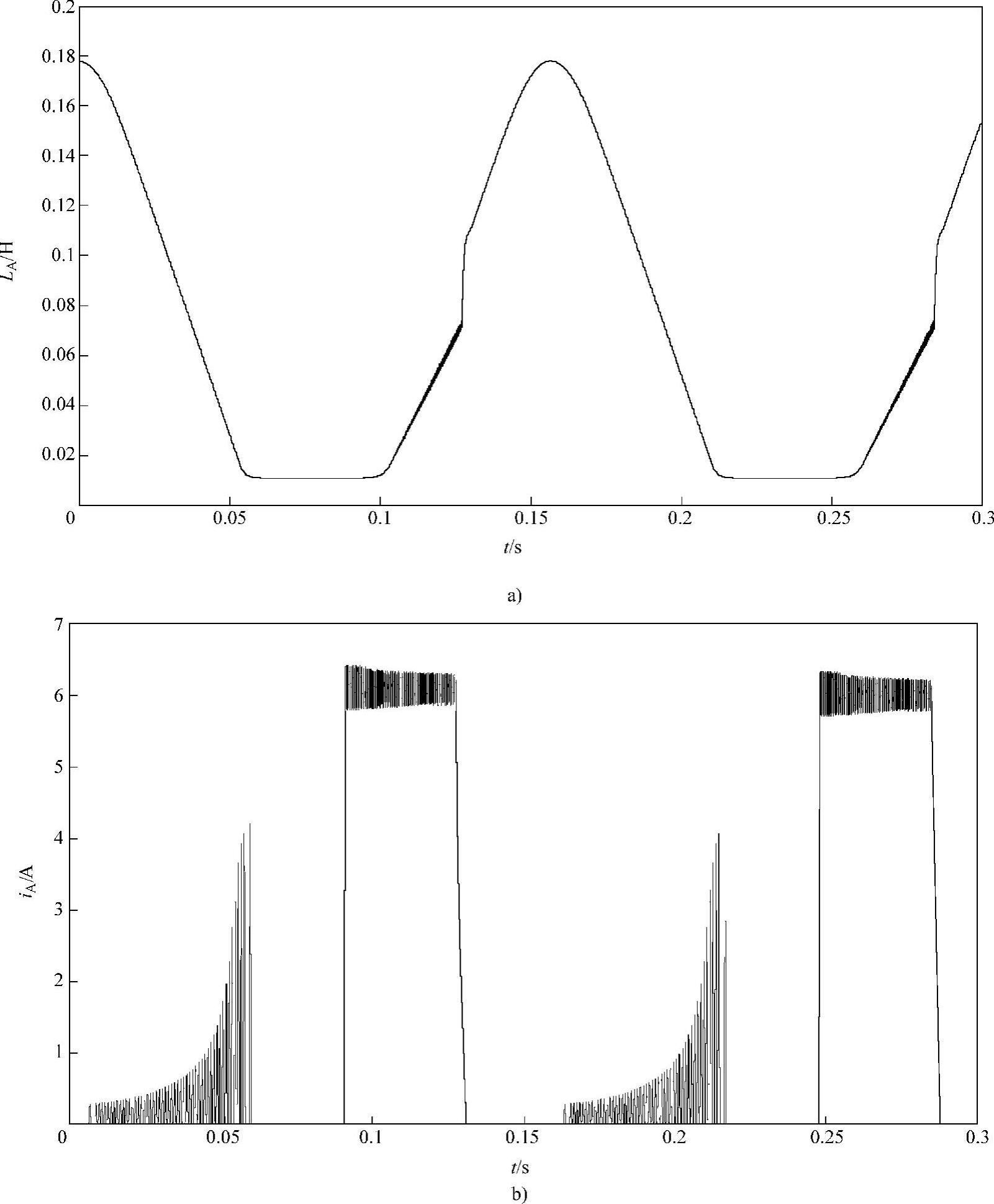
图4-12 高频脉冲激励法间接测量转子位置仿真结果（ω_r=10rad/s）

a）A相电感 b）A相励磁电流和测试电流

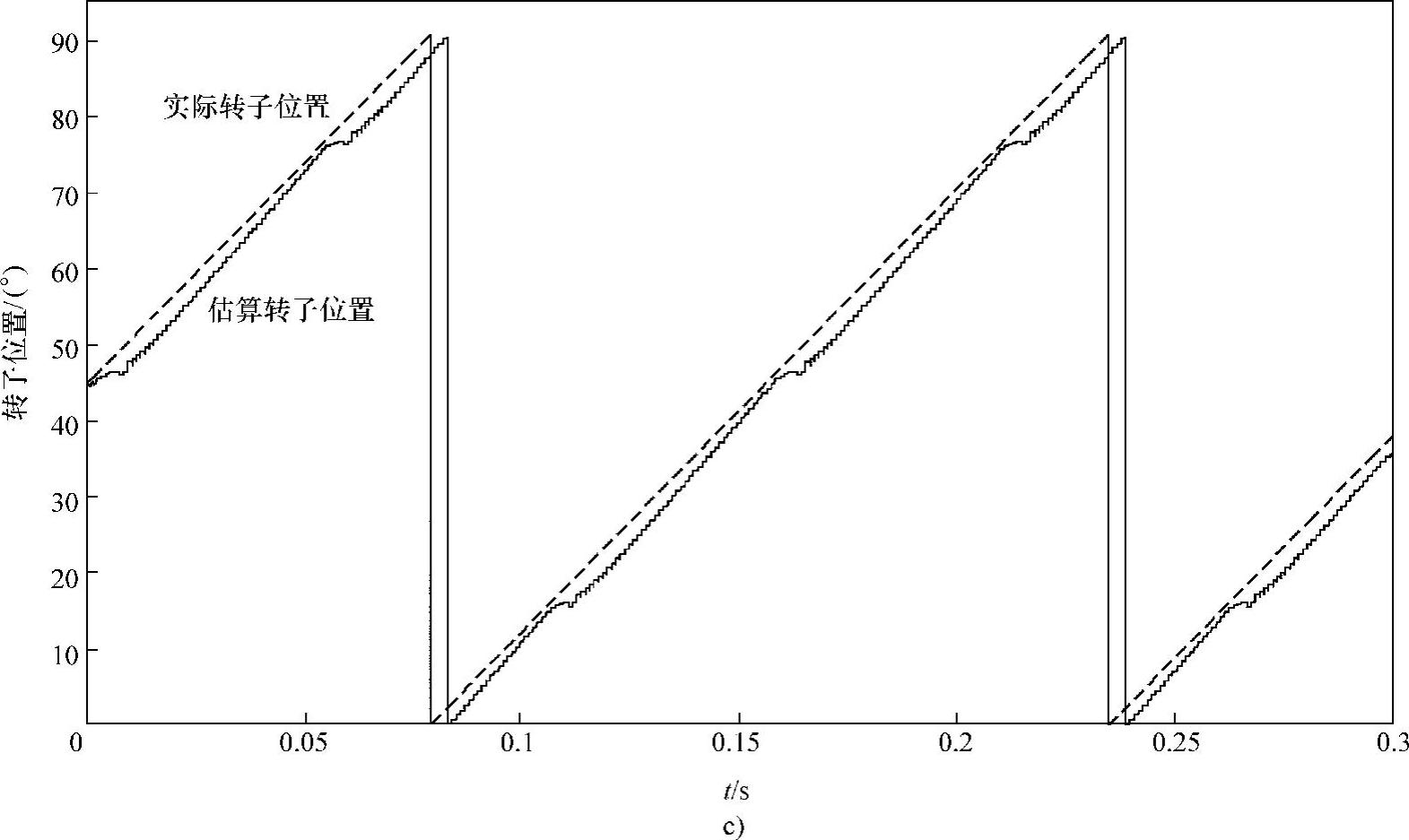
图4-12 高频脉冲激励法间接测量转子位置仿真结果（ω_r=10rad/s）（续）

c）实际转子位置与估算的转子位置

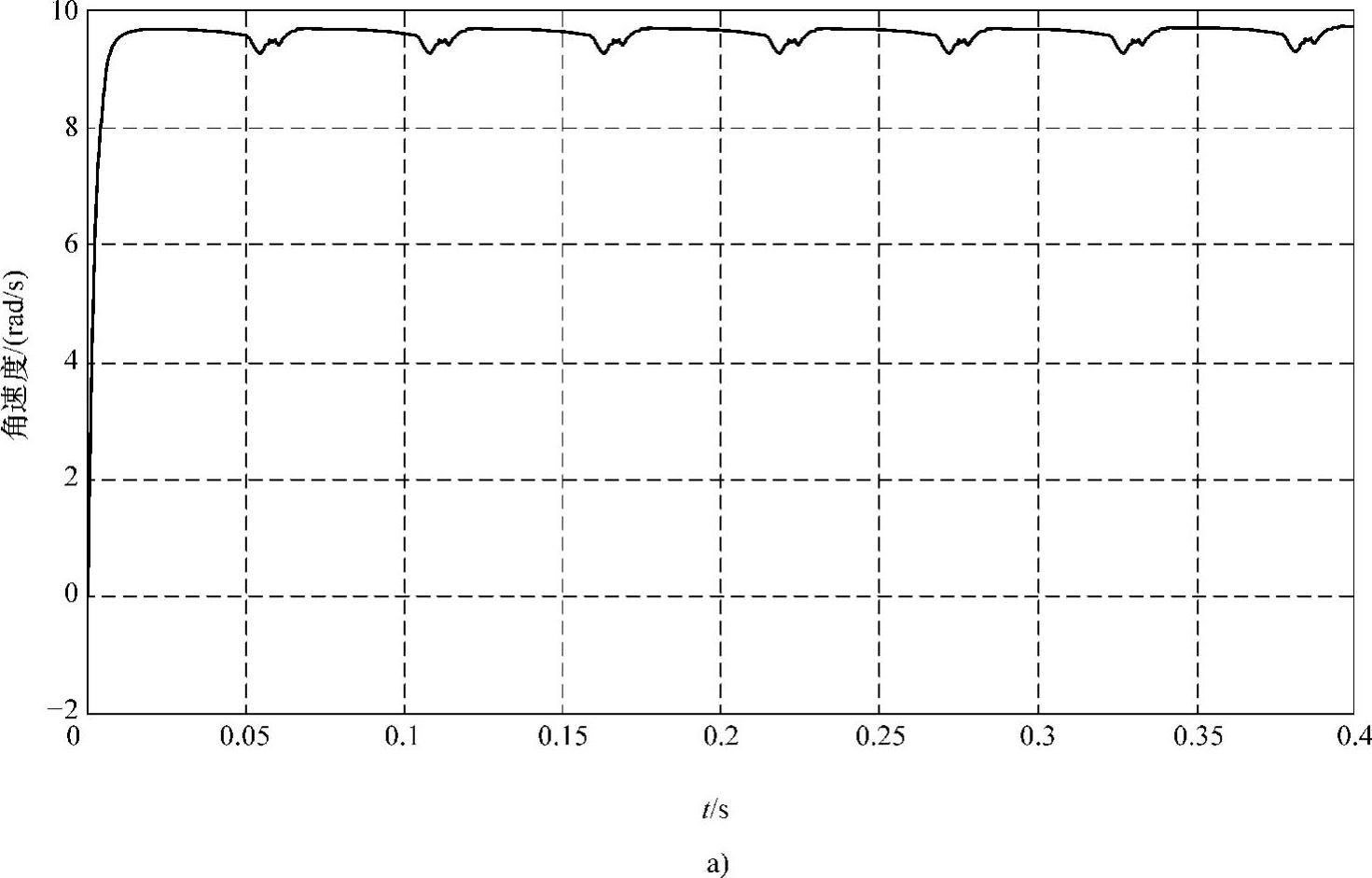
图4-13 无位置传感器闭环SRD起动性能仿真(www.xing528.com)

a）角速度

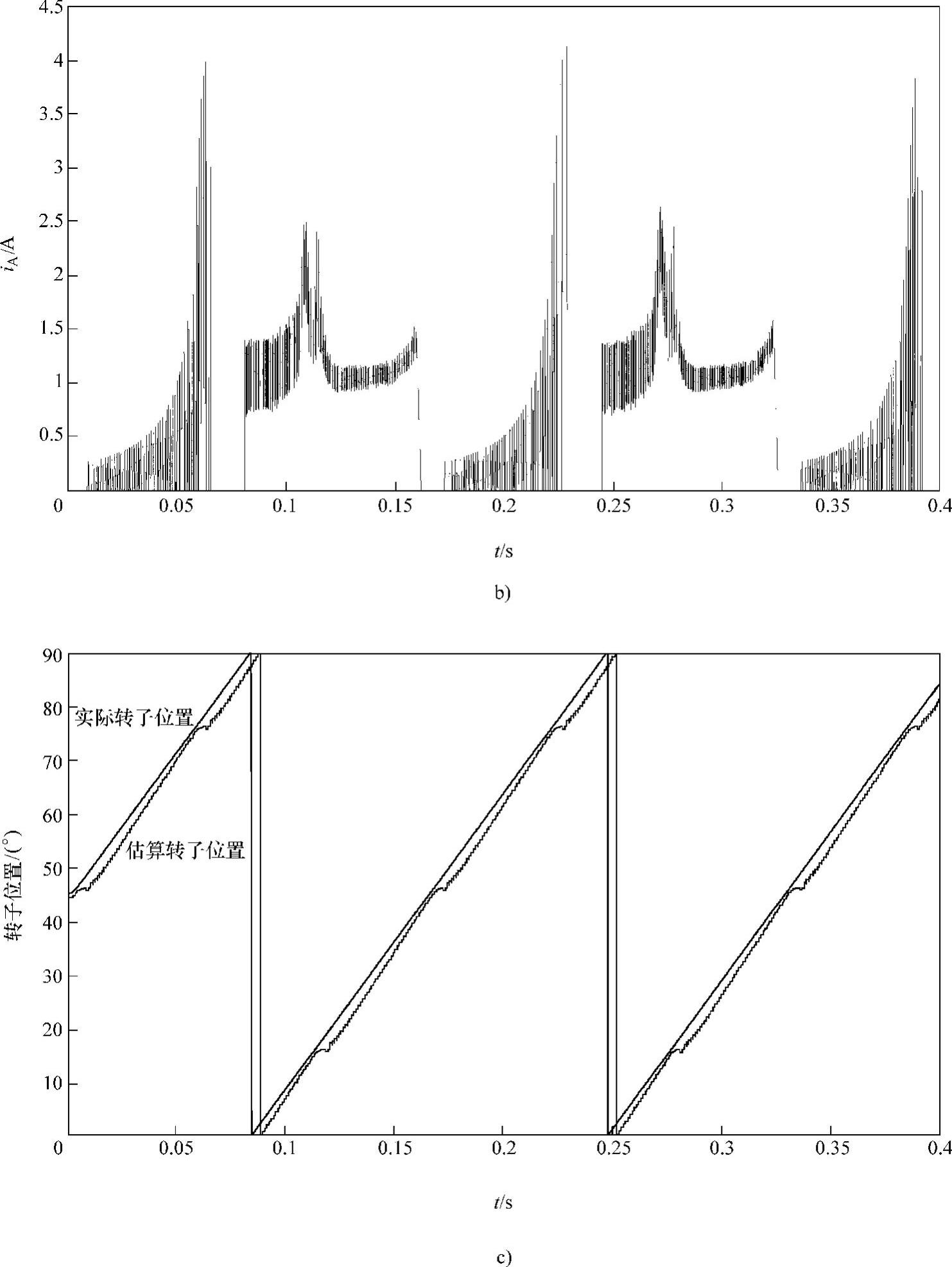
图4-13 无位置传感器闭环SRD起动性能仿真（续）

b）A相励磁电流和测试电流 c）实际转子位置与估算的转子位置

上述任一瞬时仅有一相作为受检相施加高频检测电压脉冲的转子位置估算方法具有判别逻辑简单、易于实现的优点，但在受检相切换时检测误差较大，且易受电压波动和负载变化的影响。为提高检测准确度和可靠性，参考文献[196]提出了一种对两非工作相施加高频检测电压脉冲，比较其响应电流变化以确定换相点的方法。

4.2.2.2 适用于较高速度范围内运行的转子位置间接检测方法

这类方法的共同特点是直接检测相绕组的励磁电流进行转子位置估算，无需附加的测试信号生成及切换电路。其具体实现途径有如下几种：

1.磁链/电流法

该方法在忽略相间互感的前提下，基于SR电动机相绕组磁链与相电流、转子位置的非线性关系，利用实测的励磁相电流和相电压，计算相绕组磁链，并与相电流一起通过插值查预先存储的电动机磁链-电流-位置角三维数据表[105]或智能逼近等方法进行转子位置估计或换相逻辑判别。

由SR电动机的相电压平衡方程式（2-2），k相绕组在时刻t的磁链应按下式计算：

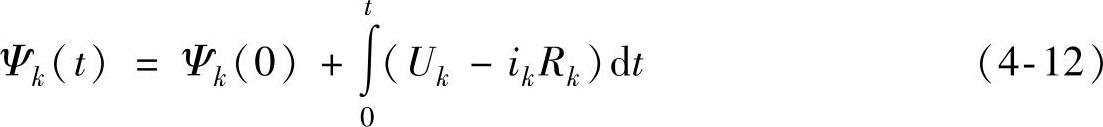
式中，R_k为k相绕组电阻的估计值。

相绕组电阻与温度有关，难以准确估计，这是影响磁链计算精度的重要因素。对于APC方式运行，因在相绕组励磁阶段，相电压极性始终为正，故应用式（4-12）可获得较高精度的相磁链计算值，而且当Uk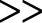i_kR_k，即使在式（4-12）中忽略i_kR_k，亦有足够的磁链计算精度。但若采用CCC方式，在相绕组励磁阶段，相电压正负交替变化，正向相电压的伏秒积大都被反向相电压的伏秒积抵消，而相电阻压降i_kR_k的伏秒积是同一极性的，在相磁链计算中的作用十分显著，不可忽略。因此，该方法适用于APC方式下高速运行，不适合CCC方式下低速运行。

针对传统磁链/电流法需预先存储磁链-电流-位置角三维数据表，占用内存大、算法复杂、实时性差的局限，参考文献[106]在SR电动机单相轮流导通的条件下，将转子位置检测简化为换相位置判别，若根据式（4-12）估算的导通相绕组磁链值大于与当前电流对应的换相位置磁链，则关断该绕组，导通下一相。而与当前电流对应的换相位置磁链通过插值查最大电感位置处磁链-电流二维数据表，并将查得的磁链乘以小于1的系数获得，该“简化磁链法”只需预先存储最大电感位置处的磁链-电流二维数据表，占用内存小，算法简单、快速。参考文献[108]针对“简化磁链法”换相位置不易确定的缺点，将相电感曲线的交点作为特征位置，提出了一种基于特征位置磁链特性检测的改进型简化磁链位置估计方法。

磁链/电流法估计转子位置问题可等效为以相绕组磁链、电流为输入，转子位置角为输出的非线性逼近问题，因此非线性函数逼近能力强的模糊逻辑、神经网络等智能拟合算法^[118-121]为建立SR电动机转子位置预测模型提供了新途径。

2.电感解析模型法

若忽略相间互感，励磁相电感可用其自感模型描述，即^[112]

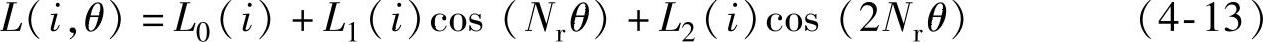
式中，N_r为转子极数；L₀、L₁、L₂由下式确定：

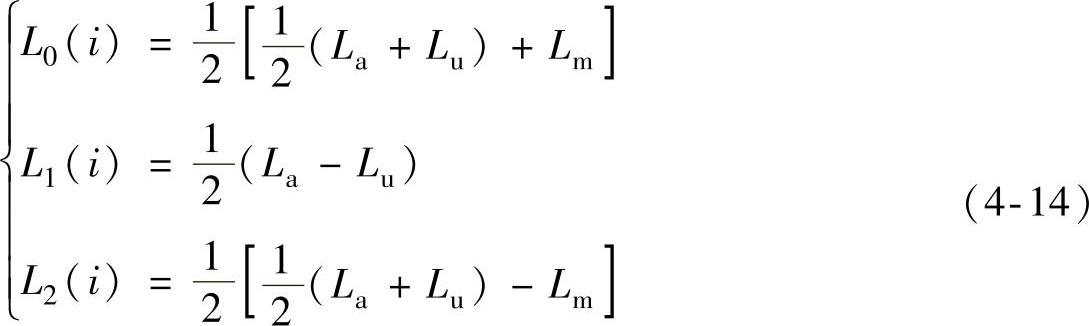
式中，L_a、L_u、Lm分别为定子凸极与转子凸极中心重合位置（设为横坐标原点，即θ=0）处电感、定子凸极与转子凹槽中心重合位置（θ=π/N_r）处电感、定转子凸极中心重合位置与定子凸极与转子凹槽中心重合位置间的中间位置[θ=π/（2N_r）]处电感。其中，L_u为与相电流i无关的常数；L_a、L_m均为相电流i的非线性函数，可采用多项式拟合，即

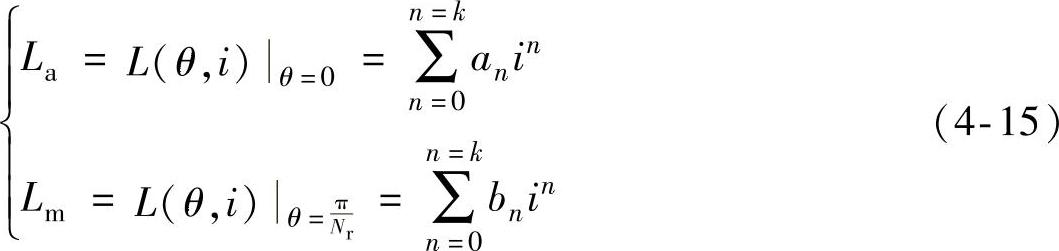
式中，n为拟合多项式的幂次，一般取n=5即可达到良好的拟合准确度^[112]。

式（4-13）所示的电感解析模型只需测量3个特殊位置处的相自感即可建立，在此基础上，通过测量励磁相绕组的电感和电流，即可估算出转子位置。

3.状态观测器法

参考文献[114]提出基于m相SR电动机线性模型，选择相绕组磁链、转子位置角θ、角速度ω_r为状态变量，以相电压为输入，相电流为输出，建立了其对应的状态空间表达式，即

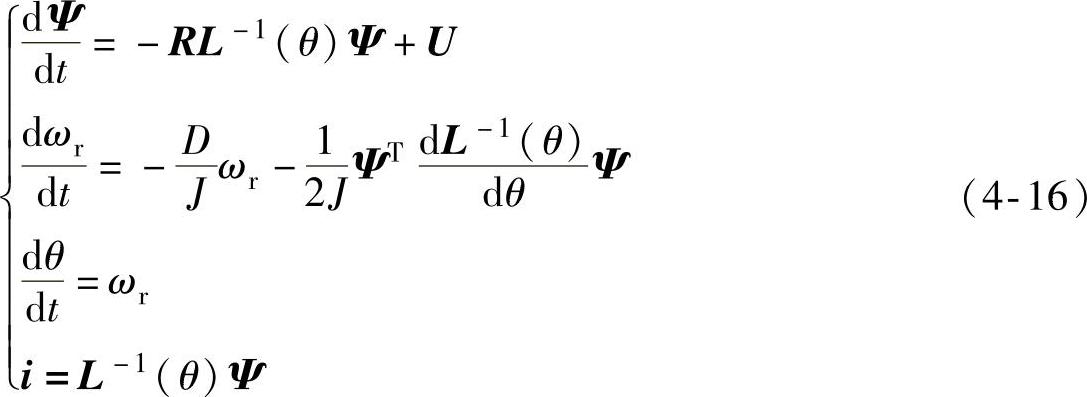
式中，U为相电压列矢量，U=[U₁，U₂，…，U_m]^T；i为相电流列矢量，i=[i₁，i2，…，i_m]^T；Ψ为相磁链列矢量，Ψ=[Ψ₁，Ψ₂，…，Ψ_m]^T；R为相绕组电阻矩阵，R=diag（R₁，R₂，…，R_m）；L^-1（θ）为相电感矩阵的逆矩阵，L^-1（θ）=diag（L₁（θ）-1，L₂（θ）-1，…，L_m（θ）-1）；D为粘性摩擦系数；Ψ^T为Ψ的转置矩阵；J为转动惯量。

引入输出偏差反馈的闭环观测器状态空间表达式为

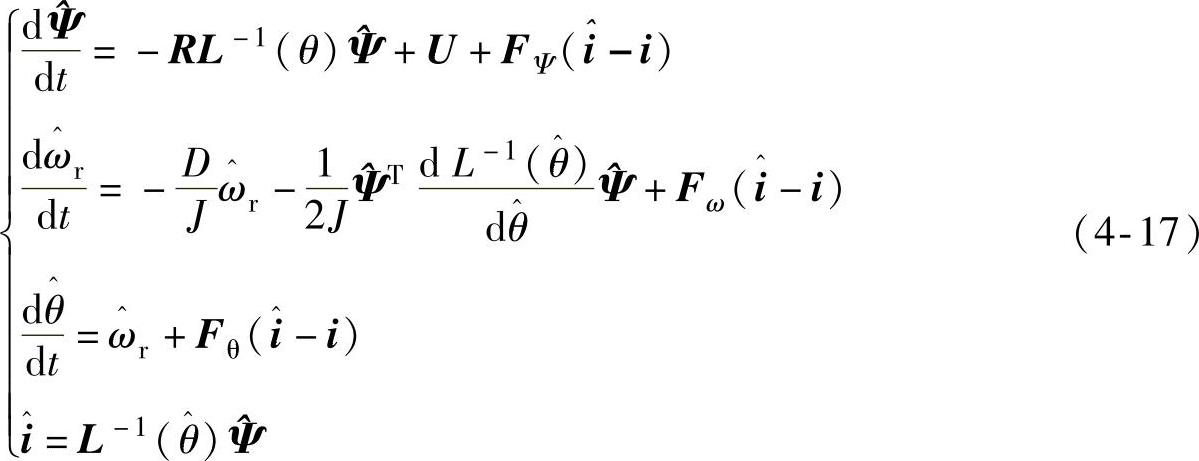
式中，变量符号上方加“∧”号表示对应状态变量的估计值。

与式（4-17）对应的状态观测器原理框图如图4-14所示。

图4-14中，FΨ为待设计的状态观测器增益矩阵，Fω、F_θ则为待设计的状态观察器的增益矢量，其决定了观测误差趋于零的收敛速率。参考文献[114]假设转子惯性为无穷大（即设J→∞），故在式（4-16）所示的模型中的转子动力学方程中，未计及负载转矩这一外部扰动项，忽略了因转速波动引起的非线性，采用线性系统状态观测器理论简化了观测器增益设计，但降低了观测器动态运行的快速响应性。事实上，负载转矩是存在的，而且由于速度波动，即使稳态运行亦难准确获悉。为此，参考文献[115]在转子动力学方程中计及了负载转矩的作用，且将负载转矩亦作为状态变量之一，建立了SRD增广非线性状态方程，并得到其一次近似线性化模型，设计了龙伯格降维观测器，根据检测的相电压、相电流对速度、位置角和负载转矩进行估算。

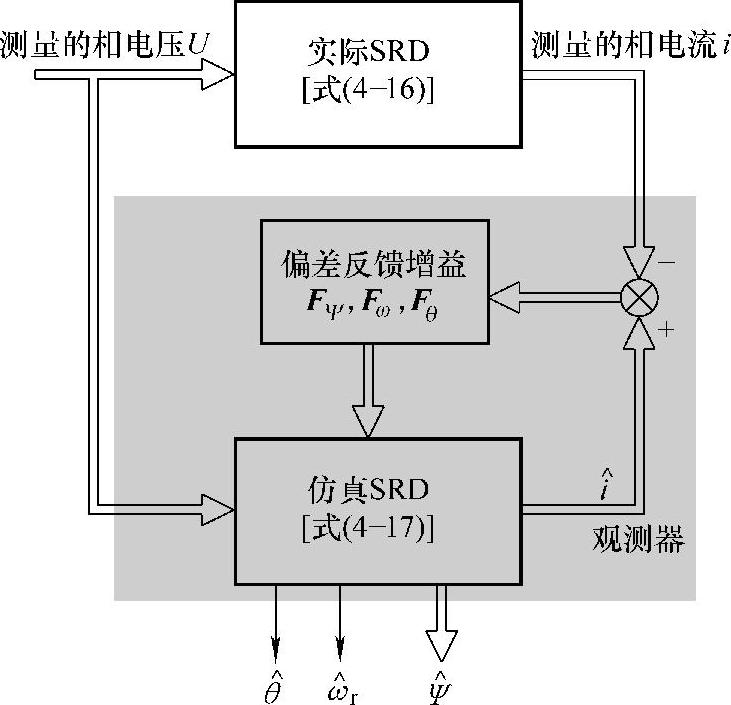
图4-14 状态观测器原理框图

4.相电流梯度法

如图2-6所示，θ₂定义为转子极前沿与定子极后沿相遇的位置角。若以0-表示转子刚到达θ₂位置的前一时刻，0+表示转子刚转过θ₂位置的后一时刻，忽略相绕组电阻的压降，则由式（2-22）得励磁相绕组在0-、0+时刻的电压方程式为

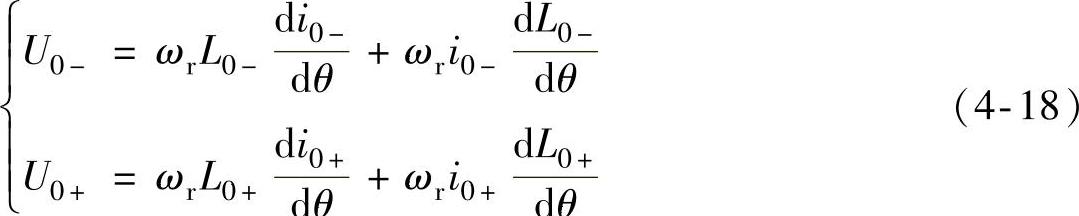
式中，L_0-=L₀₊≈L_min，dL_0-/dθ≈0。则式（4-18）可简化为

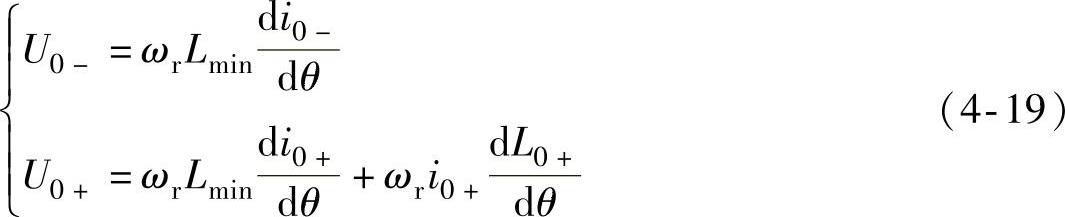
若θ_on＜θ₂，则U_0-=U₀₊=U_s，由式（4-19），得

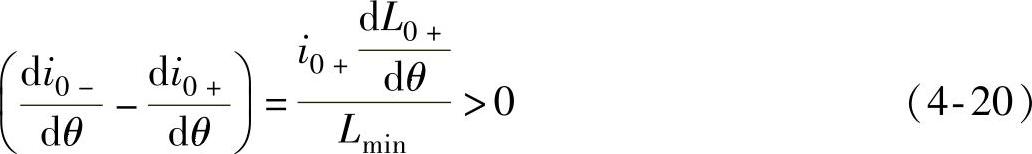
式（4-20）表明，在位置角θ₂处相电流的梯度将下降。参考文献[110]提出了基于SR电动机的这一特征，以式（4-20）为判据确定转子是否到达θ₂位置的“相电流梯度法”。比较前后相邻两相检测到θ₂位置的时间差，可估算SR电动机的角速度为

式中，m为SR电动机的相数；N_r为转子极数；t_0（k-1）、t_0（k）分别为前、后相邻两相检测到θ₂位置的时间。

励磁相绕组在时刻t₀（k）检测到θ₂位置后，基于估算的角速度，可估算任一时刻t的转子位置作为换相的依据，即

θ（t）=θ₂+ω（t-t_0（k）） （4-22）

上述电流梯度法的优点是无需相电感的先验知识，亦不需要存储磁化曲线数据和额外增加硬件电路，实现简单，适用于中、高速电压PWM和APC方式运行，不会降低SRD的性能。但低速运行和重载运行时，限流保护动作亦会导致电流梯度下降，这时若采用电流梯度法检测θ₂位置会造成误判，因此它不适用于低速、重载运行；另外，该方法对于负载、转速快速变化的场合亦不适用。

对于电压PWM方式运行，应将相电流经低通滤波器，以滤除高频斩波信号，得到相电流检测信号。图4-15所示为样机2采用电压PWM方式（θ_on=0°，θ_off=30°，斩波频率为5kHz，占空比为0.5）开环运行在1000r/min时，应用电流梯度法间接检测转子位置的仿真结果。低通滤波器的参数和电流信号的采样周期对位置检测准确度影响较大，图4-15所示的仿真结果中，采用了惯性时间常数为0.000001s的一阶低通滤波器，相电流检测信号的采样周期为0.3ms。

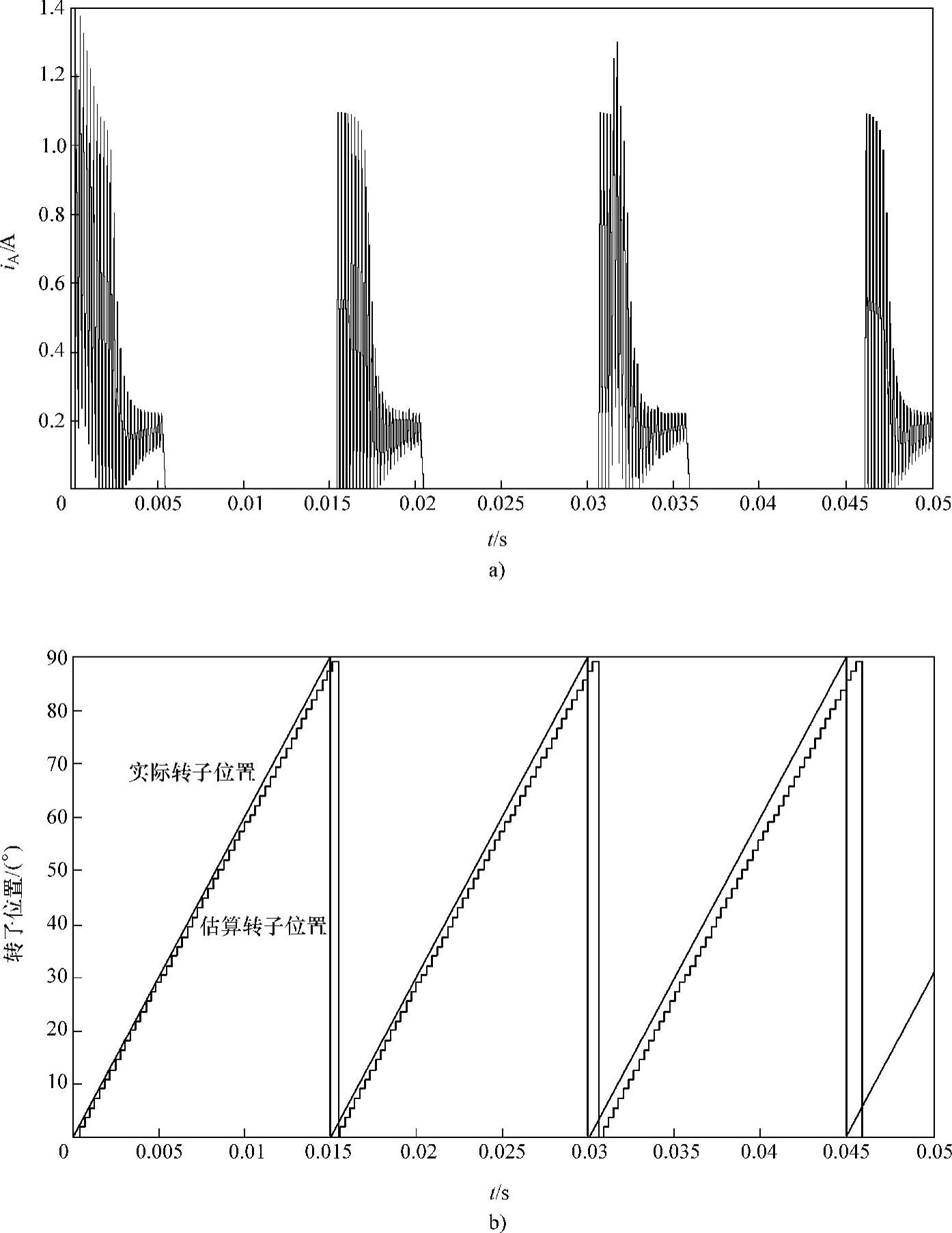
图4-15 相电流梯度法间接测量转子位置仿真结果（电压PWM方式运行）

a）A相电流 b）实际转子位置与估算的转子位置

对于APC方式运行，可省去低通滤波器，直接将相电流作为检测信号。图4-16所示为样机2采用APC方式（θ_on=0°，θ_off=30°）开环运行在1200r/min时，应用电流梯度法间接检测转子位置的仿真结果，相电流的采样周期为0.2ms。

应该指出，当θ=θ_off、相绕组关断时，亦会导致相电流梯度下降^[126]，在应用电流梯度法检测转子位置时，需要区别θ=θ₂和θ=θ_off这两个不同的位置，以免误判。

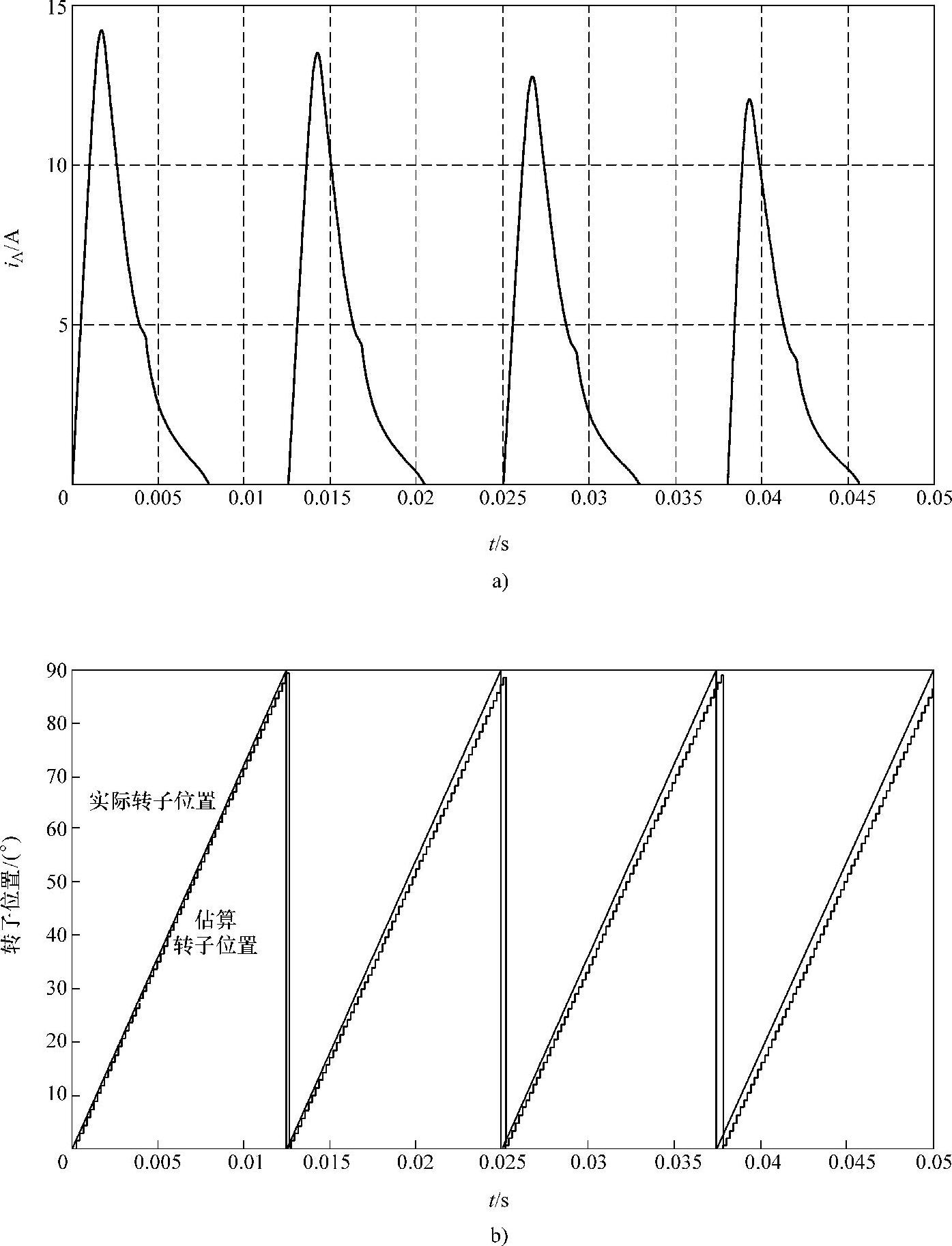
图4-16 相电流梯度法间接测量转子位置仿真结果（APC方式运行）

a）A相电流 b）实际转子位置与估算的转子位置