以电流定额为目标的系统优化设计

基于式（2-9）所描述的SR电动机线性模型，不同结构参数的SR电动机将对应不同形状的分段线性电感-角度特性L（θ）。而对每一条电感曲线，均可分析得出与不同速度对应的不同θ_on、θ_off组合的一系列电流波形，这些电流波形均可解析，因此可计算出对应的有效值、峰值电流，从而在一定电感曲线L（θ）下，可通过θ_on、θ_off的选择满足SRD恒功率（APC方式）、恒转矩（CCC方式）运行的需要，并使主开关器件的电流定额要求最小。应用计算机对各种不同的电感曲线进行反复迭代计算，即能确定使系统成本最小所希望的SR电动机相电感曲线和相电流波形。应用上述优化设计方法最终确定的最小电流定额，只要加上考虑到饱和因素的修正量即可作为主开关器件选型的依据。

1.满足输出恒功率特性的有效值电流定额

由式（1-10），基于线性模型的SR电动机一相绕组在其电感上升区的瞬时转矩为

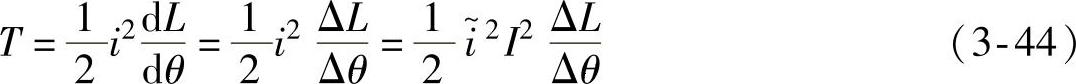
将电流基值I=U_sΔθ/（ω_rΔL）代入式（3-44），得

则SR电动机每相绕组产生的平均转矩T_av、平均功率P分别为

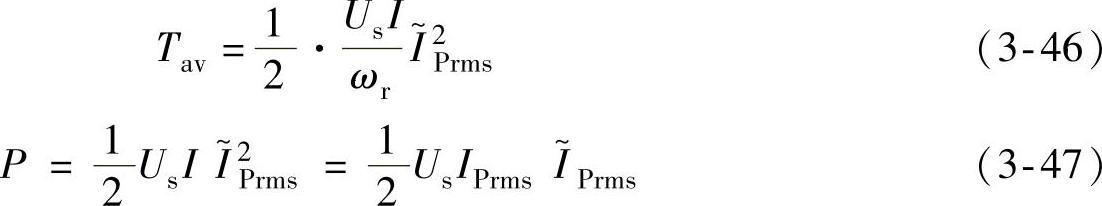
在一定的电感分布曲线下，只要给出一组θ_on、θ_off，根据式（3-41）～式（3-43）即可求出对应的用相对值表示的有效值电流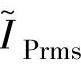、、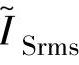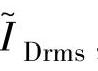，若P和Us给定，则根据式（3-47）即可求出电流基值I，进而可求出相绕组、主开关器件、续流二极管电流有效值的实际值I_Prms、I_Srms、I_Drms。可输入不同的θ_on、θ_off组合，让计算机重复上述计算过程。

由2.5节的分析知，在基速ω_b至第二临界角速度ω_sc的速度范围内，SR电动机运行在APC方式下，可输出恒功率特性。将电流基值I=U_sΔθ/（ω_rΔL）代入式（3-47），得

(www.xing528.com)

式（3-48）表明，若要在ω_b至ω_sc的角速度范围内使SR电动机均输出额定功率，则对应不同的转速应选择不同的相电流脉冲，第二临界角速度ω_sc所对应的与基速ω_b对应的应当满足如下恒功率约束条件，即

因为基值电流I随角速度ω_r增大成反比减小，故要在ω_b至ω_sc的角速度范围内保持恒功率输出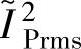，必须随角速度ω_r的增大成正比增大[参见式（3-47）]，则实际的相电流有效值I_Prms正比于ω_r^-1/2，即I_Prms²随ω_r增大成反比减小。

综上所述，若以输出额定功率作为约束条件，器件的电流定额将取决于基速产生额定转矩所需的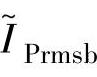，其与所选择的θ_on、θ_off有关。而式（3-49）即为根据某一θ_on、θ_off的组合，算出的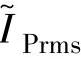是否为基速产生额定转矩所需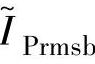的判据。所以，在一定的电感分布曲线下，可选择θ_on、θ_off使其满足式（3-49）所示的恒功率约束条件，且在输出额定功率下使主开关器件的有效值电流定额最小。对各种可供选择的电感分布曲线重复上述优化分析过程，最终可确定使主开关器件有效值电流定额全局最小的期望电感分布曲线和最优θ_on、θ_off组合。

2.满足输出恒转矩特性的峰值电流定额

上述分析表明，主开关器件的有效值电流定额是以基速运行输出额定功率为条件确定的。由2.5节的分析知，在基速以下，SR电动机运行在CCC方式下，可输出恒转矩特性。

设CCC方式下的斩波相电流近似为矩形波，幅值为I_MC，θ_off-θ_on=2π/（N_rm）（其中，m为SR电动机相数，N_r为转子凸极数），且设相电流只在电感上升区流动，根据式（3-34）得其有效值为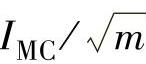。因为CCC方式下输出转矩即为基速转矩，所以斩波电流有效值应与基速时电流有效值相等，即

如图2-32所示，式（3-50）表示CCC方式斩波区电流平均值与基速相电流有效值的关系，显然，峰值电流要略大于I_MC，这取决于ΔI（=i_H-i_L）的大小。