SR电动机的能量比率与广义功率因数解析

由第2章分析可知，SR电动机相绕组在导电期间从外电源吸收的电能并未完全转换为机械功率输出，因为在相电流续流期间，相绕组储存的部分磁能将回馈给电源，这就导致这部分能量在SR电动机和功率变换器之间往返交换。为了度量SR电动机在每一转子角周期中单位输入电能转换为机械能的大小，参考文献[1]定义SR电动机的“能量比率（ER）”为

能量比率ER可视为传统交流电动机中功率因数概念在SRD中的推广，其大小是考察SR电动机运行性能与成本的一个指标。

第2章中已指出，SR电动机一相绕组在一个转子角周期内的机电能量转换过程可由Ψ-i-θ磁化曲线族和Ψ-i轨迹图来说明。图3-7所示为样机1非线性磁化曲线族以及相电流为理想斩波控制（参见图2-15）时的Ψ-i轨迹，设在最小电感位置θ_u处通电，在最大电感位置θ_a处断电。

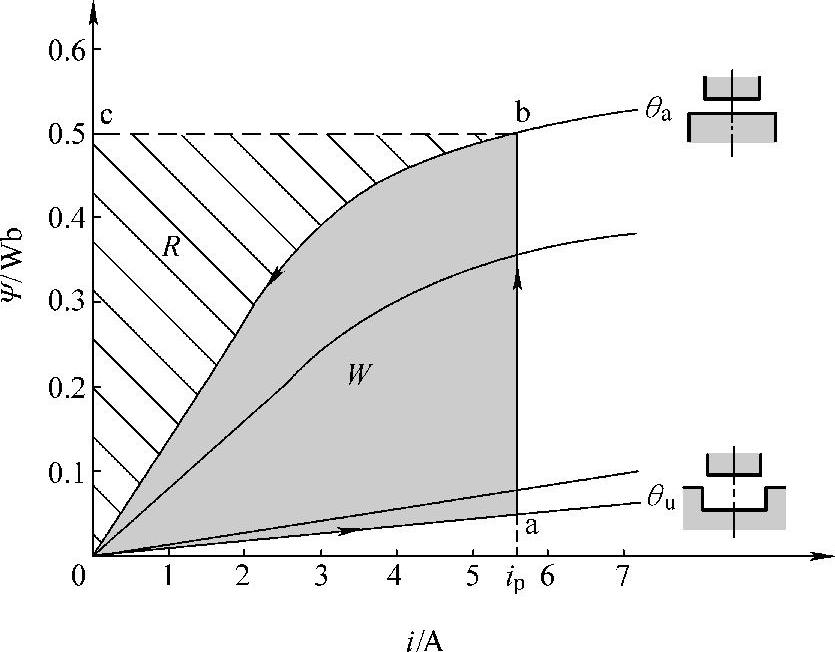
图3-7 SR电动机的典型Ψ-i-θ曲线及理想的Ψ-i轨迹

由机电能量转换原理知，图3-7所示面积0abc0表示SR电动机由θ_u转到换相点θ_a从电源吸收的能量（W+R）；面积0bc0则表示在换相点θ_a处相绕组中尚储存的磁能（图中打斜线的区域R），若不计变换器损耗，这部分储能将在换相后返还给电源；面积0ab0表示则表示该相在一个转子角周期内转换为机械功的能量（W）。对应于图3-7描述的过程，式（3-6）即为

若SR电动机不饱和，磁化曲线是一族直线，如图3-8所示。由图3-8可得

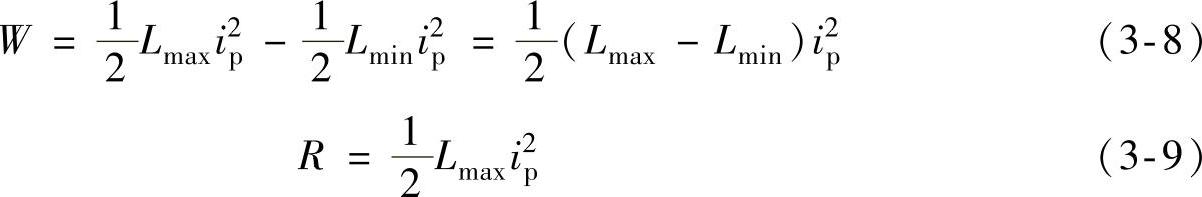
将式（3-8）、式（3-9）代入式（3-7），可得不饱和SR电动机的能量比率ER为

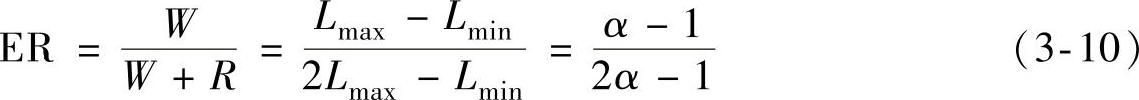
式中，α=L_max/L_min。

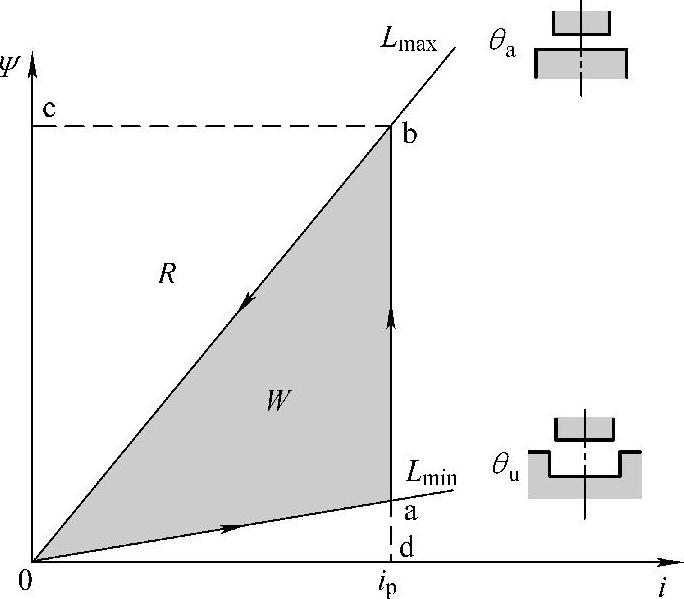
图3-8 不饱和SR电动机的Ψ-i-θ曲线及理想的Ψ-i轨迹

若α=6，由式（3-10），则ER=0.455。显然，随着最大与最小电感比α的增大，能量比率亦随之增大，但对于不饱和SR电动机，其能量比率的最大极限值为0.5。

对饱和的SR电动机，若采用图2-13b所示的准线性模型，即用分两段线性的Ψ-i-θ磁化曲线族近似实际的非线性磁化曲线族，则图3-7近似为图3-9。

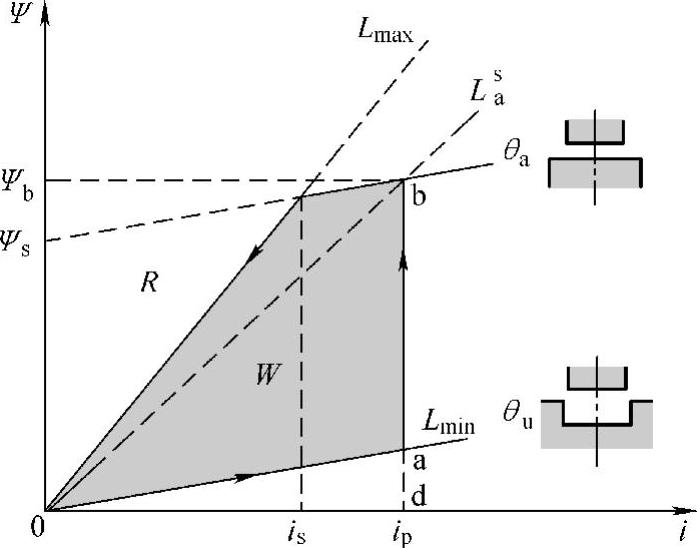
图3-9 饱和SR电动机的近似Ψ-i-θ曲线及理想的Ψ-i轨迹

用L_a^s表示定、转子凸极轴线重合位置θ_a处的饱和电感，定义饱和因数σ为

由图3-9有

L_maxi_s=L_mini_s+Ψ_s （3-12）

整理式（3-12），得(www.xing528.com)

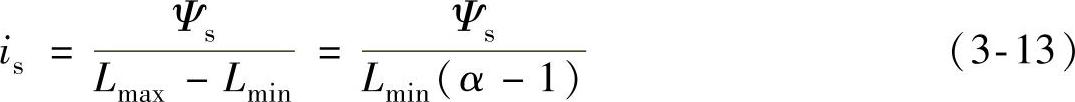
由式（2-16）知，绕组通电期间磁链近似以U_s/ω_r的速率线性增长，则有

式中，θ_ab为从a点至b点转子转过的角度。

为进一步简化分析，不妨设θ_ab≈β_s，其中β_s为定子极弧角，这相当于近似认为相电感上升区间的角度范围为β_s（=θ₃-θ₂），由此得

而b点处的磁链为

则

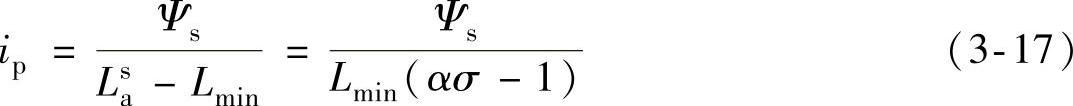
由式（3-13）和式（3-17）得

式中，c=（α-1）/（ασ-1）。 （3-19）

由图3-9有

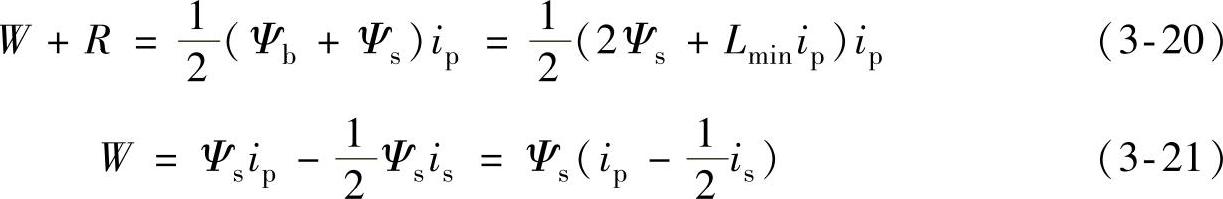
将式（3-15）、式（3-17）、式（3-18）分别代入式（3-20）、式（3-21），得

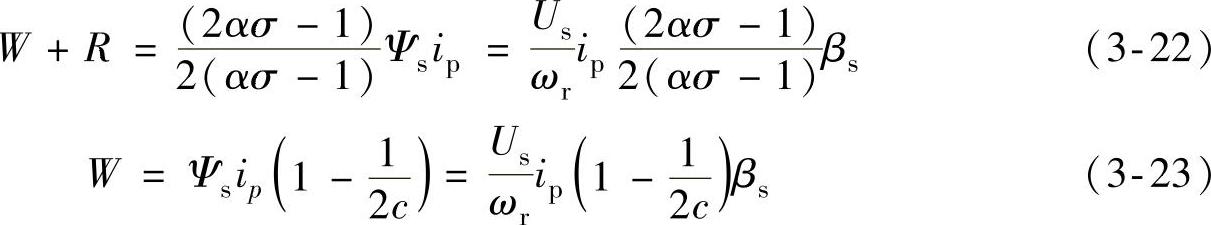
将式（3-22）和式（3-23）代入式（3-7），即得SR电动机饱和条件下的能量比率ER为

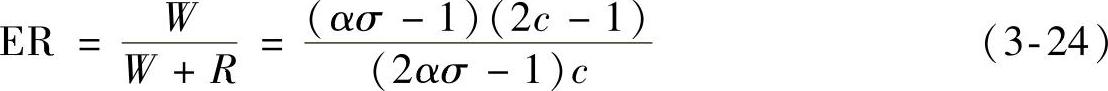
只要将与不饱和条件对应的σ=L_a^s/L_max=L_max/L_max=1、c=（α-1）/（ασ-1）=1代入式（3-24），即可推得式（3-10）。

由图3-9可见，饱和条件下的ER值将超过0.5，一般可做到0.6以上。例如，若饱和因数σ=0.4，当α=6时，则c=3.75，代入式（3-24），算得其ER=0.633。

应该指出，上述关于ER值的分析是基于假设相电流为按理想斩波的平顶波电流，并且相绕组在最小电感位置处通电，在最大电感位置处断电，这与SRD实际运行的情况是有较大出入的。例如，实际上，SRD在低速CCC方式下运行时，其相电流波形如图2-32所示，并非平顶波；而且换相通常是提前的，即在θ_a点之前关断相绕组，这样在θ_a处相电流基本已衰减至零。

由2.7.2节知，CCC方式在斩波段有ERCC、NERCC两种续流方式。对ERCC方式而言，因在斩波续流期间，idΨ＜0，绕组有部分储能回馈给电源，故降低了能量比率ER值；对NERCC而言，在斩波续流期间，idΨ=0，即SR电动机既不从电源吸收电能，也不向电源回馈磁能，相绕组储能全部用于输出机械能，无附加的能量回流，与ERCC方式相比，提高了ER值。此外，适当提前换相，亦可提高ER值，这是因为若在θ_a点之前换相，绕组储存的能量还有部分可转变成机械能输出。实际上，只要通过优化θ_on、θ_off，即使在低速斩波时，不饱和SR电动机的ER值仍可高于式（3-10）的最大极限值（0.5）^[23]。