基于非线性模型的SR电动机稳态运行仿真优化

由式（2-2），不失一般性，将任一相的电压平衡方程改写为

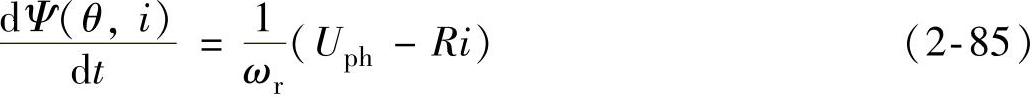
式中，Ψ、i、R分别为相绕组的（自感）磁链、电流及电阻；ω_r为转子机械角速度；U_ph为相绕组的外施电压，且若采用图2-33所示的不对称半桥主电路，对于APC运行方式，有

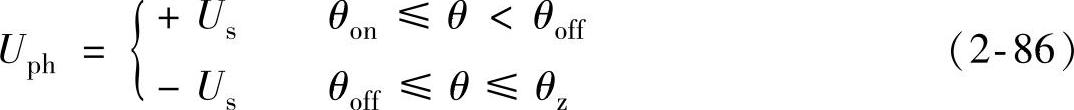
式中，θ_z为i_k降为零时的转子位置。

对于斩波运行方式，当θ_off≤θ＜θ_z时，仍有U_ph=-U_s。而在斩波工作区（θ_on≤θ＜θ_off），当相绕组导通时，U_ph=+U_s；当相电流斩波续流时，对于硬斩波，取U_ph=-U_s；对软斩波，则取U_ph=0。

在2.6节计算获得非线性磁化曲线族Ψ（θ，i）数据的基础上，任给一对（θ、Ψ），利用已知的Ψ（θ，i）数据，即可插值求取对应的i，从而可由给定的初始条件θ_t=0、i_t=0、Ψt=0，应用龙格-库塔法等数值积分方法求解式（2-85），得到SR电动机稳态运行时相电流的数值仿真结果。众所周知，四阶龙格-库塔法常用于高精度计算，其求解式（2-85）的算法为

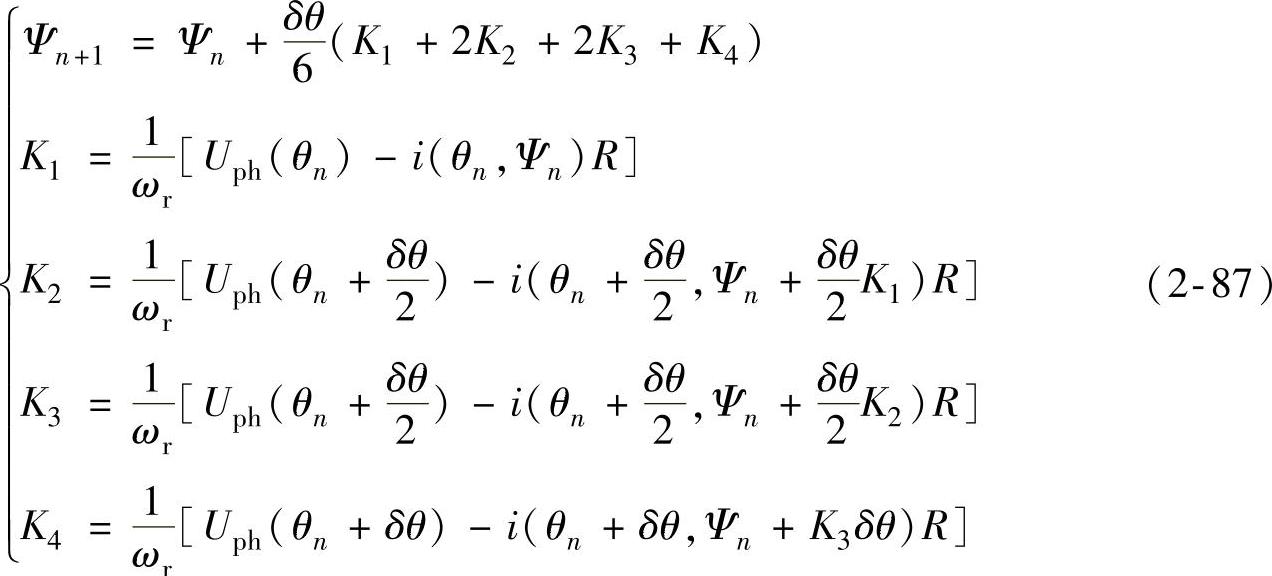
式中，n为迭代的步数；δθ为迭代步长，即转子位置角的增量，可根据不同的角速度取不同的值。

在求解式（2-85）过程中，由每一步迭代得到的i（θ），利用已知的电磁转矩特性T（θ，i）数据，即可插值求取对应的电磁转矩，从而得到稳态运行时电磁转矩的仿真结果。

图2-37～图2-39分别给出了样机1在CCC（采用硬斩波）、电压PWM（采用硬斩波）、APC方式下稳态运行的仿真结果。(www.xing528.com)

以上仿真利用已知的Ψ（θ，i）、T（θ，i）数据表格，采用插值和数值积分方法，避免了求导运算，既有较高的仿真精度又有较快的仿真速度。除了采用上述仿真方法，亦可利用3.6节中非线性磁链解析式和电磁转矩解析式进行快速数值仿真^[14，187]。

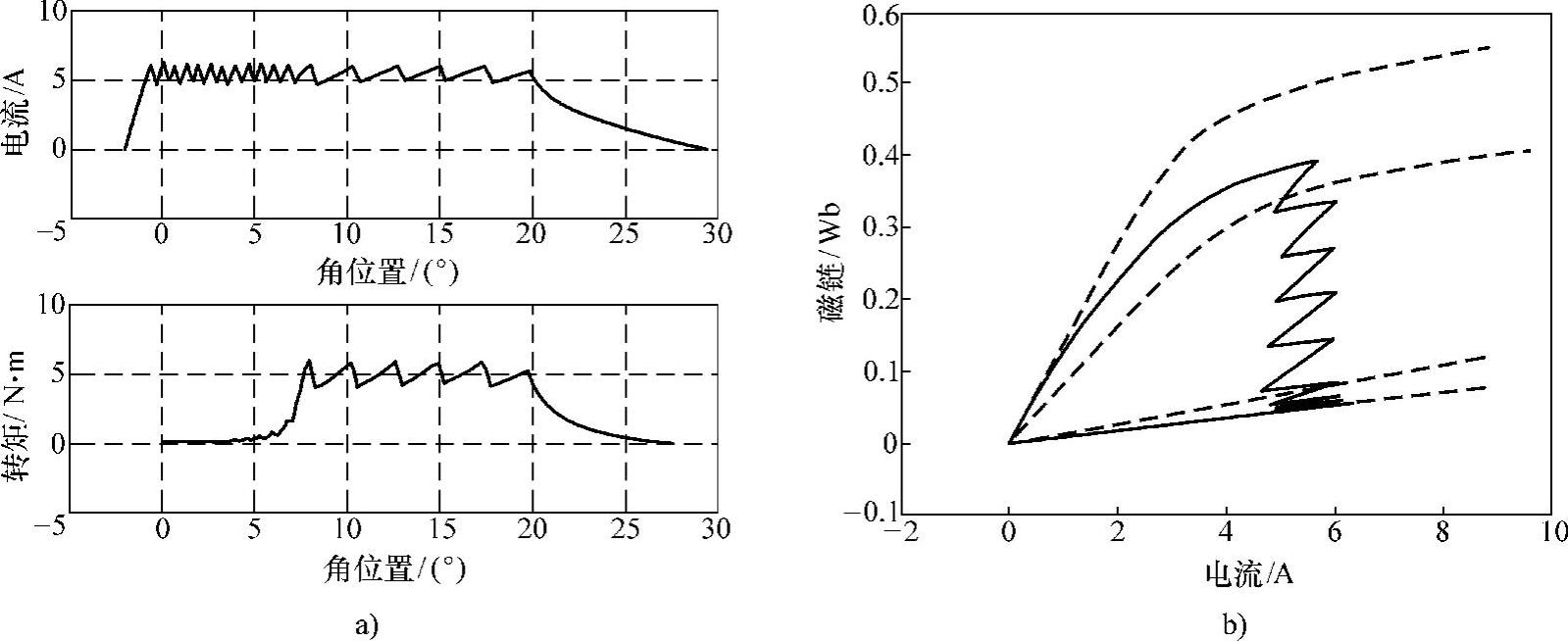
图2-37 CCC方式稳态运行仿真（转速为500r/min）

a）相电流（上）及电磁转矩（下） b）磁链-电流轨迹（虚线为四个特殊位置处的磁化曲线）

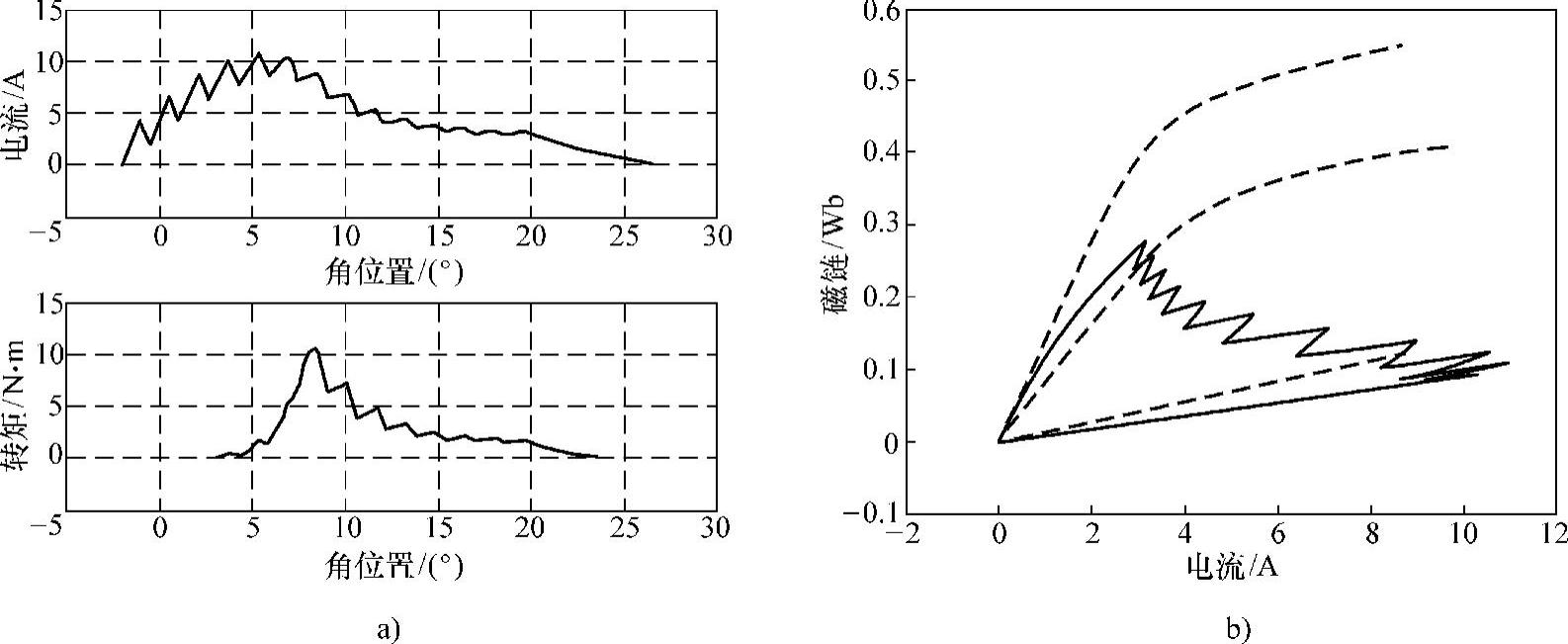
图2-38 电压PWM方式稳态运行仿真（转速为500r/min）

a）相电流（上）及电磁转矩（下） b）磁链-电流轨迹（虚线为四个特殊位置处的磁化曲线）

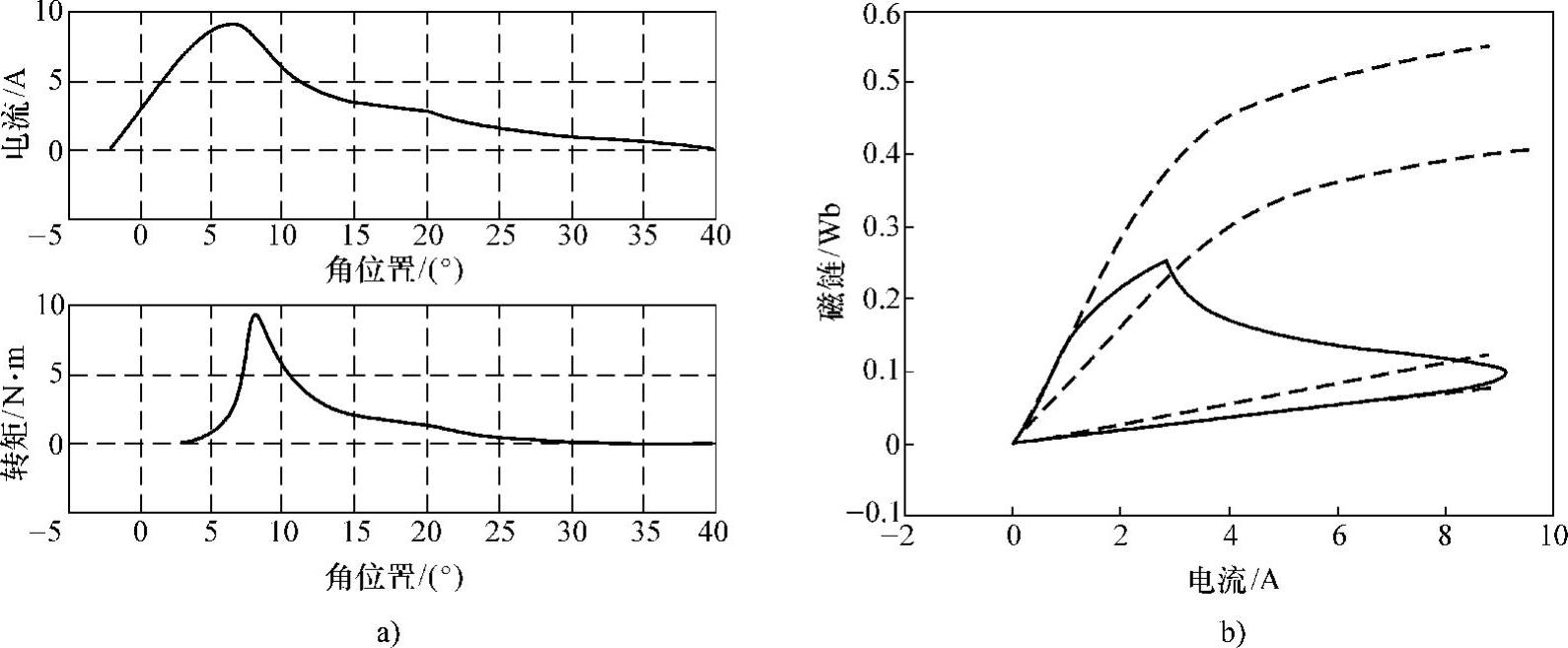
图2-39 APC方式稳态运行仿真（转速为1600r/min）

a）相电流（上）及电磁转矩（下） b）磁链-电流轨迹（虚线为四个特殊位置处的磁化曲线）