基本方法：2.5SR电动机调速控制

整理式（2-50），得

式（2-52）中的F代表一个繁琐的以电动机结构参数（m、N_r、θ₂、L_max、L_min）及控制参数（θ_on、θ_off）为自变量的函数式，对给定的电动机，F仅是控制参数的函数。

若U_s、θ_on、θoff恒定，由式（2-52）可得SR电动机的固有机械特性及输出功率分别为

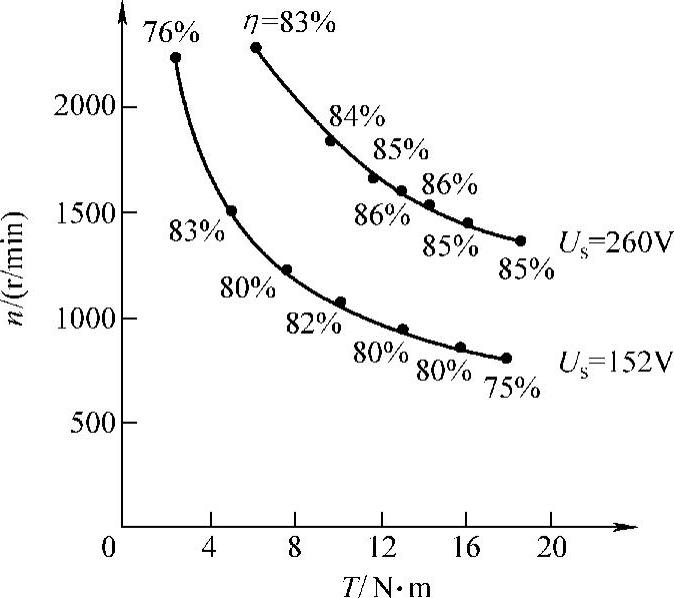
图2-18 SR电动机固有机械特性

可见，SR电动机具有类似于串励直流电动机的固有特性，对于不同的U_s，将对应不同的T_av-ω_r机械特性。作为示例，图2-18给出某四相（8/6极）2.2kW SR电动机在θ_on、θ_off分别固定为3°、18°，对应于不同U_s的机械特性（曲线上各点的数值为系统的效率），其形状类似于串励直流电动机的软机械特性。该特性曲线的上限对应于最高额定电压U_smax。对结构参数已确定的SR电动机，存在一个临界角速度ω_b，其对应于U_smax下的最大磁链Ψ_max和最大电流i_p，ω_b在参考文献[1]中被称为“基速（Base Speed）”，其是SR电动机能得到最大电磁转矩时的最高角速度，即能得到最大输出功率的最低角速度。

下面就多数传动装置所需的一种典型转矩-转速特性——从静止到基速具有恒转矩特性，在基速以上输出恒功率特性来研究SR电动机的两种基本控制策略。

1）基速ω_b以下，电流斩波控制（Chopped Current Control，CCC），输出恒转矩特性。

由式（2-47）、式（2-48）可知，Ψ_max及i_p随角速度ω_r的降低而增大，因此当SR电动机在基速以下运行时，应调节U_s、θ_on、θ_off这三个可控变量，使Ψ_max及i_p不超过允许值。若要在0～ω_b内获得恒转矩特性，则可固定θ_on、θ_off，通过斩波控制相绕组的励磁电压来达到。具体实现方法有两种。其一，如2.3.3节所述，用电流的限值来控制U_s加在导通相上的有效时间，改变限流幅值的大小，即可控制输出转矩变化，此法即为通常意义上的电流斩波控制（CCC），亦称为电流PWM控制；其二，用控制信号（如速度给定和实际速度之差经调节器后的输出信号）调制U_s加在导通相上的有效时间宽度来改变励磁电压的平均值，进而改变转矩，此法亦称为电压PWM控制。

式（2-52）表明，ω_r与励磁电压成正比，而式（2-17）、式（2-20）、式（2-34）表明，Ψ（θ）、i（θ）则正比于励磁电压与ω_r之比，因此当θ_on、θ_off固定，且负载转矩一定时，调节励磁电压，ω_r将随之变化，而Ψ（θ）、i（θ）波形的形状基本保持不变，只是频率发生变化。由此可见，斩波调速控制可使SR电动机在基速以下运行时的输出转矩基本上为常数，同时磁通基本保持不变，属于“恒转矩调速”性质。

2）基速ω_b以上，角度位置控制（Angular Position Control，APC），输出恒功率特性。

由式（2-17）、式（2-20）、式（2-34）及式（2-52）可知，在U_s、θ_on、θ_off一定时，随ω_r增加，Ψ或i将以ω_r^-1下降，T_av则“自然”地以ω_r^-2下降，但这种自然降落可通过按比例地增大导通角θ_c=θ_off-θ_on来补偿，这样可控制导通时间不以ω_r^-1下降，若做到使磁通以ω_r^-1/2下降，则转矩将受控制地随ω_r^-1下降，即可在一个较宽的速度范围内得到恒功率输出特性。(www.xing528.com)

图2-19为不同运行方式下实测的SR电动机相电流典型波形。

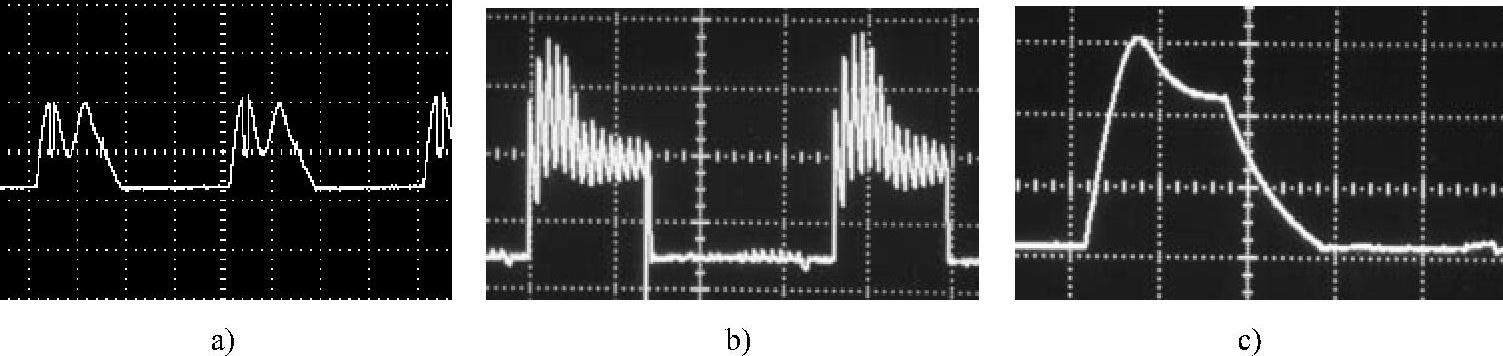
图2-19 不同控制方式下，实测的相电流波形

a）CCC方式 b）电压PWM方式 c）APC方式

由式（2-52）可知，采用APC调速方式时，对于给定的负载特性，其转速取决于θ_on、θ_off。θ_on、θ_off无解析解，但可用图解法确定，如图2-20所示。

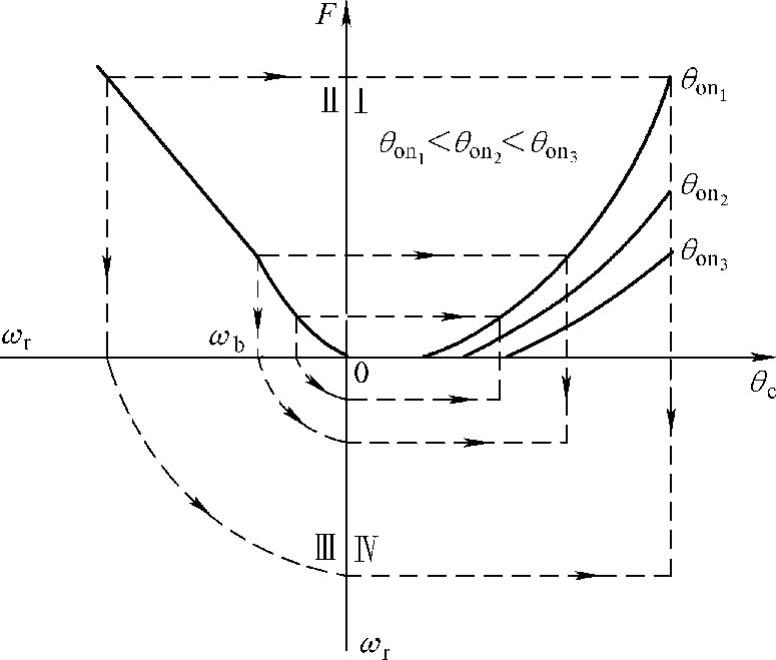
图2-20 APC方式图解[63]

图2-20中，象限Ⅰ中的F（已知一定几何尺寸的SR电动机）是在不同的开通角θ_on下相对于导通角θ_c（=θ_off-θ_on）画出的；象限Ⅱ中是针对ω_b以下恒转矩、ω_b以上恒功率的负载转矩/转速特性依式（2-52）画出的F相对ω_r的曲线。在象限Ⅳ中，纵轴为ω_r，横轴为θ_c，由式（2-18）可知，Ψ_max正比于θ_c/ω_r，因此在象限Ⅳ中，任一点的横坐标与纵坐标之比正比于Ψ_max。

在象限Ⅱ中，选择曲线上一点（即给定负载的某一运行转速点），由该点至象限Ⅰ作水平线，由该水平线与象限Ⅰ中F曲线的交点即可确定可能的θ_on、θ_off组合，进而确定象限Ⅳ中与这一开关角组合及运行速度相对应的Ψ_max。由图2-20可见，在基速ω_b（恒转矩区的最高转速）以下，Ψ_max随着ω_r的下降而上升；而在ω_b以上的恒功率区，Ψ_max则随ω_r的上升而下降，因此SR电动机的APC方式类似于直流电动机中减弱磁场的控制，基本上属于“恒功率调速”。

然而，导通角的增大是有限制的，一般不能超过τ_r/2，即U_s=U_smax、θ_c=θ_cmax=τ_r/2=π/N_r所对应的运行角速度ω_sc是APC方式的上限，若SR电动机超过ω_sc运行时，由于θ_on、θ_off已调到极限值，没有进一步调节的余地，这时SR电动机将回复到对应于θ_c=τ_r/2时的固有机械特性上运行，转矩不再随转速的一次方下降，而是与转速的二次方成反比，即呈串励特性运行，如图2-21所示。

在参考文献[11]中，将ω_b（最大功率下的最低转速）和ω_sc（最大功率下的最高转速）分别冠以“第一临界转速”和“第二临界转速”。显然，控制变量（U_s、θ_on、θ_off）的不同组合，两个临界点在速度轴上将对应不同的分布，并且在上述两个区域内分别采用不同的控制方法，便能得到满足不同需求的机械特性，这充分说明SR电动机具有十分优良的调速控制性能。

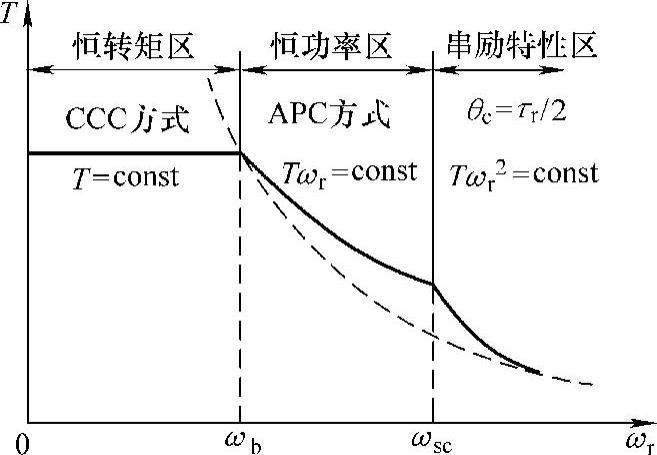
图2-21 SR电动机调速的控制特性