基于准线性模型的平均转矩计算

为推导简单起见，忽略所有功率损耗，假设主开关器件的切换是瞬时的，角速度ω_r恒定，且忽略互感磁链，这样各相绕组的作用可分别讨论。

SR电动机每转一圈，每相导通的单向电流脉冲数与转子极数N_r相同，故m相电动机每转对应mN_r个脉冲，即运动mN_r步。实际电流脉冲的形状随转矩、转速而变，为进一步简化分析，假设相电流为理想的平顶波电流，如图2-15所示。基于图2-13b所示的准线性模型的分段线性化磁化曲线，随图2-15所示的平顶波相电流变化，一相绕组对应磁链变化轨迹如图2-16所示。

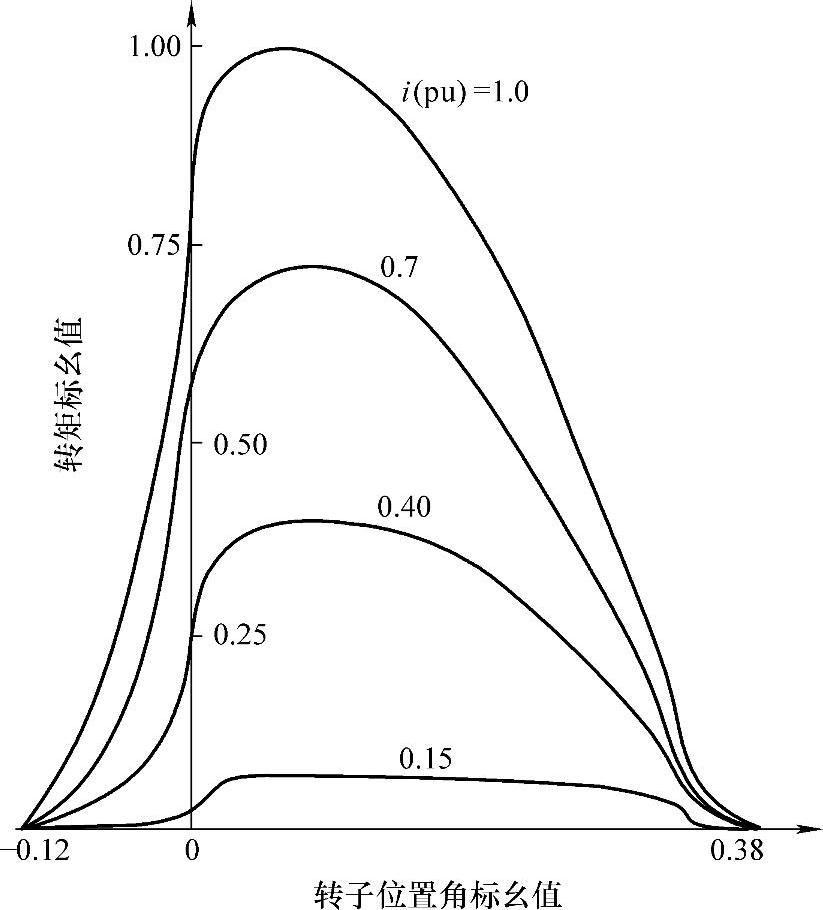
图2-14 瞬时转矩随转子位置角、相电流变化曲线^[1]

图2-16是基于如下假设作出的：

1）设当定子极与转子槽重叠时具有最小电感L_min，且为常数，所以对应电流由O点线性上升至A点，磁链Ψ由O点沿斜率L_min的直线线性上升至A点；

2）设当定、转子凸极中心线重合处的起始磁化曲线以L_max的斜率线性上升至D′点，当i＞i₁后，则以L_min的斜率变化，即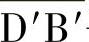平行于；

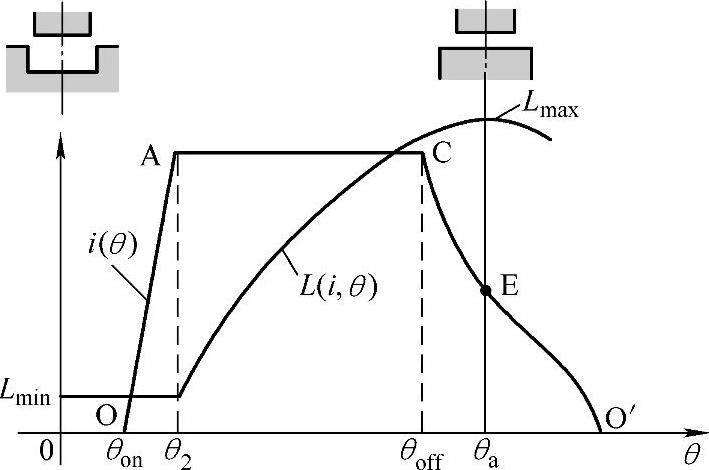
图2-15 SR电动机平顶波相电流（OACEO′）及电感曲线

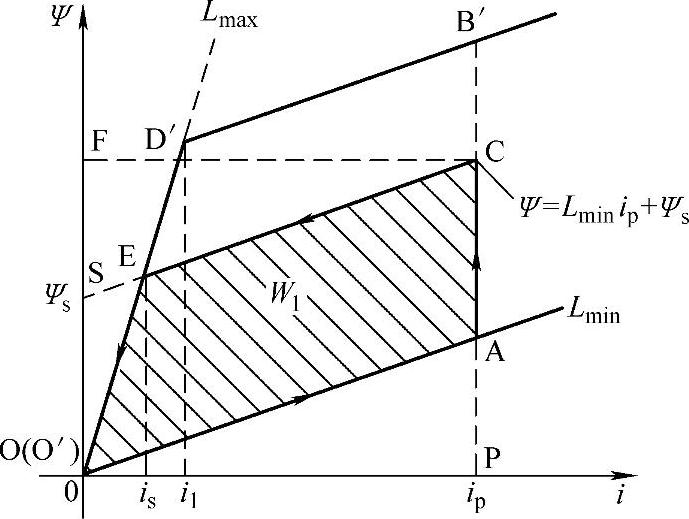
图2-16 SR电动机一相磁链-电流特性（OD′B′对应θ_a位置，OA对应定子极与转子槽重叠区域）

3）平顶电流结束时，工作点移至C点，该点即为换相点。换相开始后，电流逐渐下降，工作点沿斜率为L_min的直线下降至定、转子凸极中心线重合处的E点，E点的储能（三角形SEO面积）较C点（换相点）的储能小得多，且E点的电流i_s＜i₁，故可近似认为在进入电感下降区前电流已衰减至零，在E点后，随着续流电流的衰减，Ψ将沿着斜率为L_max的直线下降至零。

由机电能量转换原理可知，SR电动机每相在一个工作周期（转子角周期τ_r=2π/N_r）中的磁共能增量（即转变成机械功输出的有效电磁能量）W₁为电流变化一个周期内，Ψ/i平面各工作点所围闭合曲线的面积，即图2-16中有斜线的面积S_OACEO。若不计电阻损耗，则m相SR电动机的总平均电磁转矩为

已知电感参数、平顶波电流幅值i_p及外施直流电压U_s，即可解析计算面积W₁，由图2-16，得

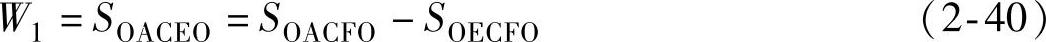
式中，S_OACFO为换相点C前，相绕组所接受的电源供能；S_OECFO为换相后续流阶段绕组回馈给电源的能量。

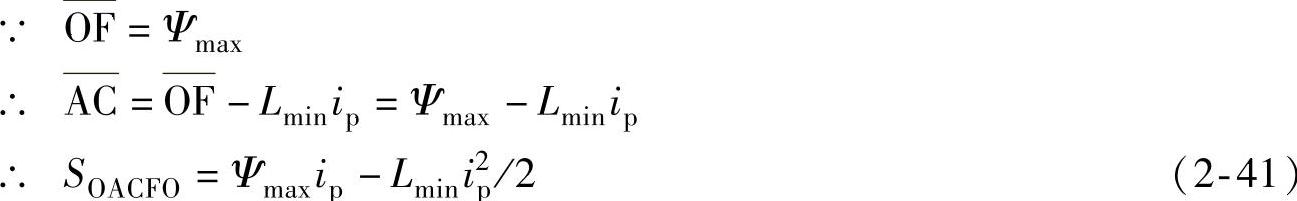
又 ∵S_OECFO=S_△CFS+S_△SEO

由图中几何关系，有

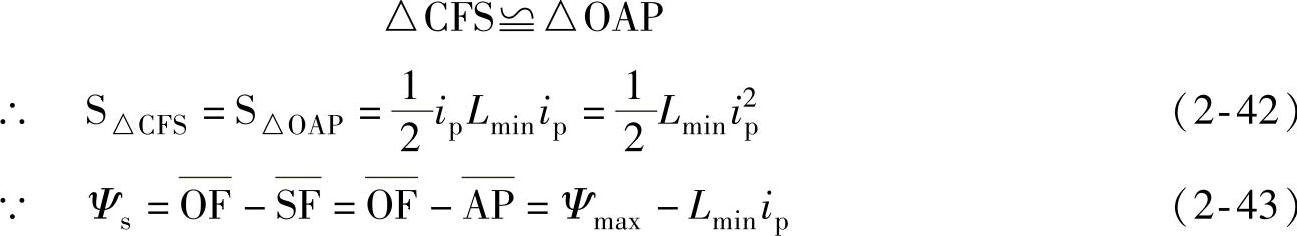(www.xing528.com)

又 ∵Ψ_s=（L_max-L_min）is

由式（2-43）、式（2-44），得

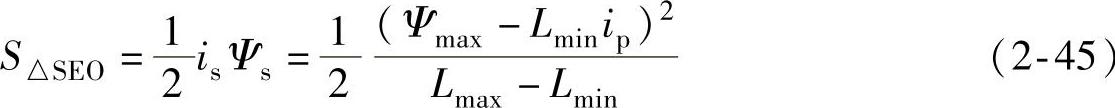
将式（2-41）、式（2-42）和式（2-45）代入式（2-40），得

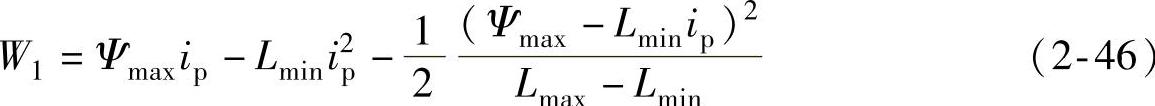
由式（2-17）、式（2-24）可分别求得Ψ_max、i_p，即有

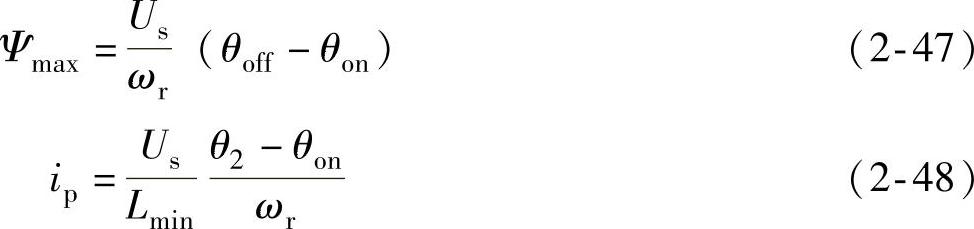
将式（2-47）、式（2-48）代入式（2-46），得

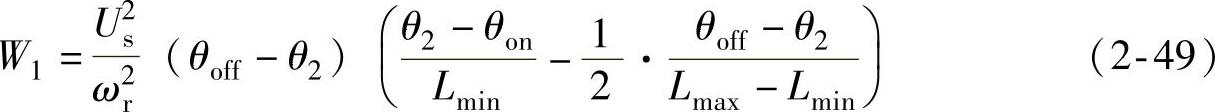
将式（2-49）代入式（2-39），即得m相SR电动机的总平均电磁转矩解析式为

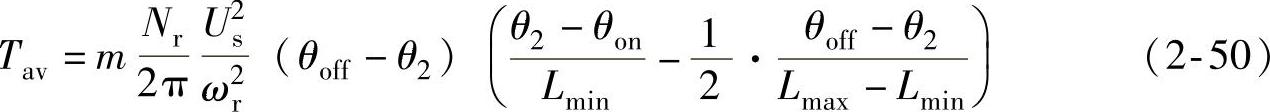
若不计空载损耗，m相SR电动机的输出功率为

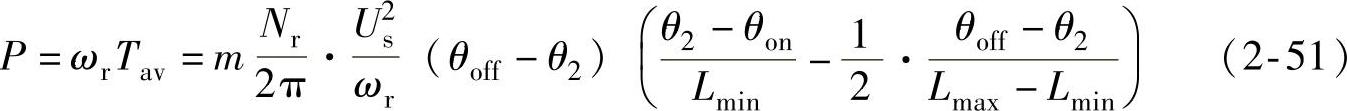
由式（2-50）可定性说明SR电动机的基本转矩特性及其随各种参数而变的趋势：

1）L_max/L_min值越大，每一工作周期内所能获得的有效电磁能量W₁的最大值亦越大，电磁转矩亦越大，这一点在第3章中将进一步讨论。应该指出，在式（2-50）中，是以L_max和L_min之差影响电磁转矩的，当L_max/L_min值已经较大时，再增大L_max/L_min，Tav的增大并不显著，而要进一步提高L_max/L_min值，在技术、经济上均要付出代价。因此，在SR电动机设计中，通常以选L_max/L_min=6较为合适。

2）在角速度ω_r一定时，若开通角θ_on较小时，相电流在最小电感区域上升的时间（θ₂-θ_on）/ω_r较长，从而增大进入有效工作区的电流，提高输出转矩，因此θ_on是控制电磁转矩的重要参数。在θ_on一定时，增大关断角θ_off，W₁增大，则平均转矩相应增大。但关断角θ_off有一最佳值，超过此值后，随θ_off增大，T_av反而减小。实际上，θ_off的增大，不仅使dL/dθ＞0的有效工作区域内的平均电流增加，从而导致电动转矩增大，但同时亦有可能使流过dL/dθ＜0区域的平均电流增加，从而引起制动转矩增加。因此，θ_off必有一个最佳值，当关断角大于该值，制动转矩的增值超过电动转矩的增值，平均转矩开始下降。

图2-17给出SR电动机的平均电磁转矩T_av随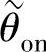、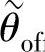变化的实例，其中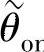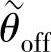，、均用以转子角周期τ_r作为基值的标幺值表示。

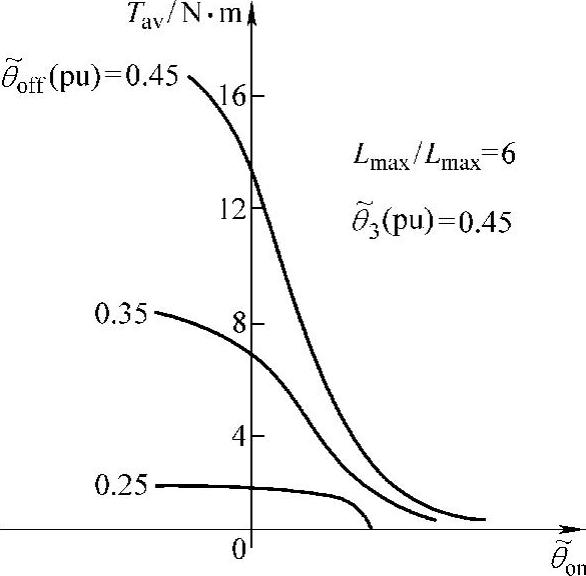
图2-17 平均电磁转矩随开通角、关断角变化