SR电动机准线性模型分析与优化

由于磁路的非线性、磁通的复杂分布及相间的非线性耦合等因素，SR电动机的电磁转矩难以准确解析计算。如何在满足工程准度要求的前提下，简化SR电动机电磁转矩计算是SRD理论研究中的重要课题之一。

式（2-6）表明，SR电动机的电磁转矩等于磁路系统的磁共能W′对转子位置θ的偏导数。而磁共能是相电流i、转子位置角θ或相绕组磁链Ψ与θ的函数，因此Ψ-i-θ关系曲线是SR电动机电磁转矩计算的基础。实际上，各种简化模型及其对应的转矩计算近似公式^[11，14]的区别正在于对实际非线性Ψ-i-θ关系曲线所作的不同简化处理。

2.3节中，忽略磁路饱和影响，设相电感不随电流变化所建立的线性模型中，对一定的转子位置角θ，Ψ=L（θ）i（θ）为一条直线，即将一定转子位置角对应的Ψ=f（i）曲线近似成直线，如图2-12所示。

参考文献[19]基于SR电动机线性模型获得的相电流解析式，计算转子转过一个转子极距角τ_r时，系统磁共能的改变量（即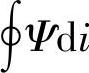（）/τ_r），导出平均转矩解析式，为SR电动机设计时结构参数初选及控制参数的选择与匹配提供了重要的理论指由。但是，SR电动机实际工作的磁路是饱和的，电感实际上是转子位置θ和相电流i的非线性函数。磁路饱和对电磁转矩、功率的分析与计算有显著影响，应予以充分考虑。但若不加简化地考虑磁路的非线性，使用图2-13a所示的实际非线性磁化曲线，则使得电磁关系计算十分困难，且难以解析计算。

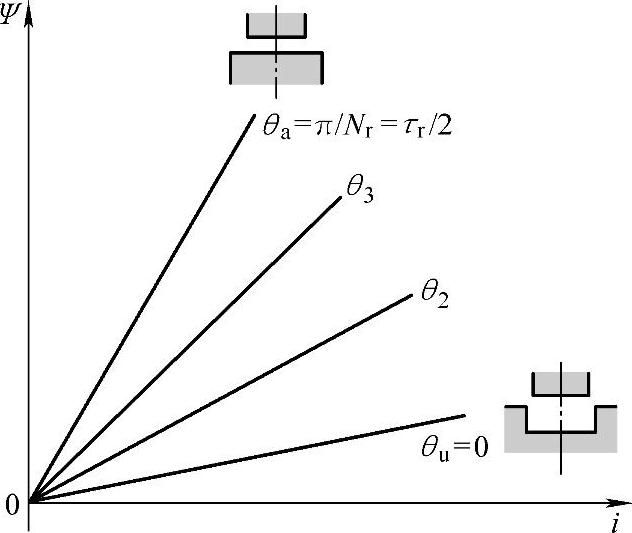
图2-12 基于线性模型的SR电动机磁化曲线

实用中，为避免繁琐的计算，又不失一定的工程精度要求，常采用“准线性模型”近似计及磁路的饱和效应，即将实际的非线性磁化曲线分段线性化，同时不考虑相间耦合效应，作这样的近似处理后，每段磁化曲线均可解析。

分段线性化的方法有多种。图2-13b给出SR电动机性能分析中常用的一种准线性模型的磁化曲线，即用两段线性特性来近似图2-13a所示的一系列实际的非线性磁化曲线。其中一段为磁化特性的非饱和段，其斜率为电感L（θ，i）的不饱和值；另一段为磁化特性的饱和段，可视为与θ=0（磁阻最大位置）处的非饱和特性平行，斜率为L_min，图中的i₁，是根据θ=θ_a位置即定转子凸极对准时的磁化曲线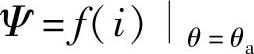决定的，一般定在其磁化曲线开始弯曲处。(www.xing528.com)

基于图2-13b的SR电动机准线性模型的分段线性化磁化曲线，可写出相电感的分段解析式（注意与线性模型式（2-9）比较）为

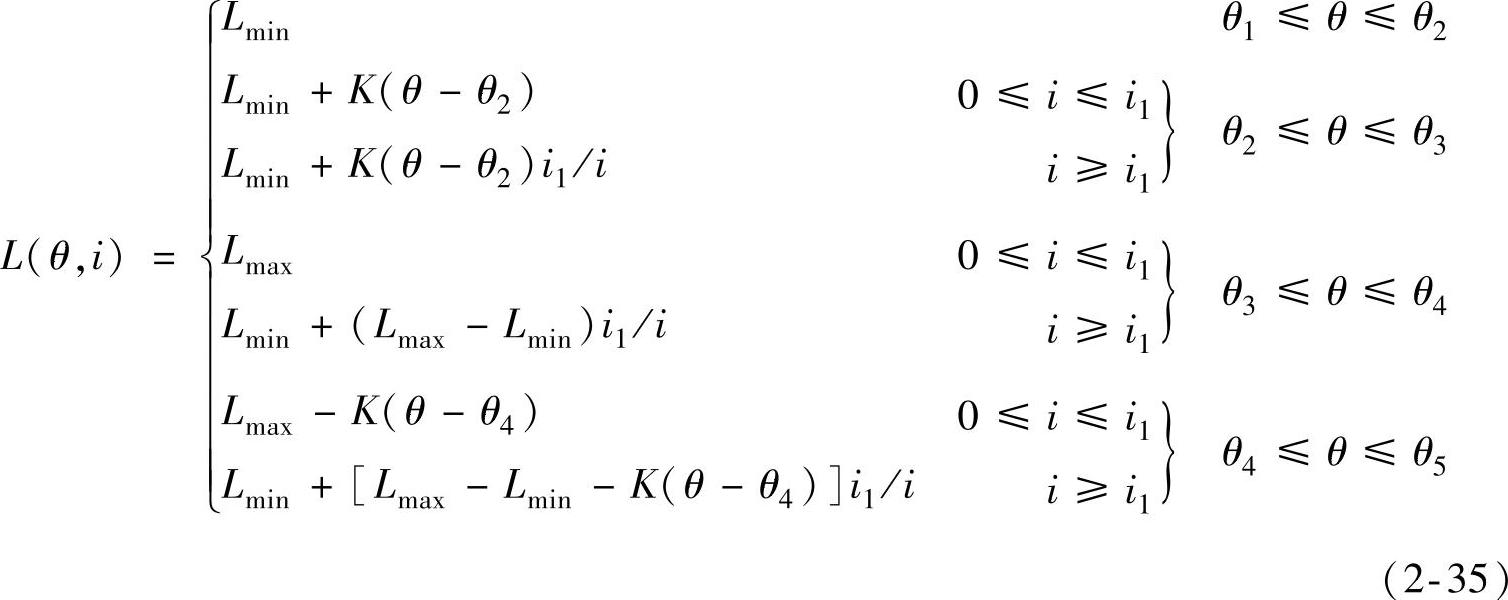
式（2-35）中各变量的含义与式（2-9）中相同。

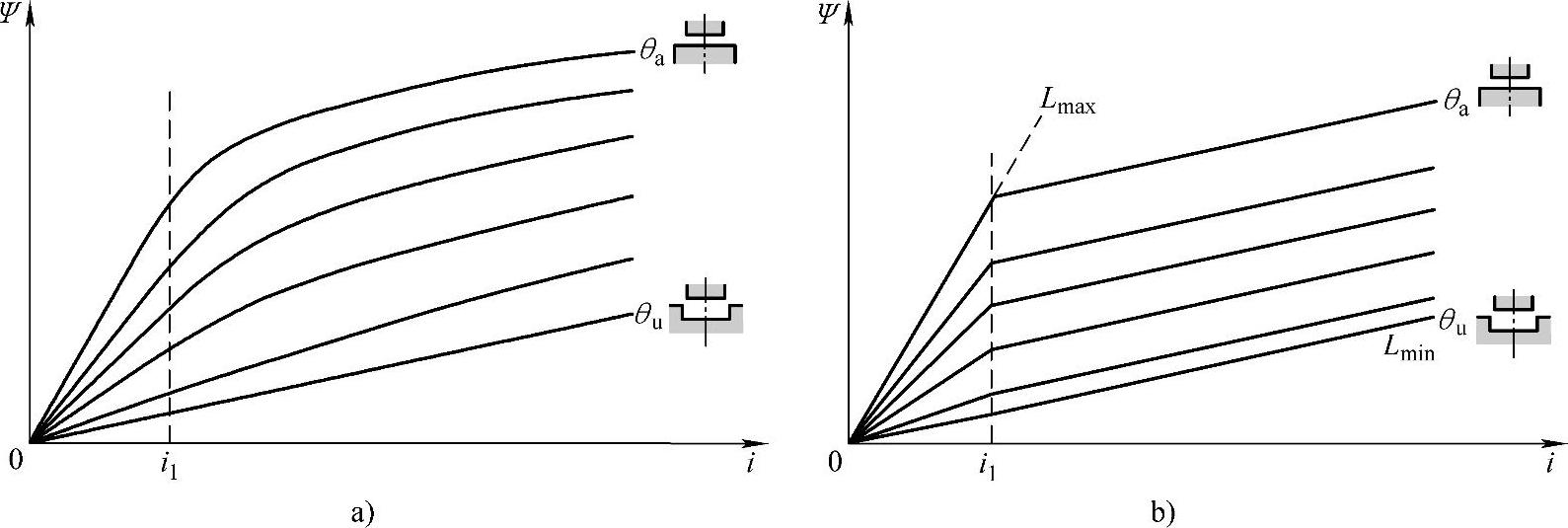
图2-13 实际非线性磁化曲线与准线性模型的分段线性化磁化曲线

a）实际非线性磁化曲线 b）准线性模型的分段线性化磁化曲线