机电联系方程的表达式

按机电能量转换原理，SR电动机同样通过耦合磁场的作用产生了两个机电耦合项，即电端口的感应电动势和机械端口的电磁转矩。SRD是一种调速系统，按电机统一理论，调速的关键是转矩控制，因此，电磁转矩计算是SRD动态性能分析及SR电动机、功率变换器、控制器设计的必要基础。

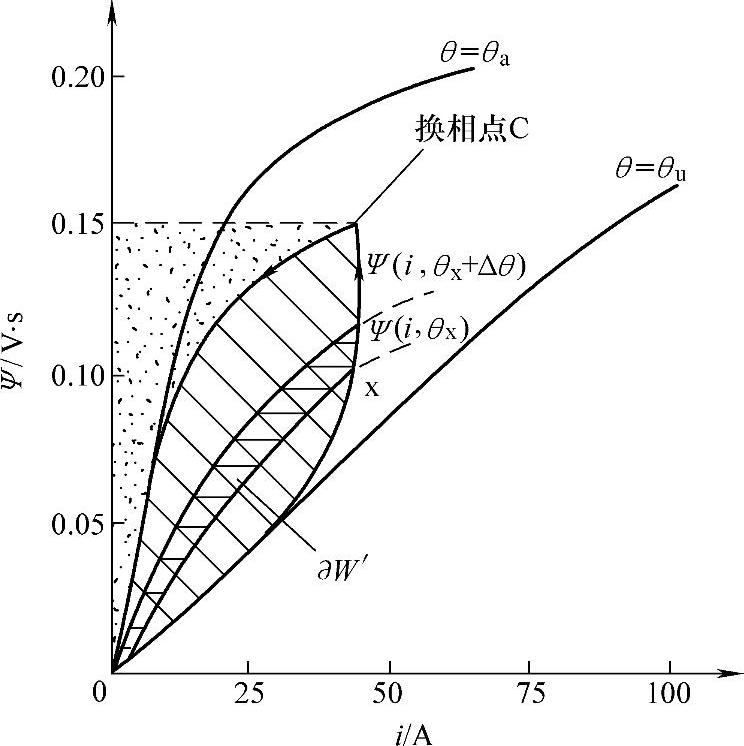
SR电动机一相绕组在一个工作周期（即转子角周期）中的机电能量转换过程可通过其在磁链-电流（Ψ-i）坐标平面的轨迹加以完整描述。磁路适当饱和对于高性能的SRD十分重要，而Ψ-i特性对理解系统在非线性磁化区的工作特性特别有用。实际上，SR电动机的静态性能可用随转子位置θ和相电流周期性变化的磁链Ψ（θ，i）曲线来表征。图2-3为某5hp（3.73kW）SR电动机采用角度位置控制方式的相电流，图2-4为对应的相绕组在Ψ-i平面上运行点的轨迹^[3]。该轨迹一般介于两条特殊角度位置处的磁化曲线内，这两条特殊磁化曲线分别对应于定转子凸极中心线重合的最小磁阻位置θ_a和定子凸极中心与转子凹槽中心线重合的最大磁阻位置θ_u。

因忽略相绕组间互感，故可从一相入手考察SR电动机的电磁转矩。如图2-4所示，每相在一个工作周期内输出的机械能为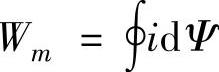，即为运行轨迹所包围的面积（图中有斜线的区域）。在任一运行点x处的瞬时电磁转矩根据虚位移原理，得

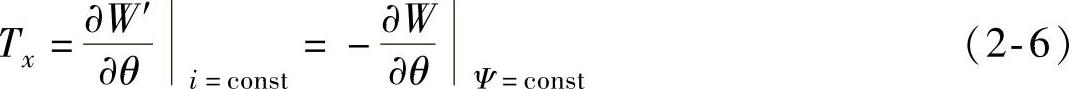
式中，W′为绕组的磁共能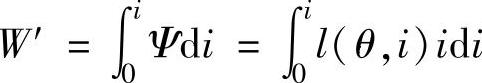，；∂W′即为耦合磁场在转子位移增量Δθ内的磁共能增量；W为绕组的储能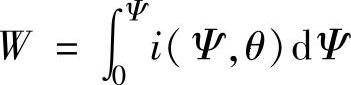，。在Ψ-i平面上，任一运行点处储能大小即为该点所对应转子位置处的磁化曲线以左的区域面积。图2-4中有点的区域面积即为运行点C处绕组的磁能。C点为换相点，其时绕组的主开关器件关断，绕组电流开始下降。

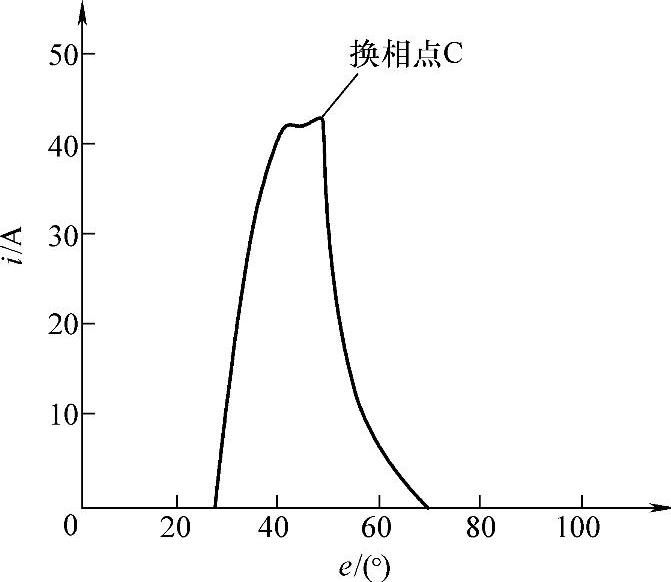
图2-3 5hp SR电动机角度位置控制方式相电流^[3]

(www.xing528.com)

图2-4 5hp SR电动机Ψ-i轨迹

图2-4表明，在磁路饱和状态下运行的SR电动机是一种强非线性的机电装置，表示储能W和磁共能W′的积分难以解析计算，且储能W和磁共能W′不可能相等。

因电动机及负载均有一定的转动惯量，决定电动机出力及动态特性的往往是平均转矩，因此平均转矩计算是SRD分析、设计的重要依据。

对式（2-6）在一个工作周期内积分并取平均，且基于各相绕组对称的假设，得SR电动机平均电磁转矩为

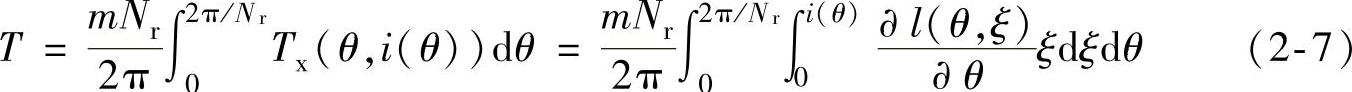
式中，m为SR电动机的相数；N_r为转子凸极数。

式（2-4）～式（2-6）（或（2-7））一并构成SR电动机的数学模型，尽管该模型从理论上完整、准确地描述了SR电动机中的电磁及力学关系，但由于l（θ，i）及i（θ）难以解析，故很难实际应用，应根据研究的目的和所要求的准确程度进行合理的简化。一般根据对非线性相电感（或磁链）近似处理方法不同，分为线性模型、准线性模型、非线性模型。线性模型突出了SR电动机的基本物理特性，可避免繁琐的数学推导，适用于初步设计和定性分析；准线性模型计及饱和的影响，对线性模型进行适当修正，提高了建模精度，又不失物理概念清晰的优点，可用于功率变换器及控制策略的分析与设计；非线性模型精度最高，多用于SR电动机设计与性能分析、SRD整体非线性动态仿真建模及优化设计。