气相色谱的塔板理论与效能评价

1.塔板理论

在色谱分离技术发展的初期，人们将色谱分离过程比拟为化工生产过程中的蒸馏过程，因而直接引用处理蒸馏过程的概念、理论和方法来处理色谱过程，即将连续的色谱过程看作是许多小段平衡过程的重复。这个半经验的理论把色谱柱比作一个蒸馏塔，色谱柱可由许多假想的塔板组成（即色谱柱分成许多个小段），在每一小段（塔板）内，组分分子依据自身的分配系数在两相间进行分配。由于流动相在不停地移动，因此组分就在这些塔板间隔的气、液两相间不断地达到分配平衡。塔板理论假定：

1）在这样一小段间隔内，气相平均组成与液相平均组成可以很快地达到分配平衡。这样达到分配平衡的一小段柱长称为理论塔板高度H。

2）载气进入色谱柱，不是连续的而是脉动式的，每次进气为一个板体积。

3）试样开始时都加在第0号塔板上，且试样沿色谱柱方向的扩散（纵向扩散）可略不计。

4）分配系数在各塔板上是常数。

根据塔板理论，塔板数n、塔板高度H和塔高（在此即色谱柱柱长）L之间的关系为

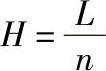
由于色谱柱的塔板数相当多，因此性质极其相似的两组分也能获得好的分离效果。

根据塔板理论还可导出塔板数n的计算公式为

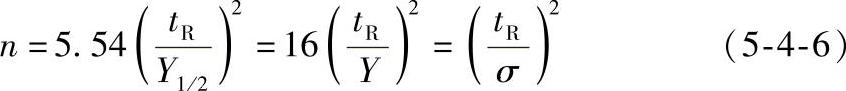
式中 n——理论塔板数；

Y_1/2——半峰宽（以时间为单位）；

Y——峰宽（以时间为单位）；

t_R——组分保留时间。

由式（5-4-6）可见，色谱峰越窄，塔板数n越多，理论塔板高度H就越小，此时柱效能越高，因而n或H可作为描述柱效能的一个指标。

由于死时间t_M（或死体积V_M）的存在，它包括在t_R中，而t_M（或V_M）不参加柱内的分配，所以往往计算出来的n很大，H很小，但色谱柱表现出来的实际分离效能却并不好，特别是对流出色谱柱较早（t_R较小）的组分更为突出。因而理论塔板数n和理论塔板高度H并不能真实反映色谱柱分离的好坏。为此，提出了将t_M除外的有效塔板数n_有效和有效塔板高度H_有效的概念，并将其作为柱效能指标。

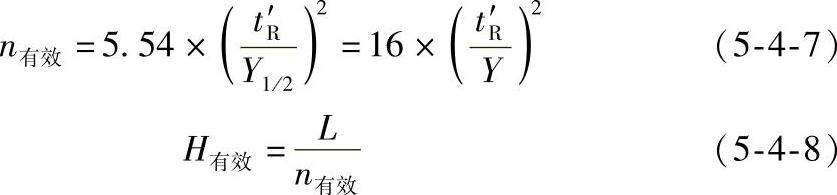
式中 n_有效——有效塔板数；

H_有效——有效理论塔板高度；

Y_1/2——半峰宽（以时间为单位）；

Y——峰宽（以时间为单位）；

t_R′——组分调整保留时间。

应该指出，同一色谱柱对不同物质的柱效能是不一样的，当用这些指标表示色谱柱效能时，必须说明是对什么物质而言的。

塔板理论在解释色谱流出曲线的形状（呈正态分布）、浓度极大点的位置以及计算评价色谱柱效能等方面都取得了成功。但是它的某些基本假设是不当的，例如纵向扩散是不能忽略的，分配系数与浓度无关，只在有限的浓度范围内成立，而且色谱体系几乎没有真正的平衡状态。因此，塔板理论不能解释塔板高度受哪些因素影响这个本质问题，也不能解释为什么在不同流速（F）下可以测得不同的理论塔板数这一试验事实，如图5-4-6所示。尽管如此，由于以n或H作为色谱柱效能指标很直观，因而迄今仍为色谱工作者所接受。

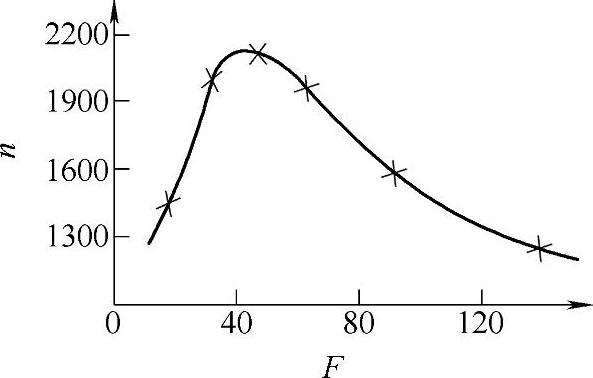
图5-4-6 流速对塔板数的影响

2.速率理论(www.xing528.com)

1956年，荷兰学者范弟姆特（Van Deemter）等提出了色谱过程的动力学理论。他们吸收了塔板理论的概念，并把影响塔板高度H的动力学因素结合进去，导出了塔板高度H与载气流速u的关系，即为范弟姆特方程式的简化式。

式中 A——涡流扩散项；

B——分子扩散系数；

C——传质阻力系数。

其中，A、B、C为三个常数。影响板高H的三项因素为：涡流扩散项、分子扩散项和传质阻力项。

（1）涡流扩散项A

A=2λd_p

即A与填充物的平均颗粒直径d_p（单位为cm）和填充的不均匀性λ有关，而与载气性质、线速度和组分无关。因此，使用适当细粒度和颗粒均匀的担体，并尽量填充均匀，是减少涡流扩散，提高柱效能的有效途径。对于空心毛细管柱，A项为零。

（2）分子扩散项（又称为纵向扩散项）B/u

B=2γD_g

式中 γ——因载体填充在柱内而引起气体扩散路径弯曲的因数（弯曲因子）；

D_g——组分在气相中的扩散系数（cm²/s）。

纵向扩散与组分在色谱柱内的保留时间有关，保留时间越长（相应于载气流速越小），分子扩散项对色谱峰扩张的影响就越显著。分子扩散项还与组分在载气流中的分子扩散系数D_g成正比，而D_g与组分及载气的性质有关。相对分子质量大的组分，其D_g小。D_g反比于载气密度的平方根或载气相对分子质量的平方根，所以采用相对分子质量较大的载气（如氮气），可使B项降低。D_g随着柱温增高而增加，但反比于柱压。

弯曲因子γ为与填充物有关的因素。它的物理意义可理解为：由于固定相颗粒的存在，使分子不能自由扩散，从而使扩散程度降低。对于空心毛细管柱，γ=1；在填充柱中，由于填充物的阻碍，使扩散路径弯曲，扩散程度降低，γ＜1。

（3）传质阻力项CuCu包括气相传质阻力项C_gu和液相传质阻力项C_lu。

所谓气相传质过程，是指试样组分从气相移动到固定相表面的过程。在这一过程中，试样组分将在两相间进行质量交换，即进行浓度分配。这种过程若进行得缓慢，则表示气相传质阻力大，将引起色谱峰扩张。对于填充柱，气相传质系数C_g为

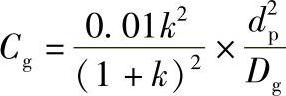
式中 k——容量因子。

由此可见，气相传质阻力与填充物粒度的二次方成正比，与组分在载气中的扩散系数成反比。因此，采用粒度小的填充物和相对分子质量小的气体（如氢气）作载气可使C_g减小，从而可提高柱效能。

液相传质阻力系数C_l为

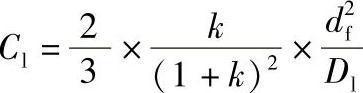
若固定相的液膜厚度d_f小，组分在液相中的扩散系数D_l大，则液相传质阻力就小。

对于填充柱，固定液含量较高（早期固定液的体积分数一般为20%～30%）。中等线速时，塔板高度的主要控制因素是液相传质阻力项，而气相传质阻力项数值很小，可以忽略。然而随着快速色谱的发展，在用低固定液含量柱和高载气流速进行快速分析时，C_g对H的影响不但不能忽略，而且会成为主要控制因素。

将常数项的关系式代入简化式中可得

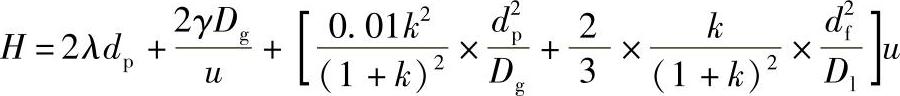
至此可见，范弟姆特方程式说明了固定相颗粒填充的均匀程度、担体的粒度、载气的种类、载气流速、柱温、液体固定相的液膜厚度等对柱效能和峰扩张的影响。因此，它对于色谱分离条件的选择具有理论上的指导意义。