基尔霍夫电压定律：电路分析的基本法则

基尔霍夫电压定律又叫做回路电压定律（简称为KVL），它说明在一个闭合回路中各段电压之间的关系。

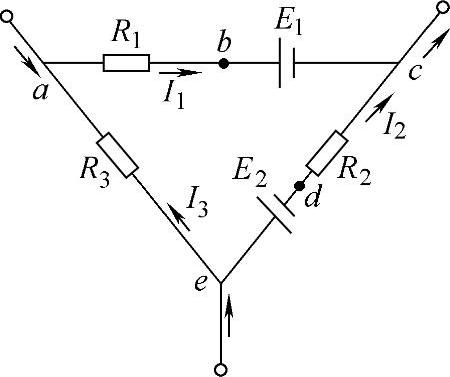
图2-19 回路

如图2-19所示，回路abcdea表示复杂电路若干回路中的一个回路（其他部分没有画出来），若各支路都有电流（方向如图所示），当沿a-b-c-d-e-a绕行时，电位有时升高，有时降低，但不论怎样变化，当从a点绕闭合回路一周回到a点时，a点电位都不变，也就是说，当从一点出发绕回路一周回到该点时，各段电压（电压降）的代数和等于零，这一关系叫做基尔霍夫电压定律，即

∑U=0 （2-16）

对于图2-19所示的电路，有

U_ae=R₁I₁+E₁

U_ce=-^R₂I₂-E₂

U_ea=R₃I₃

沿整个闭合回路的电压应为

U_ac+U_ce+U_ea=0(https://www.xing528.com)

即

R₁I₁+E₁-R₂I₂-E₂+R₃I₃=0

移项后得

R₁I₁-R₂I₂+R₃I₃=-E₁+E₂

上式表明：在任一时刻、任意一个闭合回路中，各段电阻上电压降的代数和等于各电源电动势代数和，公式为

∑RI=∑E （2-17）

这就是基尔霍夫电压定律的另一种形式。

在运用基尔霍夫电压定律所列的方程中，电压与电动势均指的是代数和，因此，必须考虑正、负。应该指出的是，在用式∑U=0（电压、电动势均集中在等式一边）时，各段电压的正、负号规定完全与本章2.5节中所述一样；但如果用∑RI=∑E（电压与电动势分别写在等式两边）时，电压的正、负规定就仍与前面相同，而电动势的正、负号则恰好相反，也就是当绕行方向与电动势的方向（由负极指向正极）一致时，该电动势为正；反之，为负。这是因为在式∑U=0中，电动势是作为电压来处理的，而在∑RI=∑E中，则是作为电动势来处理的。

在列方程式时，可以任意选择回路绕行方向，但一经选定后就不能中途改变。