使用X射线测定方法进行应力分析

GB/T 7704—2008《无损检测F射线应力测定方法》是测定残余应力的各种方法中唯一制定了国家标准的方法，符合国标试验条件的测量数据应是可信的。它是热处理淬火残余应力测定最常用的方法。

8.3.3.1 晶体弹性应变的微观模型

晶体中晶格格点上的粒子（原子、离子等）都是规则地周期性排列的，它们处于结合力场位能的最低位置，即平衡位置。当宏观应力作用到晶体上时，只是使规则排列的格点位置均匀发生变化（在拉伸方向被拉长、在其垂直方向被压短）。此变化量与作用应力成正比，符合弹性力学的胡克定律。其模型如图8-22所示。

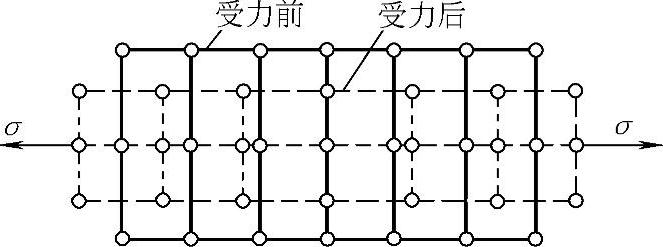
图8-22 晶体弹性变形的微观模型

图中每一列原子其实都是一个格点平面，我们称为晶面，这时格点间的距离称为晶面间距d，我们就用应力作用下的晶面间距的相对变化量作为残余应力作用下的弹性应变ε，所以根据胡克定律就有

ε=（d-d₀）/d₀=Δd/d₀ （8-24）

σ=Kε=K（Δd/d₀） （8-25）

式中 d₀——无应力时的晶面间距；

d——有应力时的晶面间距；

K——弹性常数。

由于晶体是各向异性的，所以不同晶面族的d值不同，其弹性常数也不同。此处宏观统计的弹性模量E值不能在此直接使用。

8.3.3.2 微观应变的X射线测定

从上述可知，宏观应变的测定已变为微观的晶面间距的变化量Δd的测定。据F射线在晶体上的衍射规律，有下述布拉格方程存在：

2dsinθ=nλ（n=1，2，…） （8-26）

d=nλ/（2sinθ） （8-27）

将上式两边求微分得

Δd/d=-cotθΔθ （8-28）

当Δd＜＜d时，d≈d₀，cotθ≈cotθ₀，代入式（8-28），有

Δd/d₀=-cotθ₀Δθ（8-29）式中的d₀、θ₀为无应力时的晶体某晶面族的晶面间距和衍射角，而Δθ为有应力衍射角θ与无应力时的衍射角θ₀之差。从式（8-29）可知，θ₀越趋于90°，则Δθ的测量误差对应变Δd/d₀的影响越小。所以一般θ₀在可能条件下尽量取最大值。因此，在测α-Fe的应力时，常用纯金属Cr制阳极（称铬靶）的F射线管产生的CrK_α特征F射线，其波长为0.229nm，其在α-Fe（211）晶面的衍射线的衍射角为θ₀=78°21′，这是衍射角最大的衍射。

8.3.3.3 物体表面残余应力的测定

1.表面任意点任意方向正应力的测定F射线穿透到物体内其强度按指数规律衰减，取入射线衰减到原始强度的千分之一时的深度为有效穿透深度，超过此深度的F射线衍射忽略不计。入射线为CrK_α（λ=0.229nm）时，对于α-Fe，其穿透深度为8μm；若用钴靶F射线的CoK_α（λ=0.179nm）入射时，其穿透深度为15μm。这个层深对于一般工件而言是最表层。一般在此层深内的残余应力可认为是沿层深均匀分布无梯度的。最表层应力的特点是在法线方向（一般取为Z方向）变形不受约束，而只在平面上（x、y方向）受约束。因此有σ_z=0，τ_xy=τ_yx=0，即表面处于平面应力状态。同样主应力中的σ₃也为零。

设物体表面为平面P，如图8-23所示。O点为欲测点，σφ为欲测方向上的残余应力。令O点的主应力为σ₁和σ₂，而欲测应力σφ与σ₁的夹角为φ，与各正应力对应的正应变为ε₁、ε₂和ε_φ。通过ε_φ作与表面垂直的截面（图8-24）。

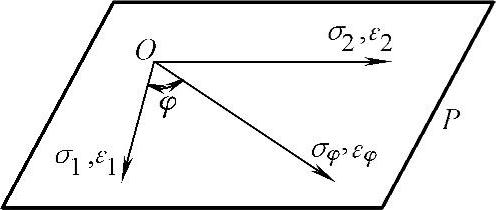
图8-23 表面应力示意图

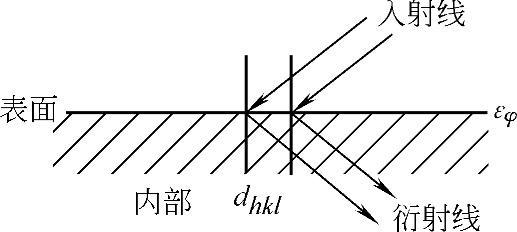
图8-24 ε_φ的X射线测定示意图

ε_φ可用与其相互垂直的某（hkl）晶面的面间距d_hkl的变化Δd/d₀来表示。从图8-24可知，不管采用何种入射线波长和晶面，其衍射线都只射向晶体内部，这样用探测器测不到衍射线，因此也就测不出衍射角θ和衍射晶面的面间距d以及应变ε_φ。为解决此问题，在物体表面（图8-25）过σ_φ作与平面P的垂直面，在此垂直面上过O点取与主应变ε₃成ψ角方向上的应变ε_ψ、φ。这个应变是可用F射线测出的。在图8-26中显示了这时衍射几何关系。只要衍射角θ足够大，ψ角足够小，衍射线就可射出物体表面，其衍射角θ_ψ、φ即可测定，据布拉格方程[式（8-26）]，即可求得d_ψ、φ，而ε_ψ、φ=Δd/d₀=（d_ψ、φ-d₀）/d₀，若将ε_ψ、φ与主应变ε₁、ε₂的关系转换成ε_ψ、φ与ε_φ的关系，就可以从测定的ε_ψ、φ求出ε_φ和σ_φ。

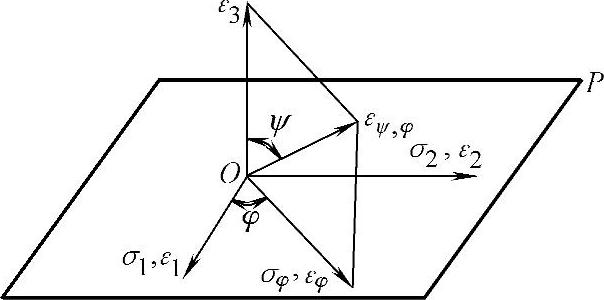
图8-25 表面应力的测定

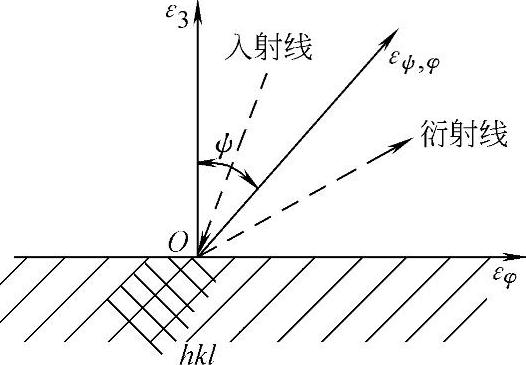
图8-26 ε_ψ、φ的X射线测定

根据弹性力学理论，若任一应变ε_ψ、φ与主应变ε₁、ε₂、ε₃的夹角分别为α、β、γ，则它们之间有如下关系：

ε_ψ、φ=ε₁cos²α+ε₂cos²β+ε₃cos²γ（8-30）由于ε_ψ、φ在平面P上的投影与ε_φ同方向，所以它与ε₁的夹角α就是φ，与ε₂的夹角β=π/2-φ，与ε₃的夹角γ=ψ，所以有

cosα=sinψcosφ

cosβ=sinψsinφ

cosγ=cosψ

将上述三式的关系代入到式（8-30）中得ε_ψ、φ=sin²ψ（ε₁cos²φ+ε₂sin²φ-ε₃）+ε₃ （8-31）而平面应力状态下的物理方程为

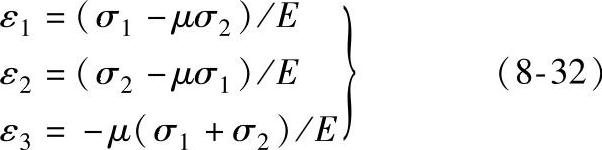
将式（8-32）代入式（8-31）得

ε_ψ、φ=[（1+μ）/E]sin²ψ（σ₁cos²φ+σ₂sin²φ）-μ（σ₁+σ₂）/E （8-33）

而平面上任意方向φ的应力（σ_φ）与主应力的关系有

σ_φ=σ₁cos²φ+σ₂sin²φ

代入式（8-33）得

ε_ψ、φ=[（1+μ）/E]sin²ψσ_φ-μ（σ₁+σ₂）/E （8-34）将式（8-29）代入式（8-34）整理后得

Δθ=-[（1+μ）/E]（1/cotθ₀）sin²ψσ_φ+（μ/E）（1/cotθ₀）（σ₁+σ₂）

由于在F射线测定时习惯用2θ角表示衍射角，所以上式改写为

Δ（2θ）=-[2（1+μ）/E]（1/cotθ₀）sin²ψ

σ_φ+（2μ/E）（1/cotθ₀）（σ₁+σ₂） （8-35）

在式（8-35）中，E为弹性模量，μ为泊松比，θ₀为无应力时的衍射角，ψ为衍射晶面（hkl）法线与物体表面法线的夹角，σ₁、σ₂为平面上的主应力，σ_φ为所需测定的应力。其中E、μ、θ₀为常数，ψ为人为设定的也已知，（σ₁+σ₂）为常数，所以式（8-34）中Δ（2θ）和σ_φ之间是线性关系。

2.常用的测定方法

（1）sin²ψ法。前已指出，式（8-34）给出了应变（Δ2θ）与欲测应力σ_φ的线性关系，但由于常数项中（σ₁+σ₂）是未知的，因此将式（8-24）两边对sin²ψ求偏导得

∂（Δ2θ）/∂（sin²ψ）-

[2（1+μ）/E]（1+cotθ₀）=σ_φ由于（Δ2θ）=2θ-2θ₀，代入式（8-35）经整理后得

σ_φ=-[E/2（1+μ）]cotθ₀∂（2θ）/∂（sin²ψ）

令 K₁=-E/2（1+μ） （8-36）

M=∂（2θ）/∂（sin²ψ） （8-37）这样前式就可改写为

σ_φ=K₁M （8-38）

式中的M即为2θ-sin²ψ关系曲线的斜率，而从式（8-35）可知，当确定了测点和应力方向后，σ_φ就有固定的数值，此时2θ和sin²ψ为直线关系，M为常数。所以在φ角固定的条件下，选不同的ψ角测定其对应的衍射角2θ，用最小二乘法可求出直线方程和斜率M值。从式（8-36）可知，K₁为一常数项，应力σ_φ决定于M，式（8-38）中的M相当于胡克定律中的应变，K₁即为弹性常数。对于sin²ψ法，式中的2θ角是由仪器给出的角度和衍射线强度数据，利用一定的定峰方法来确定。

（2）0°～45°法。在上述sin²ψ法中，为了用最小二乘法求出M，因此需设定多个ψ角（一般是四个）来测定对应的2θ角，这样测定时间大大加长。为了提高测试速度，可采用设定两个ψ角的方法。假定两个角为ψ₁和ψ₂，其中ψ₁＜ψ₂。对应测定的衍射角为2θ₁和2θ₂，代入式（8-35）则有

2θ₁=-[2（1+μ）/E]（1/cotθ₀）sin²ψ₁σ_φ+

（2μ/E）（1/cotθ₀）（σ₁+σ₂） （8-39）

Δ2θ₂=-[2（1+μ）/E]（1/cotθ₀）sin²ψ₁σ_φ+

（2μ/E）（1/cotθ₀）（σ₁+σ₂） （8-40）

将式（8-40）减式（8-39）得

σ_φ=[E/2（1+μ）]cotθ₀[1/（sin²ψ₂-

sin²ψ₁）]（Δ2θ₁-Δ2θ₂）

又因为Δ2θ₁=2θ₁-2θ₀，Δ2θ₂=2θ₂-2θ₀

所以有Δ2θ₁-Δ2θ₂=2θ₁-2θ₂

代入上式得

σ_φ=[E/2（1+μ）]cotθ₀[1/（sin²ψ₂-

sin²ψ₁）]（2θ₁-2θ₂）

设定ψ₁=0°，ψ₂=45°，且令

K₂=[E/2（1+μ）]cotθ₀[1/（sin²45°-sin²0°）]

=[E/2（1+μ）]cotθ₀（1/sin²45°）

则有σ_φ=K₂（2θ_0°-2θ_45°）=K₂Δ2θ （8-41）

这样在ψ角为0°和45°时测定衍射角2θ₀°和2θ_45°，再将其差值（2θ_0°-2θ_45°）乘以弹性常数K₂，即得到欲测应力σ_φ，显然这时的Δ2θ即相当于应变。

3.弹性常数K₁、K₂的确定 从K₁和K₂的公式看，它可以用弹性模量E和泊松比μ计算出来。但弹性力学中的E和μ是各向同性物体的物理常数，而金属晶体是各向异性的，其力学常数也是各向异性的，所以不能直接用E和μ的数值，因为它们是各个方向的统计平均值。K₁、K₂不能计算求得，一般都是用无应力试样对不同材料进行标定。试样通常为等强梁，这样根据等强梁尺寸和加载量可计算出主应力σ₁的大小和方向（等强梁主轴上）。然后在此方向上测定F射线衍射角。这时φ=0°，σ₂=0，σ_y=σ₁，ε_ψ.φ=ε_ψ，所以

ε_ψ=[（1+μ）/E]σ₁sin²ψ-（μ/E）σ₁ （8-42）

将上式对sin²ψ求偏导，然后再对σ₁求偏导，得

∂（∂ε_φ/∂sin²ψ）/2σ₁=（1+μ）/ε=S₂/2 （8-43）由于∂ε_φ/∂sin²ψ即为应变（ε_ψ）与sin²ψ关系曲线的斜率，所以

∂M/∂σ₁=S₂/2式中的M是在某个σ₁（此时是加载应力）之下，由所给定的多个ψ角的值，用最小二乘法求得的ε_ψ-sin²ψ曲线的斜率。然后改变加载负荷，使σ₁给定不同的数值，就得到不同的斜率M和ε_ψ-sin²ψ曲线（设曲线是直线），如图8-27所示；再用不同的多个M与σ₁值，通过最小二乘法求得M-σ₁曲线斜率S₂/2的值，如图8-28所示。

若令ψ=0°，则式（8-42）变为

（ε_ψ）_ψ=0=-（μ/E）σ₁ （8-44）

将上式对σ₁求偏导，得

（∂ε_ψ/∂σ₁）_ψ=0=-μ/E=S₁ （8-45）从图8-27求出各σ₁的（εψ）ψ=0，并作曲线（ε_ψ）_ψ=0-σ₁的斜率S₁（图8-29）。有了S₁和S₂/2，据式（8-42）和式（8-43）就不难求出弹性模量E和μ，此时的E和μ就是所测方向上的数值。

也可以采用下述办法先求μ，然后再求E。根据图8-27，不同的σ₁的曲线ε_ψ-sin²ψ汇交于一点A，在此点ε_ψ=0，并以不同的ψ角所对应的sin²ψ代入式（8-42），得

sin²ψ=μ/（1+μ）

从而有

sin²ψ=μ（1-sin²ψ）=μcos²ψ所以μ=tan²ψ （8-46）

然后由式（8-45），根据已求出的μ及已知S₁，即可求出对应的E值。

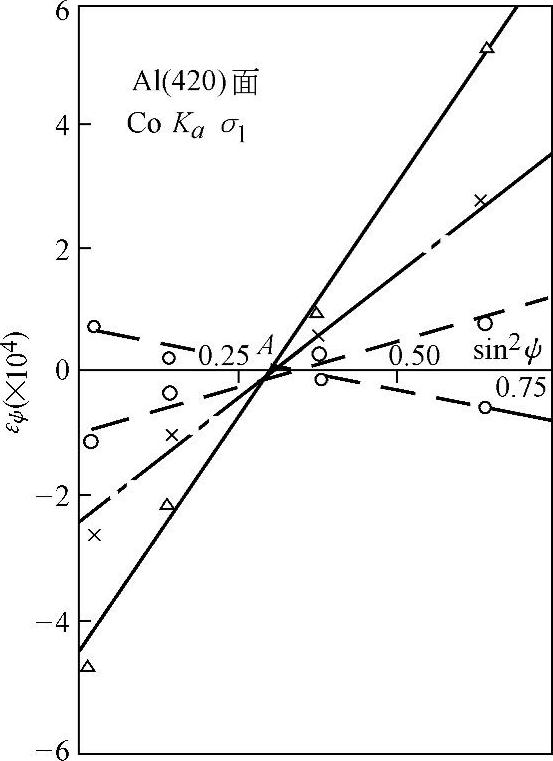
图8-27 ε_ψ-sin²ψ曲线

实际上在多晶体的晶粒之间还存在相间应力和相互影响（即第二类内应力），因此考虑S₂/2和S₁的值时，不可能像上述那样简单。这种影响对每个晶粒的应变和应力都将产生作用。据Hank的研究，对于钢材来说，对应力的影响占58.3%，对应变的影响占41.7%，所以α-Fe（211）面用CrK_α辐射时，得到：

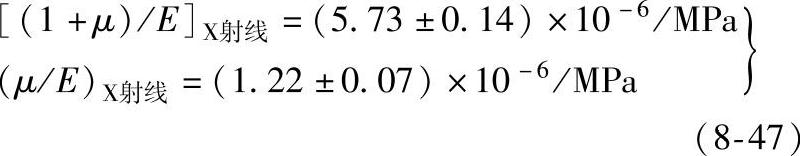
对于CoK_α，则α-Fe（310）面衍射有

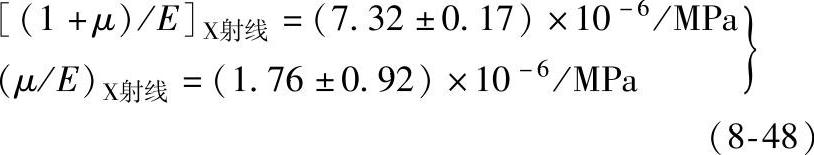
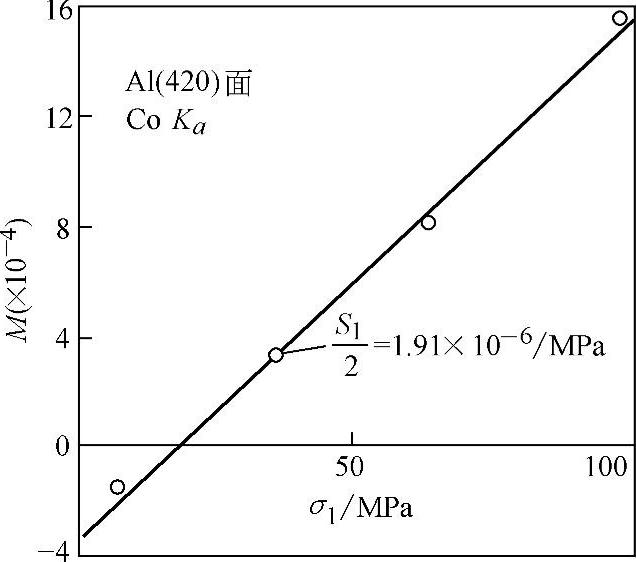
图8-28 M-σ₁曲线

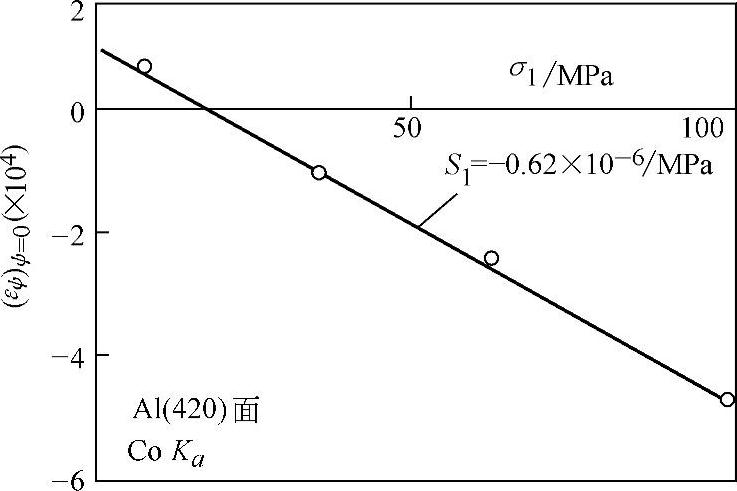
图8-29 （ε_ψ）_ψ=0-σ₁曲线

8.3.3.4 X射线应力测定装置

1.F射线应力测定仪简介 该仪器是以F射线衍射仪为基础，根据应力测定中工件体积大、需现场测试等特点进行改进而成的。它仍然是由F射线发生与控制部分和测角仪及支架组成，如图8-30a所示。现简要介绍如下。

（1）测角仪是仪器的主要组成部分，包括F射线管座、探测器（正比计数管、闪烁计数管、位敏探测器等）、2θ角的扫描弧形导轨及驱动装置、ψ角设置机构、发射和接收光栏（常用的结构为平行光束或准聚焦两种）。目前由于用特殊设计的超微型单窗口F光管，使仪器体积和重量均大大减轻，便于携至现场操作。

（2）支架分为两种，一种是三脚吸盘式（图8-30b），它可将测角仪吸附于大型工件的任一表面进行测定。当然在取下吸盘后用三脚支撑也可在实验室中对中、小工件进行测定。另一种为台车悬臂式或三脚悬臂式（图8-30c），它主要用来测定中、小型工件，有吸盘式支架后即可全部取代它。

（3）F射线发生和控制部分。F射线的发生仍由高压发生器和F光管组成。由于采用了高频振荡高压发生器，所以体积和重量也大大减轻，它已和高压控制、保护线路合并在一个组合屉中，以便携带。

（4）测试控制和数据处理部分。将常用的测试和数据处理程序编成专用软件，在Windows环境下利用微机将整个操作和数据处理自动化。所以只要将F射线对准了测试部位，然后在键盘上下达操作指令，测试过程即可全部自动进行。最后利用打印机将测试条件、测试结果的数据和曲线全部打印出来。

2.国内外生产的仪器简介 我国北京机电研究所从20世纪60年代引进该仪器，并开始自行设计制造我国的F射线应力测定仪。先后设计、生产了“FYL-72”、“FYL-73”、“FYL-74”及“FYL-75”型F射线应力测定仪，并将其中的73型和75型转产给邯郸无损探测仪器厂。目前上述产品均已淘汰，邯郸无损探测仪器厂又自行设计制造了BF-85型仪器。此仪器的特点为全面小型化、计算机化，从而成为真正的便携式微机控制的现代化仪器。其测试面积可小到ϕ1mm的区域，加附件还可测定残留奥氏体。

1994年以后邯郸市爱斯特研究所设计生产出了F-350型、F-350A型和F-350L型F射线应力仪。该仪器的最大特点是将过去国内外仪器以同倾法为主的设计结构改为以有倾角侧倾法为主。F射线入射光栅中心线与计数管中心线相向扫描，以它们夹角中心线来定ψ角的θ-θ法来完成测定操作。这样仪器的应用范围、测量精度都大大提高。该仪器不仅可直接测定铁素体、马氏体应力，还可直接测定奥氏体和部分有色金属的应力。它也可测定残留奥氏体量。

国内许多单位购置了日本理学电机株式会社和美国AMERHCAE STRESS TECHEOLOGHESHEC.以及爱派克国际有限公司的产品。这些进口仪器在结构上与国产仪器无大差异，主要是应用了位敏探测器，使每点的测试时间从几分钟缩短到了几秒钟。这不但节约了测试时间，而且也使仪器应用于生产线上成为可能。

8.3.3.5 X射线应力测定方法和数据处理

1.衍射角的测定

（1）抛物线近似法。理论上衍射线的强度分布是正态分布曲线，实际上不是标准的正态分布曲线。图8-31所示为衍射峰示意图。该图显示了通常的强度分布曲线。一般是以峰的顶端位置所对应的2θ角作为衍射角。如将峰高I_max的0.85以上部分近似作为抛物线，求出峰顶位置。

图8-30 国产X-350A、L型X射线应力测定仪

a）应力仪全貌 b）三脚吸盘式支架和θ-θ扫描ψ测角仪 c）立式台车悬臂式测量架

抛物线方程为y=Ax²+Bx+C，一次导数为y′=2Ax+B，显然当y′=0时为峰顶，所以2Ax+B=0，解此方程可得峰顶位置为x=-B/2A。现在y=I，x=2θ，代入就有

I=A（2θ）²+B（2θ）+C （8-49）

2θ_峰=-B/2A （8-50）

若从式（8-49）能求得方程系数A、B，则可从式（8-50）求得2θ_峰。确定A、B有三点抛物线法和多点抛物线法。

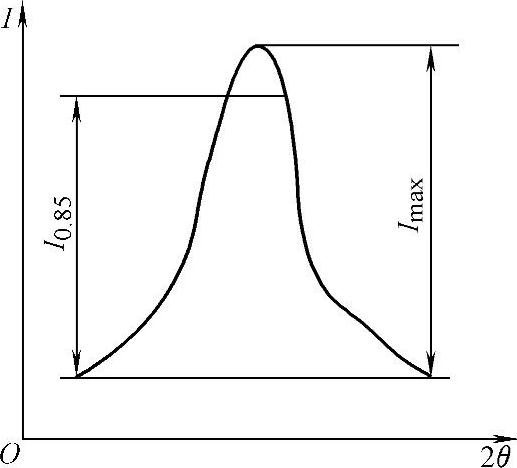
图8-31 衍射峰示意图

1）三点抛物线法。在峰顶附近等距离取三点2θ₁、2θ₂、2θ₃，从强度曲线上取三个角度对应的强度值（用探测器的脉冲计数表示）I₁、I₂、I₃，代入式（8-49）可得A、B、C值，再代入式（8-50）可求得2θ_峰。一般I₂在峰顶附近，所以I₂＞I₁、I₃。为了计算方便，用下述计算方法，令a=I₂-I₁，b=I₂-I₃，c=2θ₂-2θ₁=2θ₃-2θ₂（即c为三点的2θ步距）。代入式（8-49）经整理可得

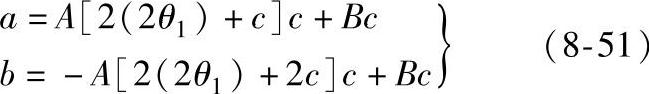
所以 a+b=-2Ac²

-2A=（a+b）/c²

B=-2A（2θ₁）+（3a+b）·2c代入式（8-50）得2θ_峰=2θ₁+[（3a+b）/（a+b）]（c/2） （8-52）

这样只要选定2θ₁和步距c，再测出I₁、I₂、I₃就可求得2θ_峰之值。

2）多点抛物线法。三点抛物线法对漫散峰（即峰宽很大，而峰背比较小的峰）将因峰顶难以确定，而造成定峰误差很大，所以通常衍射峰半高宽大于4°时即采用多点抛物线法。这时在漫散的峰顶附近取五点或七点的2θ_i值和强度I_i，运用最小二乘法求抛物线方程系数A、B，再代入式（8-50），求其峰值得

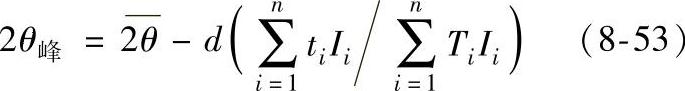
式中的n为取点数，2θ为所取各点2θ之算术平均值。当步距相等，点数n为奇数时2θ为各2θ_i之中值。而其他各项含义如下

d=0.4（n²-4）c

t_i=i-（n+1）/2（i=1，2，…，n）

T_i=12t²_i-n²+1（i=1，2，…，n）

I_i为各点之强度值。

（2）半高宽中点法。本方法将一个衍射峰的2θ_峰位置定义为半高宽中点的位置。在衍射峰高度的一半处作衍射峰背底的平行线，与峰的两腰交于2θ_低和2θ_高处，取差值β=2θ_高-2θ_低，此即为衍射峰的半高宽（图8-32），其中点位置即定义为峰顶位置2θ_峰。

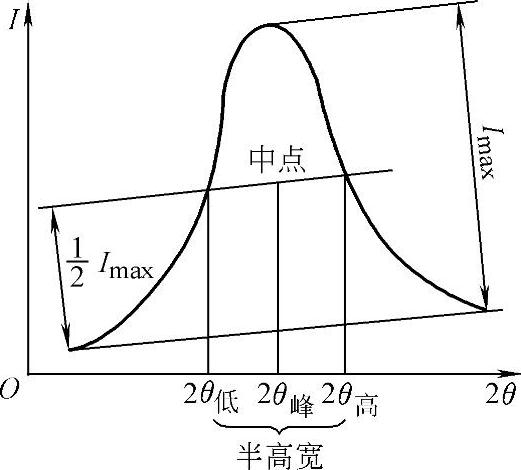
图8-32 半高宽定峰法

图8-33 半高宽中点定峰计算法

当在仪器作出的衍射峰曲线上（8-32）作图求得半高宽中点时，称为半高宽作图法。在用没有微机处理数据的旧型号仪器测定时常用此法定峰，它也是国家标准规定的定峰方法之一。也可用计算法求其半高宽峰值。按多点抛物线取点法取七点，如图8-33所示。在测得此七点对应的衍射强度I₁、I₂、…、I₇后，可按下式计算其2θ_峰值：

2θ_峰=1/2（2θ₂+2θ₆）+c/6{[3I_4-

2（I₁+I₂+I₃）/（I₃-I₁）]+[3I₄-

2（I₅+I₆+I₇）/（I₇-I₅）]} （8-54）式中，2θ₂和2θ₆为设定的已知值。

（3）各种方法测定的2θ角的标准偏差

1）抛物线法：

δ=0.4131[（n-1）/n（n+1）]^1/2c（n-1）/

式中 n——取点数目，如3、5、7、…；

c-各点间20步距：

I_峰——n个测定强度值中的最大值；

R-系数，R=0.85。

从式(8-55)可知，测量时I_峰值越大，测量偏差越小。所以实际测最时在保证足够峰背比的情况下尽量使I_峰计数值大一些，这样可减小测量的标准偏差。

2)半高宽中点计算法：

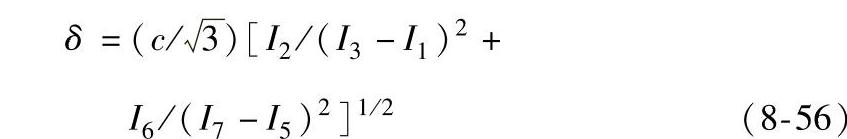
式中的I_i为各点之强度计数值。

2.弹性常数的实际测定F射线应力测定的弹性常数K₁、K₂是随材料、衍射面、入射线波长的选择不同而不同的。所以在实际测定时，对每一种未知K₁、K₂的材料都必须标定其数值，才能进行应力测定。目前列入国标的方法为等强梁法。用未知弹性常数的材料做成图8-34所示的等强梁，在其自由端加载荷P，梁的上、下表面的应力为

σ=Pl/（bh²/6） （8-57）

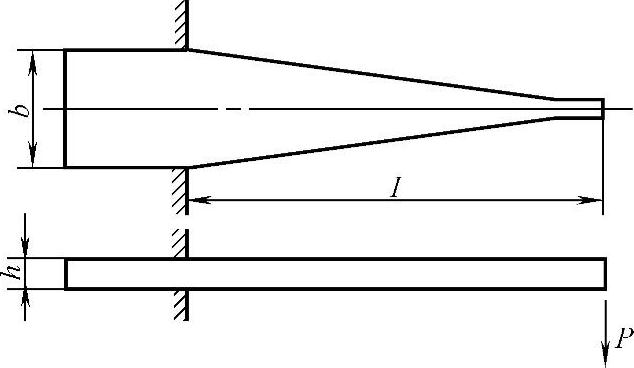
图8-34 等强梁尺寸

若梁满足l=bh²/6，据上式可知这时所加载荷P的数值和表面产生的应力数值相等。当然应力值有方向，上表面为正，下表面为负。这时用F射线应力仪在其上表面用sin²ψ法或0°～45°法分别测定2θ_i，求得其M或Δ2θ，由于σ=K₁M或σ=K₂（Δ2θ）两式中σ和M、Δ2θ已知，因而可求得相应的K₁、K₂值。为提高准确性，可采用多次加不同载荷以求其平均值。测定中必须注意的是：所加工的等强梁必须经去应力退火，经测定残余应力已近于零才能应用，否则在试验中残余应力会因加载而不断释放，将造成测量误差。而弹性常数为F射线应力测定的标准，所以测定K值时必须非常细心，用精度最好的仪器精心测定。

3.测定参数的选择

（1）靶材、衍射面和衍射角的选定。从弹性常数K₁、K₂的定义可知，它们均正比于cotθ₀（θ₀为无应力状态下所取材料衍射面的衍射角）。θ₀等于90°时cotθ₀为零，所以所选衍射面的θ₀应尽量趋近90°，从而使K₁、K₂数值也尽量小。在测定2θ时必然有误差，若弹性常数K值越小，则由2θ测定值误差引起的应力值误差就越小。据此原则对被测材料应先用F射线衍射卡片（PDF卡片）查出其所有能产生衍射的晶面间距d值，再据表8-1查得常用靶材（如Cr、Co、Cu等）的K_α、K_β、特征谱波长及相应的滤波片材料和最佳工作电压，最后用布拉格方程2dsinθ=nλ求出在上述各个特征波长下的衍射面。一般取衍射角2θ在150°～165°范围。由于仪器探测器扫描范围最大只能到170°左右，因此若衍射角太接近170°则可能使衍射峰不能完整出现，造成定峰困难。

表8-1 X射线靶材、特征谱波长、滤波片和工作电压

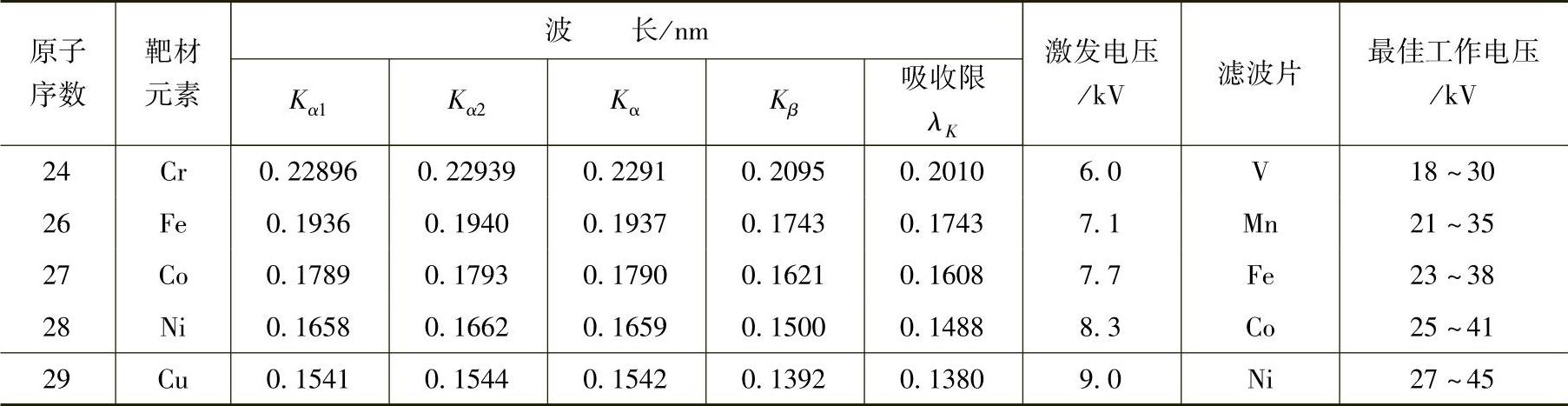
例如，当被测材料为碳钢、中低合金钢的α-Fe（马氏体、铁素体）时，通常参与衍射的晶面为（110）、（200）、（211）、（310），其相应的面间距为d₁₁₀=0.203nm，d₂₀₀=0.143nm，d₂₁₁=0.117nm，d₃₁₀=0.091nm。若用CrK_α和CoK_α来进行测试，其最佳衍射面分别为（211）和（310），CrK_α对（211）面的衍射角为2θ₀=156.4°，CoK_α对（310）面的衍射角为2θ₀=161.4°。CrK_α的滤波片为钒（V），最佳工作电压为18～30kV；CoK_α的滤波片为铁（Fe），最佳工作电压为23～38kV。

（2）其他参数的选择。

1）F射线管工作电流选择的依据，应在不超过发射管的规定功率的条件下，尽量使衍射线强度达到最大，但又不超过探测器的额定最大计数范围。

2）接收光栏张角的选定由衍射峰半高宽B来决定。当B≤5°时，用张角＜0.7°的平行光栏；若B＞5°时，用张角为0.90°～1.36°的准聚焦光栏。

3）探测器计数时间。在定时计数状态下一般应选择计数在10000～15000个脉冲的时间间隔内。

4）探测器扫描范围的确定是由峰形确定的。若是半高宽B＜4°的尖锐峰，用三点抛物线法定峰，其扫描范围只在峰顶附近的2°～3°范围内；若用半高宽或多点抛物线法定峰，则扫描范围需扩大一倍左右，即4°～6°。若峰形为B＞4°的漫散峰，则扫描范围必须将全部衍射峰做出来，其扫描范围可达到15°以上。

5）定点计数的步距一般采用0.5°/步，对于尖锐峰可小到0.2°/步，而对漫散峰可达到1°/步。

4.常用的测试方法为同倾法（习惯称常规法），即固定设置入射线与试样表面法线之间的夹角ψ₀，而不是固定设置衍射面法线与试样表面的夹角ψ（图8-35）。但国产的F-350型系列仪器则以固定设置ψ角的侧倾法为主。入射线与衍射线和衍射面的夹角为布拉格衍射角θ₀，它们和衍射面法线的夹角为它的余角η=90°-θ₀。从图8-35中可知：

ψ=ψ₀+η （8-58）

在用sin²ψ法测定时，是将ψ₀₁～ψ₀₄分别设定为0°、15°、30°、45°。据式（8-58）可知，ψ₁=0°+η，ψ₂=15°+η，ψ₃=30°+η，ψ₄=45°+η；用0°～45°法时设定ψ₀₁=0°，ψ₀₂=45°，则ψ₁=0°+η，ψ₂=45°+η。当有应力时，η=90°-θ，且θ≠θ₀。由于应变量不大，所以对应的Δθ/θ₀≈Δθ/θ，通常采用η=90°-θ₀的近似值。对于固定设置ψ₀法，虽然ψ角不同，但仍在同一直线上，所以斜率M不变，K₁也不变。但K₂就不同了，ψ₁=0°+η，ψ₂=45°+η。其计算公式如下：

K′₂=E/（1+μ）cotθ₀/[sin²（45°+η）-

sin²η] （8-59）

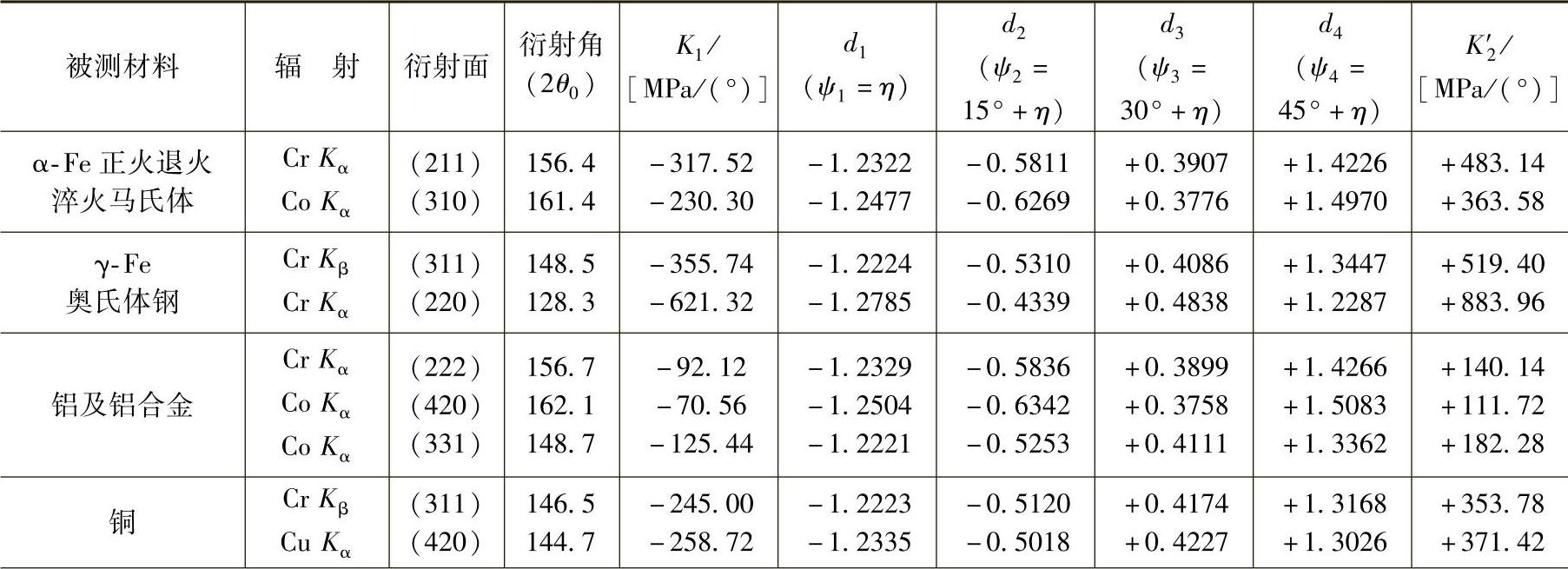
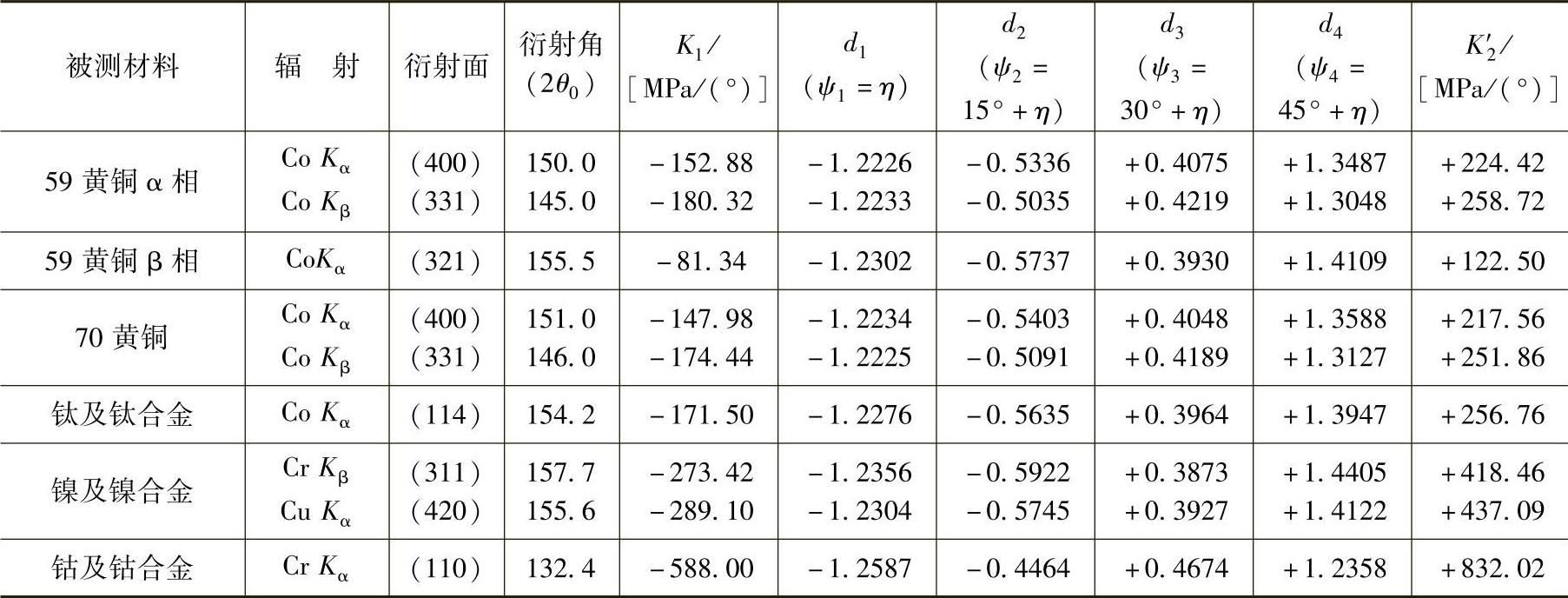
不同材料在不同入射线下的K₁和K₂′值列于表8-2中。(www.xing528.com)

5.数据处理

（1）定峰方法。我国国家标准GB/T 7704—2008

中规定可用的定峰方法为半高宽法和抛物线法。

（2）求应力值。在sin²ψ法中，求M值用最小二乘法，经整理后其计算公式如下：

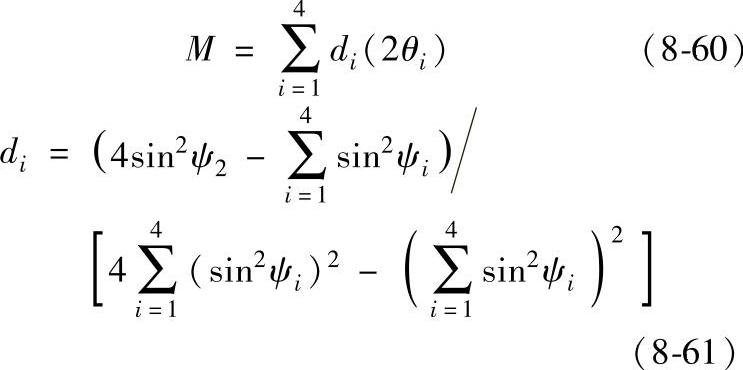
在表8-2中已将不同被测材料在各种测试条件下的d_i值计算出来了，因此测试者可直接将其数值代入式（8-60）中求M值。

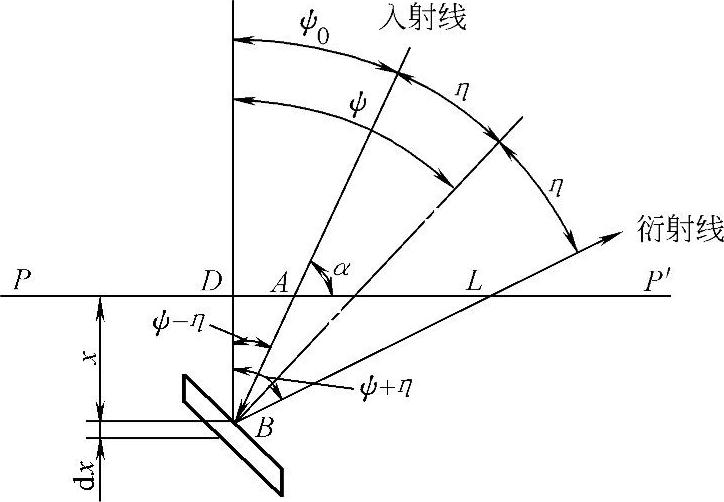
图8-35 应力测定时的衍射几何图

表8-2 常用材料的测定参数和弹性常数

（续）

（3）测量误差的计算。

1）衍射角的标准偏差。每次2θ角测量后的标准偏差δ按式（8-55）、式（8-56）计算。

2）应力值的标准偏差和可信度：

①0°～45°法由于只测定两点，所以两点的误差对应力值误差的贡献各占50%，其标准偏差为

σ_s=K（δ²₀°+δ²₄₅°）^1/2 （8-62）式中的K=K₂（固定设置ψ法）或K′₂（固定设置ψ₀法）。

②sin²ψ法中2θ_i的四个值的标准偏差δ_i在应力值的标准偏差中各以其对应的d_i值为权重来起作用，所以其计算公式为

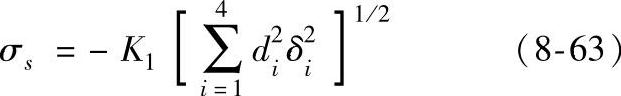
③可信度的计算。标准偏差为测定时的最大偏差，而实测偏差分布在真值σ的±σ_s的领域内，成正态分布。取真值左右的1/2面积内对应的测点为可信度Δσ，则有

Δσ=±0.6745σ_s （8-64）

6.对测点表面的要求和处理F射线测定的是表面应力，因此测点表面状态对测量影响极大。测量时要求表面无锈迹、油污，若为加工面则必须是精加工面。若测点表面不合格，则必须用砂轮、砂纸打磨，然后再用电解抛光将打磨层去除（否则有打磨附加应力），并降低其表面粗糙度。

8.3.3.6 X射线应力测定中的强度校正

1.F射线晶体衍射线强度的空间分布F射线晶体衍射线强度的空间分布是不均匀的，是随衍射角2θ而变化的。其规律为2θ在90°处最弱，而越趋近0°和180°则越强，其结果就造成衍射峰背底倾斜，由于是高角背底抬高，所以使峰顶位置向高角偏移。在应力测定时是以不同的ψ或ψ₀角入射的，这时随ψ、ψ₀角的增大，背底倾斜则更加严重，这样由于这种差异使2θ角测量值产生系统误差。所以必须找出其中的衍射线强度变化规律，将这种系统误差消除。实测证明，这种误差在0～700MPa的试样上可造成40～100MPa的系统误差。

2.强度校正的计算方法 据有关资料证实，强度校正的计算公式为

I_校=I_测[（1+cos²2θ）/sin2θsinθ]sin（ψ+θ）×（1-tanψcotθ） （8-65）

或者为

I_校=I_测[（1+cos²2θ）/sin2θsinθ]×

cos（ψ₀-2θ）/[cos（ψ₀-2θ）-cosψ₀] （8-66）

式（8-65）为固定设置ψ法的公式，式（8-66）为固定设置ψ₀法的公式。式中I_测为定点计数时的某点衍射线强度计数，2θ、θ即为此点对应的衍射角，ψ或ψ₀是由仪器设定的。

在最新设计的国产仪器中，这种校正计算已固化在计算程序中。

8.3.3.7 大晶粒材料的残余应力测定

1.材料晶粒粗大对衍射峰的影响 当测试对象是经过加热、铸造、焊接等热加工的工件，往往会出现晶粒粗大的现象，即晶粒的平均尺寸大于30μm，而对于一些有色金属材料往往晶粒会更粗大。这时在不同ψ或ψ₀角下测定的衍射峰将会出现极大的畸变，主要是大大偏离正常的强度分布规律，即原来强度大的峰会大大减弱，而弱的峰会大大增强。这种现象的出现会使2θ的测定值产生极大误差，而且是无规律的、分散度极大的误差，所以应设法尽力消除这种误差。目前采取的办法就是摇摆法，即在测试时，使入射F射线在设定的ψ或ψ₀角附近作±2°～±12°的摇摆，使参与的衍射面数增加，从而大大恢复衍射线强度分布的规律。

2.校正系数和应力计算 要求得校正系数，必须先求得摇摆中因ψ±Δψ而形成的2θ的统计平均值，据资料介绍，其公式为

2θ=[2（1+μ）/E]（1/cotθ₀）K′₁σ_φ+

（2μ/E）（1/cotθ₀）（σ₁+σ₂） （8-67）

式中K′₁=（F/4-Δψ+tanηlnD-tanηG）/（2Δψ-tanηlnD）

D=cos（ψ-Δψ）/cos（ψ+Δψ）

F=sin2（ψ+Δψ）-sin（ψ+Δψ）

G=[cos²（ψ-Δψ）-cos²（ψ+Δψ）]/2将式（8-67）对K′₁求偏导：

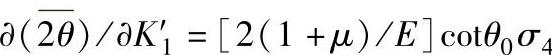
令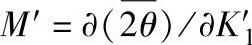，而sin²ψ法中的K₁=（E/2）（1+μ）cotθ₀所以，所测应力σφ有

σ_φ=K₁M′ （8-68）

此即为摇摆法测应力的公式。K₁是已知弹性常数，关键是如何求得M′。对于一些常用材料（如α-Fe、γ-Fe和Al）分别采用CrK_α（211）面、CrK_β（310）面和CrK_α（222）面测试时，在不同±Δψ值下的K₁′值列于表8-3中，有了K′₁值，再将测定的2θ值与K′₁对应，用最小二乘法求2θ-K′₁直线的斜率即为M′，然后再代入式（8-68）即可求得应力值。

对于0°～45°法，式（8-68）变为

式中的K′₂与K′₁有关，经计算后其数值列于下面的表8-4中。

在国产BF-85和F-350仪器中，均带有摇摆法程序，但只能测出2θ，而计算还需用本手册表8-3和表8-4求得K′₁和K′₂，再用最小二乘法求M′，最后依据式（8-68）、式（8-69）求得应力。

表8-3 不同材料试样、不同辐射的K′₁值

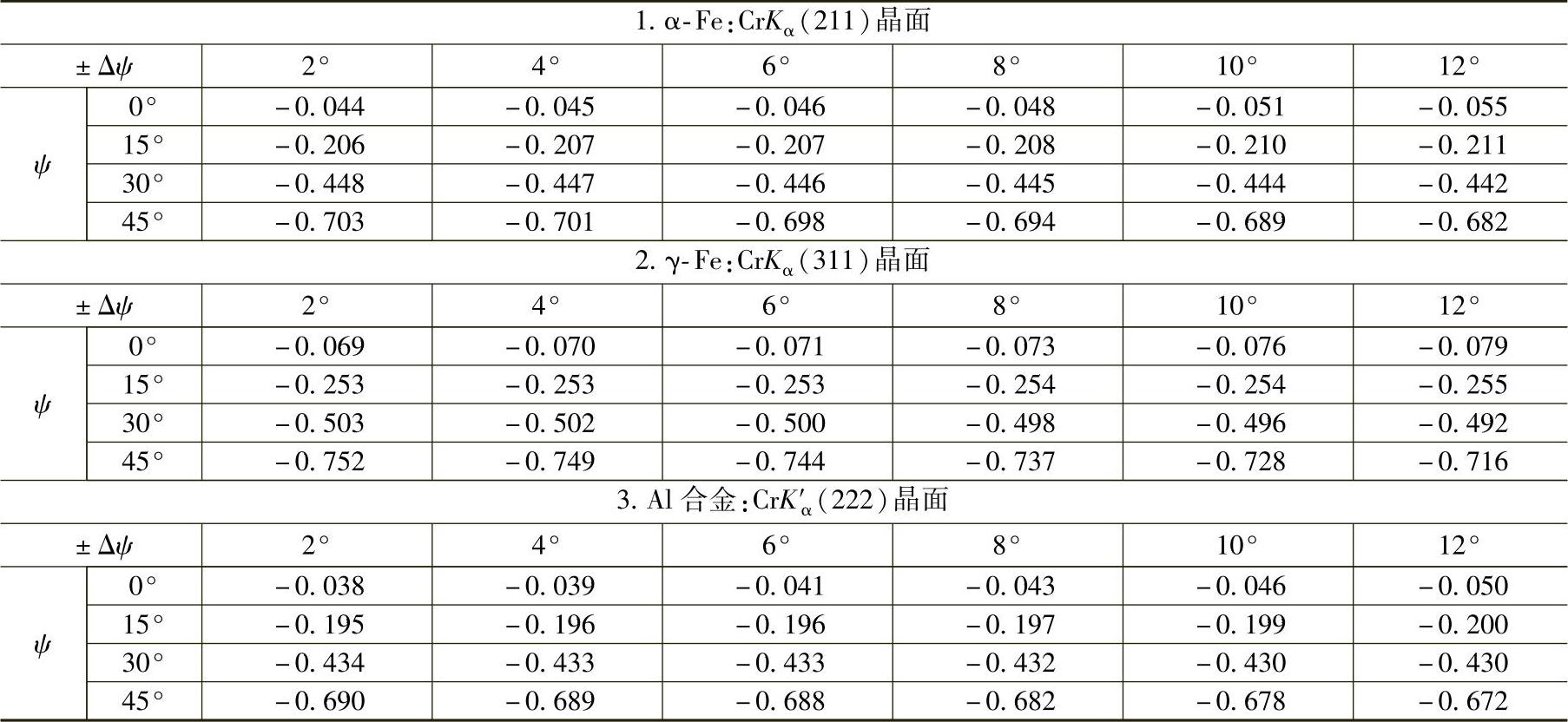
表8-4 不同材料试样、不同辐射的K′₂值 [单位：MPa/（°）]

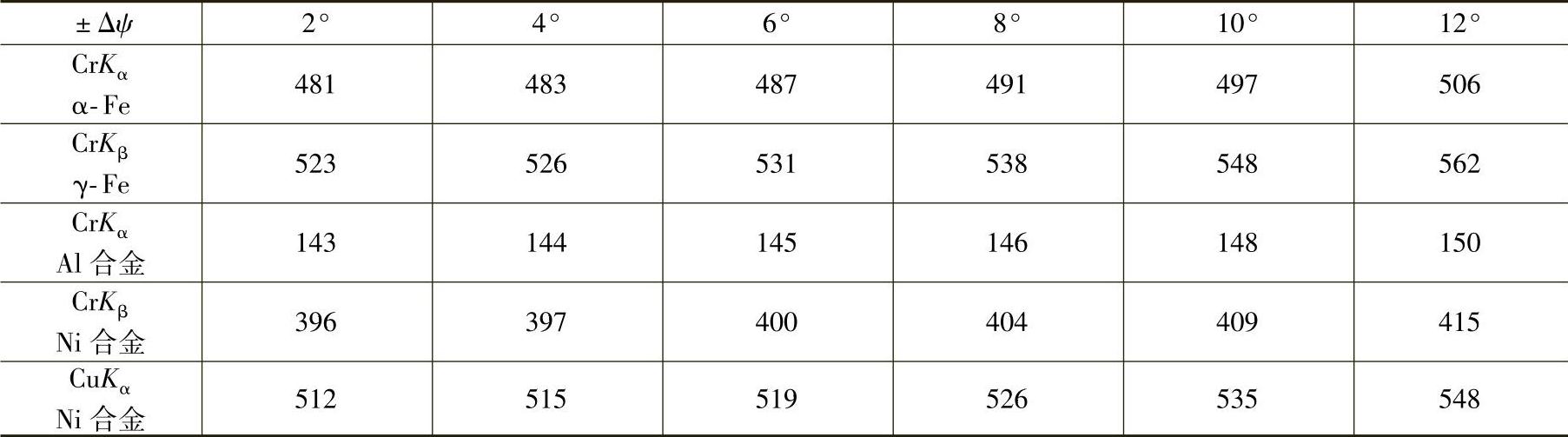
8.3.3.8 织构材料残余应力的测定

1.材料织构对应力测定的影响 它和前述大晶粒的影响相似，也会因晶粒取向一致（形成织构）而产生不同ψ角入射时衍射峰强度出现不正常起伏现象（或称异常现象），并由此使2θ-sin²ψ曲线的非线性更为严重，使应力测定无法进行。织构材料晶粒并不粗大，而是绝大多数晶粒空间取向一致，使材料近于单晶体，有了各向异性，也使摇摆法无法改善衍射线的强度异常。这就导致了织构材料独特的测试方法（织构不严重的材料仍可用摇摆法测定）。

2.测定方法

（1）H晶面法。对于立方晶体，即使是单晶体，其{hhh}和{hoo}两个晶面族具有衍射线强度以及2θ-sin²ψ曲线的线性不受其各向异性的影响，仍保持正常的强度分布和2θ-sin²ψ的线性关系。这一类晶面有（100）、（111）、（200）、（222）等，我们统称这类晶面为H晶面。当然测定时必须先测该材料所用H晶面的F射线应力测定弹性常数K₁、K′₂等。

（2）高指数晶面法。这类晶面由于其重复性因子大，因此其衍射线强度的异常被减弱，并且其2θ-sin²ψ曲线的线性关系非常好，能满足应力测定的需要。所以在用H晶面法有困难时也可用此方法来测定。这类晶面在α-Fe中如（732）（651）、（721）（633）（552）、（710）（550）（543）晶面族。当然它也有一个弹性常数问题。常用材料有织构时常用的衍射面和衍射角见表8-5。

表8-5 常用材料有织构时常用的衍射面和衍射角

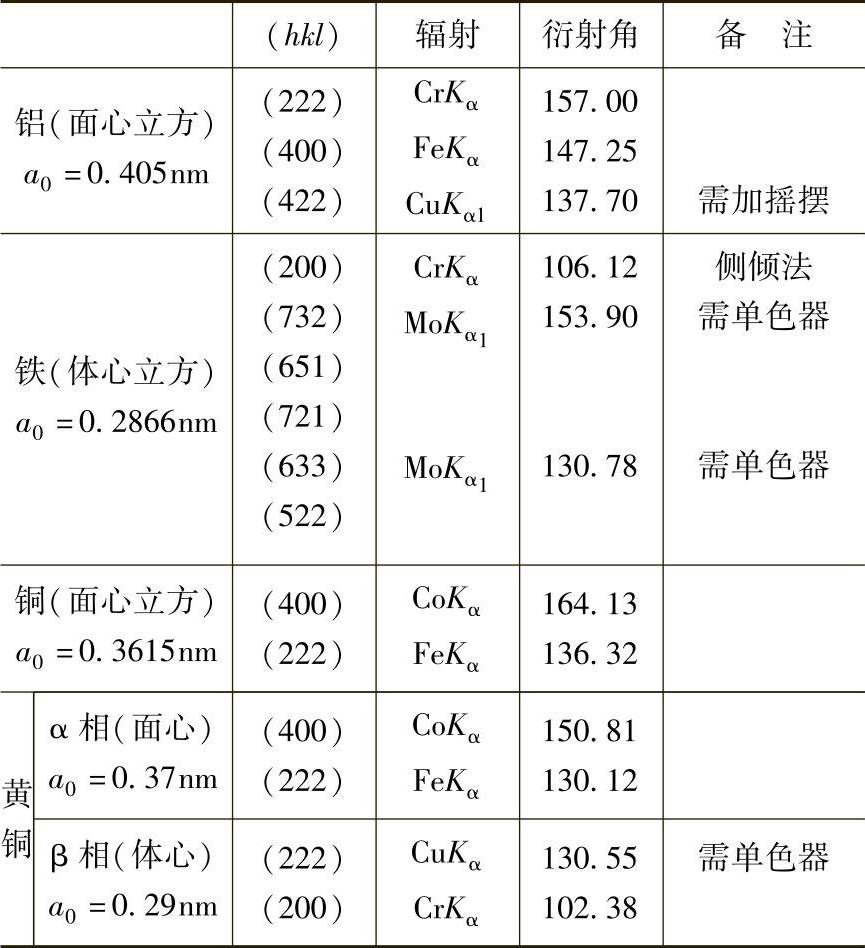
从上可知，其衍射面的衍射角往往较小，已在一般应力测定仪探测器扫描范围（140°～170°）之外，所以往往织构材料应力测定只能在F射线衍射仪上进行。

8.3.3.9 复杂形状工件的残余应力测定

前述的F射线应力测定中将欲测表面定义为平表面，而实际工件的欲测表面往往是曲面。轴、杆、齿轮等工件的表面，可以是凸圆柱面，也可能是凹圆柱面，因此根据不同情况测定的方法和应力计算方法均需有所改变。

1.凸圆柱形弧面切向应力的测定

（1）圆柱形弧面的ψ角是在设置角两侧一定范围内不均匀分布的，它随试样直径大小、光斑照射面积宽度而变化，而两侧扩展角度的范围不对称。此外，设置的ψ₀角是在圆弧顶点（图8-36），而顶点两侧吸收射线的差异也远大于平面摇摆法。因此必须先求得不同条件（试样直径、照射宽度）下ψ₀角的统计平均的上、下限ψ₀₁、ψ₀₂和这时的吸收规律，再进行校正。

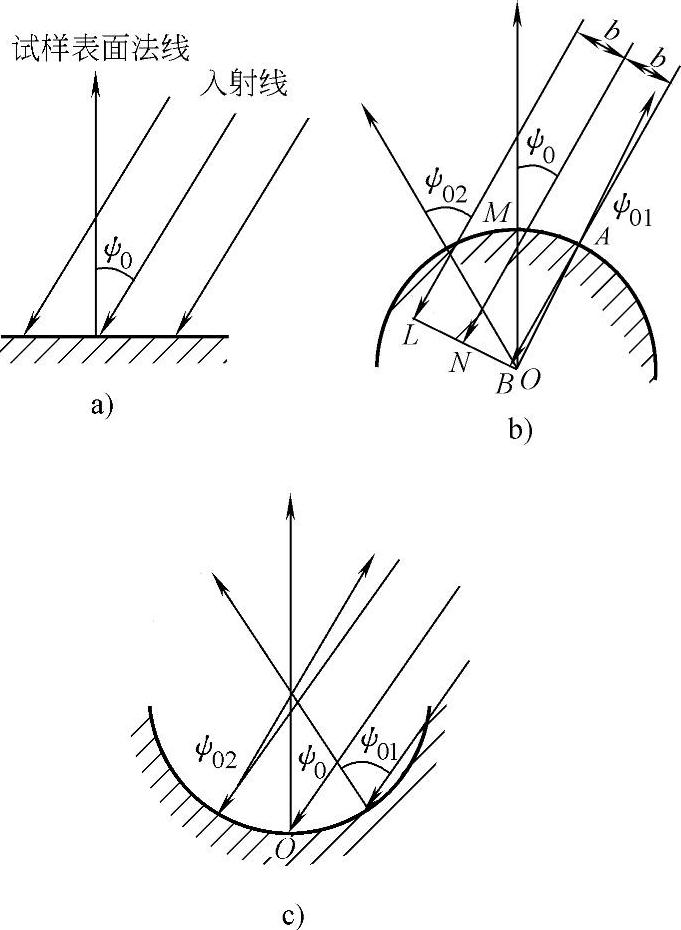
图8-36 平板和圆柱试样切向应力测定时的几何关系

a）平板试样 b）、c）圆柱试样

（2）计算公式。圆柱弧面测定2θ角是统计平均值，当入射线相对圆柱顶点端母线入射角为ψ₀时测得的衍射角为

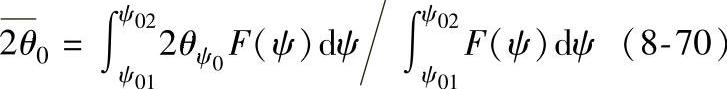
式中的积分区间[ψ₀₁，ψ₀₂]应该是ψ₀、B（照射面积宽度）及D（试样直径）的函数。依图8-36b经推导可得到积分区间上、下限与ψ₀、B和D的关系：

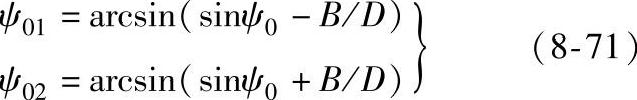
式（8-70）中的F（ψ）与不同ψ₀角（或ψ角）下光程Rcosψ₀及吸收系数有关，经推导得

F（ψ）=（1-tanψtanη）cos（ψ-η）（8-72）将其代入式（8-71），且据ψ=ψ₀+η，将积分限取为ψ₁和ψ₂，则2θ的统计平均值为

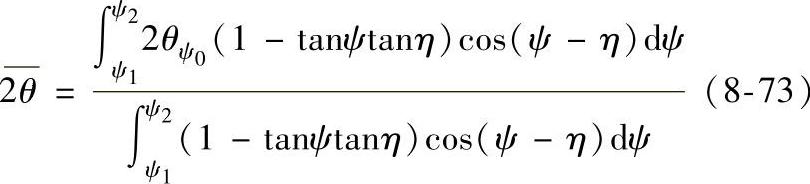
将其代入sin²ψ法的应力公式中，得

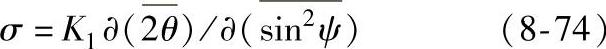
其中

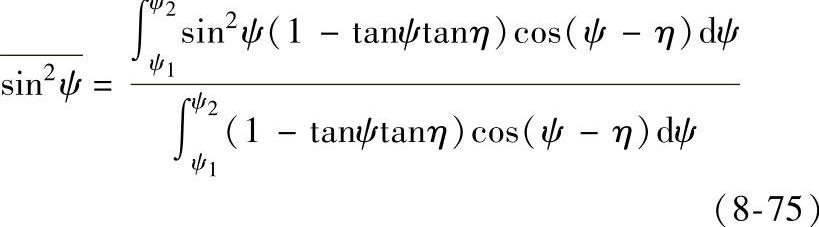
对应于0°～45°法则，有

其中

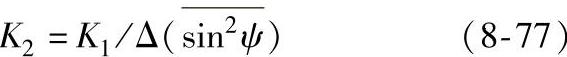
所以先据式（8-75）求出对应于各个设置的ψ₀角（或ψ角），求出对应的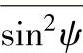的数值，这样就可用式（8-74）和式（8-76）求得应力值。（3）计算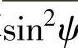时，首先需确定对应ψ₀=45°的上限ψ_02max。从图8-36b可知，过A点的衍射线若与A点处柱面相切，则得到衍射线从试样射出的最大极限角（角度再增大，则衍射线将被试样遮掉一部分），且有ψ_02max=90°-2η，代入式（8-71）得

sinψ₀+B/D=sin（90°-2η）

B/D=sin（90°-2η）-sin45°（8-78）由此可知，当被测材料和辐射选定后，η角就确定，若试样直径D为已知，即可计算出允许的极限照射宽度（即入射光栏的窗口宽度）。再据各测试方法中的ψ₀（或ψ角）的数值，用式（8-71）求得其上下限ψ₀₂、ψ₀₁（或ψ₂、ψ₁），这样即可得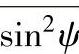值。而2θ即为仪器的测定值，用式（8-74）、式（8-76）即可求得所测应力值。

（4）不同材料测定的最小直径。从上述内容可知，测定值的校正和照射面积宽度B有关。目前一般测试常用宽度为2～8mm，最小可到0.5～1.0mm。从测量的精度及重复性考虑，希望B越大越好，因为这样计数率高，精度也就高，但从工件应力分析出发则希望测点面积越小越好。如圆柱试样，D越小则希望B也越小。经计算，将不同材料在不同辐射条件下，不同B值对应的最小直径D值列于表8-6。

表8-6 不同材料、不同辐射面和不同光栏狭缝宽度下的最小可测直径 （单位：mm）

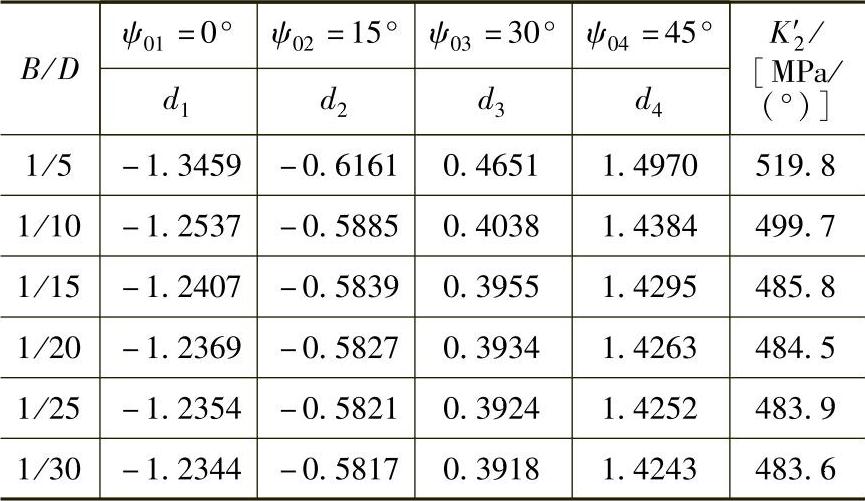
对于α-Fe及一般钢材用CrK_α对（211）面衍射的sin²ψ的d_i值和0°～45°法（均为固定设置ψ₀法）的K′₂，在不同B/D情况下的数值见表8-7。

表8-7 α-Fe，（211）面，在CrK_α辐射条件下不同B/D值的d_i和K′₂值

2.圆柱形弧面轴向应力测定 测定时的几何关系如图8-37所示。在照射面积内，除圆弧顶点处的入射线和ψ角设置平面、探测器扫描平面皆在与试样表面垂直的平面内以外，其他的入射线及上述两平面皆与表面法线有一夹角γ，而且在照射宽度B（B=2b）内，各点的夹角γ_i均不相同。但这时由于ψ设置面与顶点法线Oz平行，所以γ角分布是以顶点为中心相对Oz对称分布的。照射面积为S=Bl=2bl。若将照射面积取面积单元ΔS=dyl，则随dy位置变化，该面积单元对应的γ_i角不同。实际测得的2θ值应是±γ_max区间内的统计平均值2θ，由于照射面积长度l为常量，所以积分区间变化为-b到+b之间，其统计平均值为

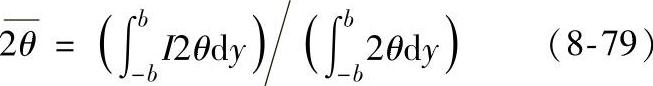
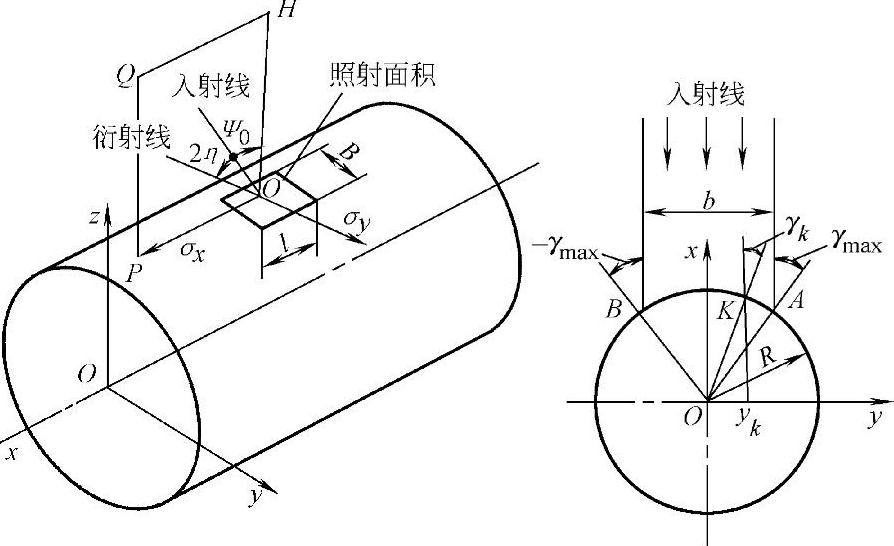
图8-37 凸圆柱面轴向应力测量的几何关系

将各点的几何关系式代入，得

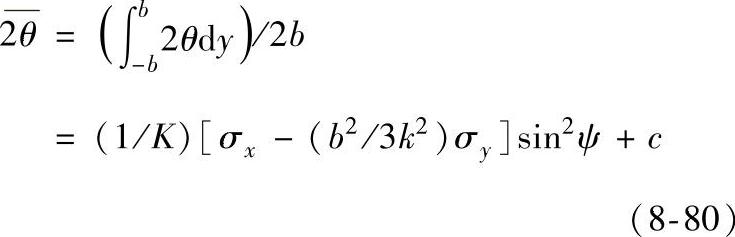
式中的σ_y为用式（8-21）测定的切向应力。这时用测得的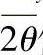值和设置的ψ角求得应力值为

σ′_x=K₁（∂2θ/∂sin²ψ）=σ_x-（b²/3R²）σ_y所以σ_x=σ′_x+（b²/3R²）σ_y=σ′_x+（B²/3D²）σ_y （8-81）

式中的R为试样半径，σ′_x为用仪器测出的值不加校正的应力值，所以（B²/3D²）σ_y即为校正项Δσ_x。不同B/D对应的B²/3D²值见表8-8。

表8-8 不同B/D对应的B²/3D²值

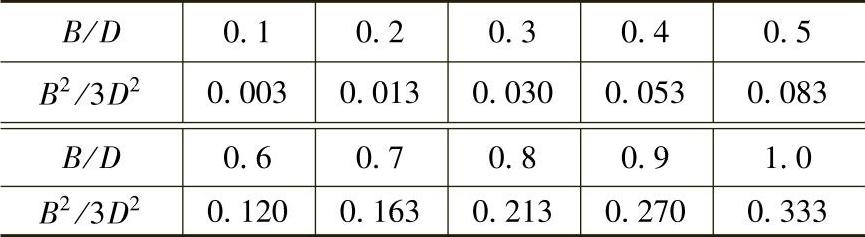
从计算可知，若切向应力σ_y＜50MPa，则即使B=D，轴向应力的校正值也只有16MPa，而这时若测出的未校正轴向应力在160MPa以上，则不加校正其应力值相对误差也小于10%。

3.侧倾法及其应用 上述应用的探测器扫描平面与ψ角（或ψ₀角）设置平面重合的测试方法称为同倾法，在以前所述各种测试中它已被很好地应用。但是当欲测凹面试样，如凹圆柱面以及类似的工件表面时，同倾法因探测器扫描位置受限制而无法应用。因此出现了将探测器扫描平面转90°进行测试的侧倾法，其几何关系如图8-38所示。这是一种标准的侧倾法，它固定设置的是衍射晶面法线与试样表面法线的夹角ψ，而且它的衍射几何关系和F射线衍射仪一样，在试样不动的情况下它是由F射线和探测器两者相向扫描来实现的。这种设置大大减少了吸收对衍射线强度不均匀的影响，从而大大提高了测量精度。它不仅适用于凹面试样，在其他各种测试中也有很多优点，国产F-350型仪器系列就是完全按此来设计的。早期的仪器都按同倾法设计。这种仪器是按固定设置ψ₀角的原理，加上侧倾工作台使其实现侧倾法，所以也是一种无倾角的侧倾法。其几何关系如图8-39所示。这种方法的影响因素多，关系复杂，测试精度也不如有倾角侧倾法高。但因我国尚在大量使用这样的仪器，所以也有必要介绍一下其测试方法。

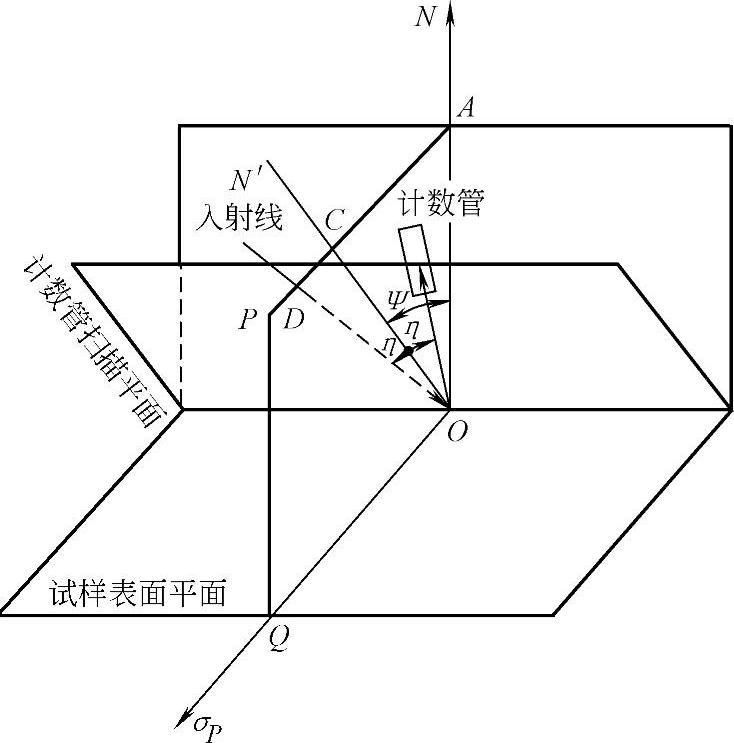
图8-38 有倾角侧倾法中的几何关系

（1）有倾角侧倾法计算公式及测试方法。

1）计算公式。sin²ψ法：即用前述的式（8-38）来计算。

σ_φ=K₁M

设定四个ψ值，测出2θ，然后求出2θ-sin²ψ曲线的斜率M，即可求出应力值。

图8-39 无倾角侧倾法中的几何关系

0°～45°法：即用前述的式（8-41）来计算。

σ_φ=K₂Δ2θ

在ψ分别为0°和45°处测出2θ值，代入上式即可求得应力值。注意此时用的弹性常数是K₂，而不是K′₂。

2）测试方法。用侧倾法在凹面试样上测试时设置ψ角上限以45°为宜，这时4个ψ角即为常用的0°、15°、30°、45°，求斜率M的最小二乘系数的d_i值见表8-2。若对平面试样，其ψ角设置上限可达56°，所以4个角度值可为0°、24°、40°、56°，其d_i值见表8-9。

（2）无倾角侧倾法。

1）计算公式。从图8-39可知，它测定的应变ε_αβ为

ε_αβ=asin²ψ₀+bsinψ₀+c （8-82）其中，a≈（1/K₁）cos²η₀σ_x，b≈（-1/K₁）cosη₀τ_xy，而c为常量，由此可得

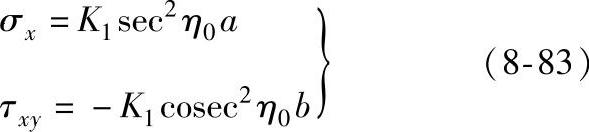
在不同ψ₀角测2θ值，用式（8-82）得ε_αβ的方程式。用多个ψ₀角的测量数据，再用最小二乘法求得a、b值，公式如下：

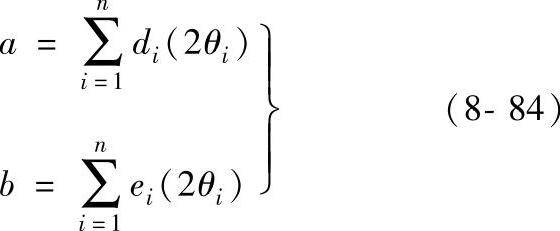
代入式（8-83），即可求得正应力σ_x和切应力τ_xy。

2）测试方法。常用下述两种方法：

①±ψ_0i直线法。由于切应力τ_xy的存在，在设置ψ_0i时，若只设置+ψ_0i（0°、15°、30°、45°）将产生极大系统误差。若采用正负对称设置则可消除此误差。因为同一对±ψ₀角测定时，其对应的sinψ₀项数值相等符号相反，即

2θ_+ψ0i=a（sin²ψ_i）+bsinψ_i+c所以2θ_-ψ0i=a（sin²ψ_i）-bsinψ_i+c

（2θ_+ψ0i+2θ_-ψ0i）/2=asin²ψ_0i+c （8-85）

（2θ_+ψ0i-2θ_-ψ0i）/2=bsinψ_0i （8-86）即（2θ_+ψ0i+2θ_-ψ0i）与sin²ψ_0i成正比，（2θ_+ψ0i-2θ-ψ_0i）与sinψ_0i成正比，其系数分别为a和b，用（8-84）和表8-9中的d_i（对于α-FeCrK_α）可求得。

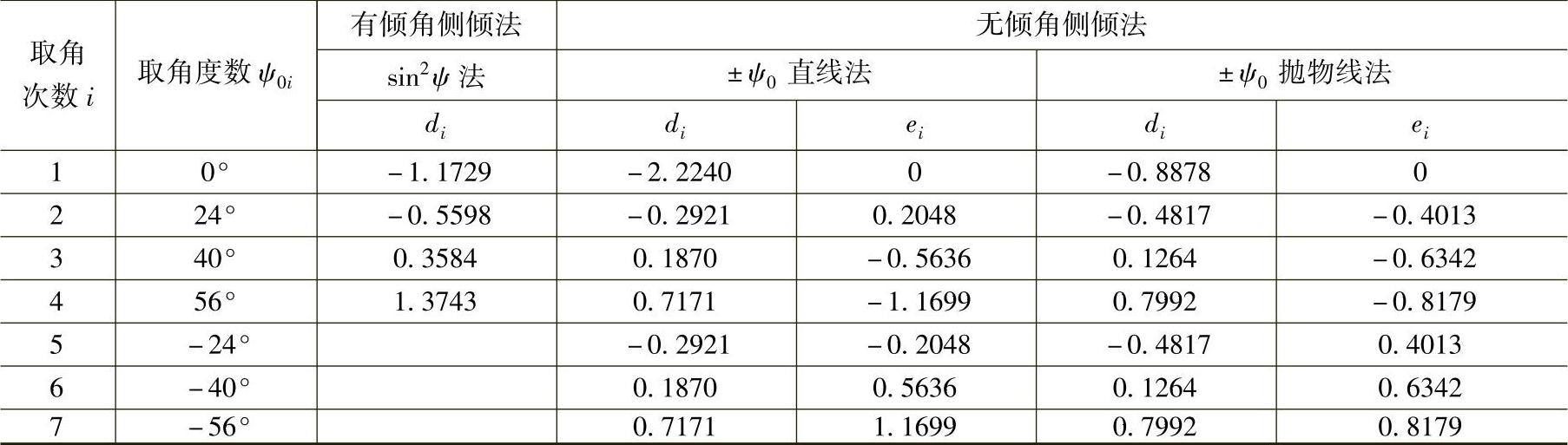
②±ψ_0i抛物线法。若不用Δ2θ_i，而直接用2θ_i时，它和sinψ_i成抛物线关系，用表8-9中的d_i、e_i值可求出方程式中的系数，从而求出应力。在表8-9中，ψ_0i角选用0°、±24°、±40°、±56°的原因是：一方面这时可测试到ψ=56°以上的衍射线；另一方面同倾法设置的0°、15°、30°、45°是ψ₀角，其对应的ψ角为ψ₀+η，对α-Fe（211）面、CrK_α时其η≈11.8°，所以其ψ角为0°、26.8°、41.8°、56.8°，因此，在侧倾法设置ψ角时为与同倾法的ψ₀角设置相近而选用了上述的角度。注意在无倾角侧倾法测定时，若仍用0°、24°、40°、56°设置ψ角，则其K₁值将需调整，经计算其数值为K₁=-347.1MPa/°。而d_i、e_i值见表8-9。

表8-9 α-Fe、（211）面、CrK_α测定时的ψ_0i、d_i、e_i值

4.典型复杂形状零件的测定

（1）曲轴圆角残余应力的测定。所谓曲轴圆角是指轴颈与轴柄的过渡圆角。轴颈表面高频感应淬火后，圆角区因处于过渡区，会产生残余拉应力峰。曲轴运行中圆角区的工作状态是承受拉压、弯曲、扭转的复杂交变应力，存在于表面的拉伸残余应力将使曲轴疲劳寿命大大降低。因此轴颈淬火后，其圆角部位也需予以强化（高频感应加热圆角淬火或圆角滚压）。测定圆角部位应力难度较大，可采用图8-40所示方法，图8-40a为圆角位置，图8-40b为测定时ψ₀角的设置，图8-40c为测点部的双曲圆拱。一般轴颈半径是圆角半径的10倍以上，所以在测点尺度小于10mm的范围内，可将圆角近似看成是凹圆柱面。此处建议用有倾角侧倾法，可以保证从0°～45°的ψ角设置，而且几乎不存在吸收因子的影响，如图8-40b所示。由于是凹圆柱面，所以所测数据还需用照射面积宽度B与圆角直径D之比来进行校正（表8-7，表8-8），按圆角半径确定照射宽度可参照表8-6。

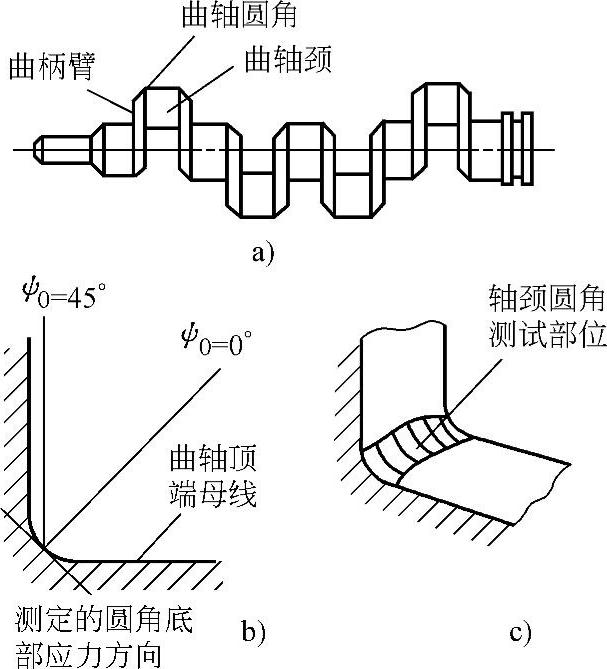
图8-40 曲轴圆角应力测定示意图

（2）齿轮根部残余应力的测定。

1）轴向应力的测定。齿轮根部可看成是半径很小的凹圆柱面，所以首先必须使照射宽度（即入射光栏狭缝宽度）B小于圆柱面直径，其值往往小于1mm，因此为了增强衍射线强度，应尽可能增加照射面的长度。测定数值需用表8-8的B²/3D²的数值进行修正。

2）切向应力的测定。由于相邻两齿对ψ角的设置产生极大阻碍，因此测试困难。一种方法是用侧倾法中±ψ_0i法，在可能的范围内设置正负ψ_0i值，应用计算的d_i、e_i值，求出系数a、b值后可求得切向应力。与轴向应力相同，此时的测定值也要进行圆柱面测定时的校正。另一测试办法是先测定其轴向应力，然后在经相同热处理的齿轮表面（表面淬火）或齿轮端面（渗碳淬火）上测定某点的任意相互垂直的两个正应力σ_x和σ_y，再求得其零应力下的sin²ψ_Δ2θ=0，从而求得切向应力σ_τ。

据前述可知：

Δ2θ=-[2（1+μ）/E]（1/cotθ₀）sin²ψ·

σ+（2μ/E）（1/cotθ₀）·（σ₁+σ₂）现取σ_φ=σ_x，且有σ₁+σ₂=σ_x+σ_y，应变时Δ2θ=0代入上式，经整理有

sin²ψ_Δ2θ=0=[μ/（1+μ）]（1+σ_y/σ_x） （8-87）只要在非齿根的平面上测得任意的相互垂直的σ_x、σ_y值代入式（8-87），即可求得sin²ψ_Δ2θ=0值。这时式（8-87）变为

σ_y=[（1+μ）/μ]sin²ψ_Δ2θ=0σ_x令σ_x=σ_z（轴向应力），则σ_y就是切向应力σ_t，所以上式变为

σ_t=[（1+μ）/μ]sin²ψ_Δ2θ=0σ_z （8-88）将测得的σ_z值和式（8-87）算出的sin²ψ_Δ2θ=0值代入式（8-88）即可求得切向应力σ_t。

8.3.3.10 残余应力沿层深分布的测定

测定沿层深分布的残余应力，目前只有用剥层法测定剥露出来的表面应力，再进行校正。剥层后剥露面上所测应力不是原来的残余应力，而是释放后的应力（剥除时不允许因加工产生新的附加应力）。用弹性力学计算测定值的校正量，得到原来的应力值。

1.校正公式

（1）厚壁圆管和圆柱的校正公式。

1）基本假定。工件可以近似看作厚壁圆管或圆柱，轴径比超过6倍，在所测部位残余应力分布是轴对称，且沿轴向分布是均匀一致，即残余应力仅是半径的函数。剥层时，轴的外表面对称剥离，应力分布仍保持轴对称性不变，即剥除前后同一截面的平面保持不变。

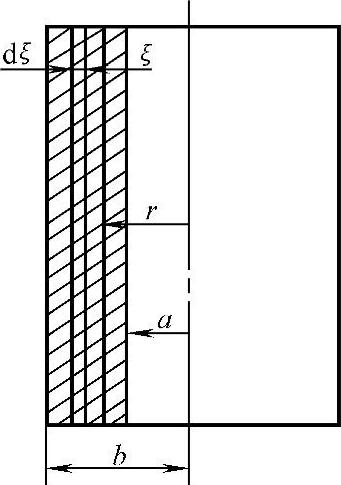
图8-41 圆管的外剥层

2）校正公式。取一厚壁圆管（图8-41），外半径为b，内半径为a，外表面剥层后的半径为r，在r处测得的轴向应力为σ′_zr，切向应力（也称周向应力）为σ′_τr，校正量为Δσ_zr和Δσ_τr，原来此处的残余应力为

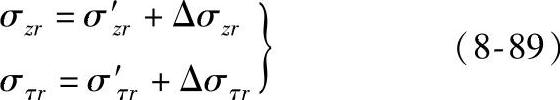
令任意处半径为ξ，经弹性力学推导得到厚壁圆管的校正公式如下：

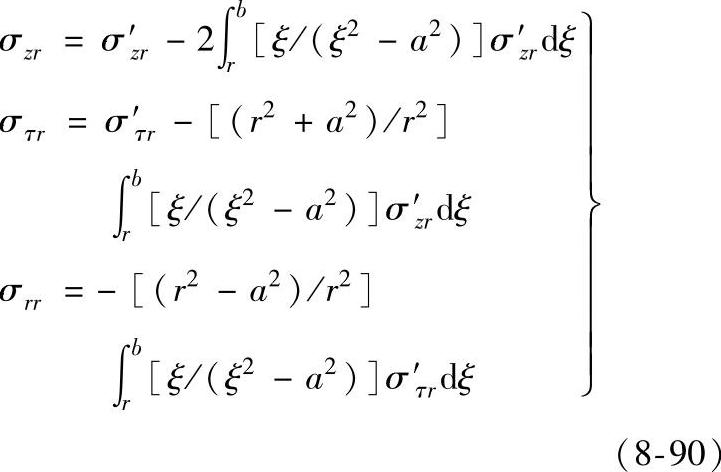
其中，σ_zr为轴向应力；στr为切向应力；σ_rr为径向应力，注意到表面处有σ_rr=0，在剥露表面就测不到σ_rr，只能计算出来剥离时此处的σ_rr。

对于圆柱试样，则只需式（8-90）中a=0即可。

（2）平板的校正公式。

1）基本假定。所测工件能近似看作长、宽远大于厚度的平板，残余应力的分布仅是板厚的函数；在任意垂直于板厚度的平面上应力值是相同的；剥层后该平面仍保持平面不变。

2）校正公式。平板的剥层如图8-42所示。若板长、宽远大于厚度，则在距边缘三个厚度以上的区域测定应力时，可将板看成是无限大平板。现从板的下表面单侧剥除。当剥离到z处时，设该处原来的应力为σ_x（z）、σ_y（z），而剥露处表面上测定的应力为σ′_x（z）、σ′_y（z），剥层前后应力释放量为Δσ_x（z）、Δσ_y（z）。由于是单侧剥层，因抗拒附加弯矩产生的附加应力为Δσ_Mx（z）、Δσ_My（z），所以剥除前此层的残余应力为

经弹性力学推导整理后其公式如下：

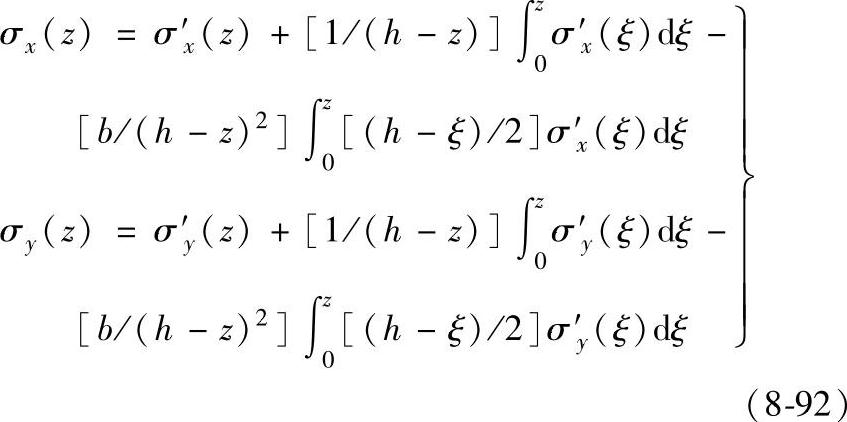
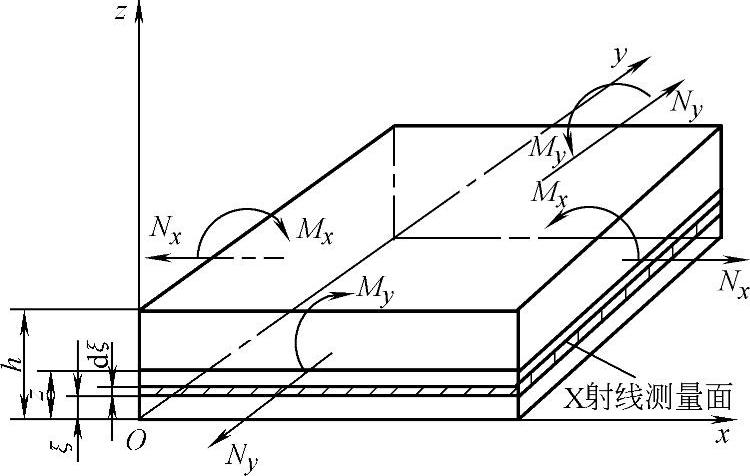
图8-42 平板的剥层

其中，δ_zr为轴向应力；σ_τr为切向应力；σ_rr为径向应力，注意到达表面处有σ_rr=0，所以在剥露表面就测不到σ_rr，只能用测出的σ_zr和σ_τr利用弹性力学计算出未剥离时此处的σ_rr。

2.测定方法

（1）剥层方法。

1）机械法。在每次剥层深度大于0.1mm时可采用机械法（车、铣、磨等），但必须留下0.1mm左右的余量用不产生附加应力的腐蚀法去除。即使如此，机械法剥层时，切削用量不能太大，必须在加工中充分润滑冷却，以减少切削热和切削应力的影响。

2）电化学腐蚀法。当剥除量很小时（如＜0.1mm）应采用腐蚀法，以保证不改变剥露表面的应力值。

当采用恒电位法时，一般的钢铁材料常用的电解液为w（H₃PO₄）=50%的水溶液（pH=1.0）。

3）化学腐蚀法。这种方法的关键是选择腐蚀剂，一般钢铁材料可采用的腐蚀剂配方为：150mL硝酸+50mL过氧化氢+20g草酸，然后加水至500mL。但本方法不适用于高合金钢，特别是不锈钢。对于这些材料只能用前述的电化学腐蚀。

上述两种腐蚀法剥层时必须注意反应时的温度控制，一般以＜70℃为宜，否则会出现蚀坑使表面粗糙度大大提高，影响测试精度。

另外，每次腐蚀时间不宜过长，一般以3～5min为宜，每腐蚀一次必须将工件从腐蚀液或电解液中取出，并将表面沉积的物质冲洗干净，这样才能保证腐蚀的表面质量。

（2）应力测定方法。一般应采用F射线应力测定法，因为它测定的层深最浅。

3.计算方法 计算公式（8-74）和式（8-76）均为积分方程，因此可用每次的剥层深度作为步距，用不等距梯形面积法的求和以代替求积，从而求得函数的积分值。