常用残余应力测试方法优化

在此对工程中常用的几种残余应力测试方法作一些简要介绍，并对热处理工件最常用的F射线法作较详细的介绍。

8.3.2.1 钻孔法

本方法是在工件欲测点周边先做上测定应变的标记或贴上电阻应变片，然后在测点处用钻头（或用高压喷沙嘴）在测点处打出一圆孔，使孔的相邻区域应力因钻孔处应力释放而产生重新分布，从而产生相应的位移和应变，通过测量此位移和应变，经换算即可得钻孔处原来的残余应力值和方向（主应力）。过去是测标点位移来求应变，目前已主要用电阻应变片来测定。

1.测定原理 设工件为一无限大平板，在点O处打孔，在点A处贴应变片，如图8-14所示。若主应力为σ₁、σ₂（σ₁≥σ₂），则点A处的应力分量为

若点O处打一直径为a的通孔，则点A处应力分量为

因而由于钻孔引起的应力改变量为

图8-14 钻孔法示意图

点A处将相应地产生释放应变，且有

ε′_r=（σ′_r-μσ′_t）/E （8-4）

将式（8-3）代入式（8-4）即可得点A处径向应变ε′_r与主应力σ₁和σ₂之间的关系。这样在点O的附近等距离贴上三个应变片A、B、C（图8-15），其测出的径向应变为ε′_rA、ε′_rB、ε′_rC，即可由此求出主应力σ₁、σ₂与主应力方向φ。将式（8-3）代入式（8-4）后经整理可得

ε′_r=A/E（σ₁+σ₂）+（B/E）·（σ₁-σ₂）cos2φ （8-5）

其中

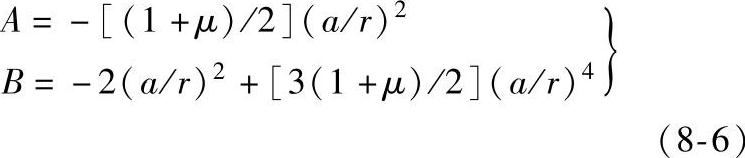
式中 r——孔中心到应变片中心的距离。

设A、B、C应变片与主应力σ₁夹角分别为φ-α、φ、φ+α，依据式（8-6）得三点的径向应变为

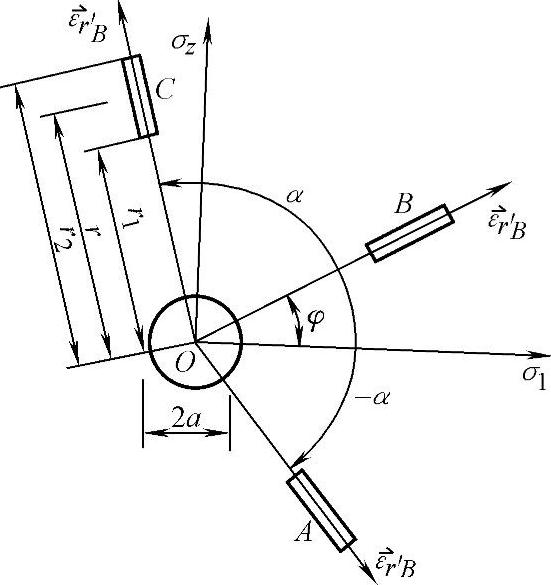
图8-15 径向应变的电测

解式（8-7）求得σ₁和σ₂与测定的径向应变ε′_rA、ε′_rB、ε′_rC之间关系为

tan2φ=tanα[（ε′_rA-ε′_rC）/（2ε′_rB-ε′_rA-ε′_rC）] （8-9）

当A、B、C每隔45°粘贴应变片时，即α=45°，代入式（8-8）得

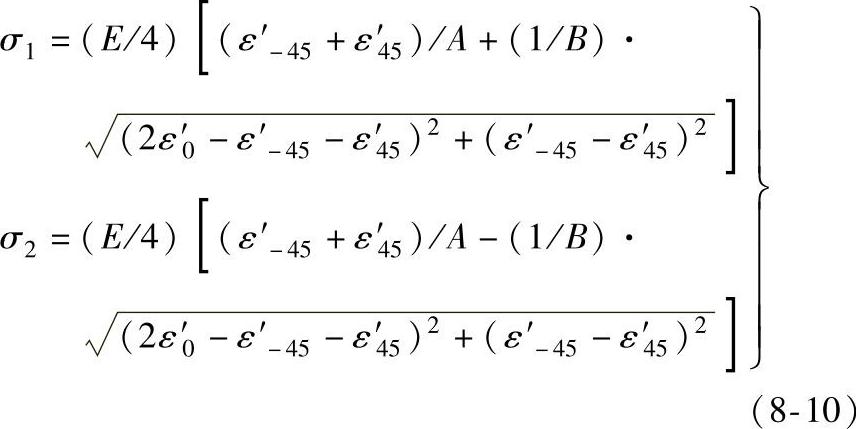
tan2φ=（ε′_-45-ε′₄₅）/（2ε′₀-ε′_-45-ε′₄₅） （8-11）

若α=120°，则有

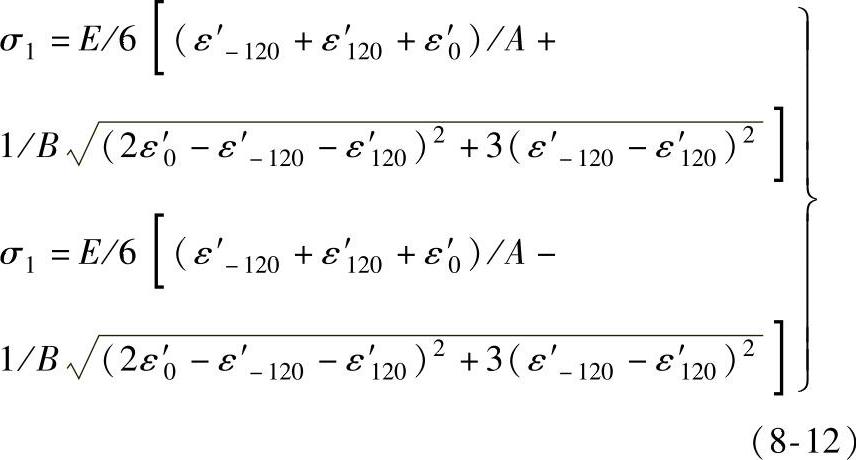
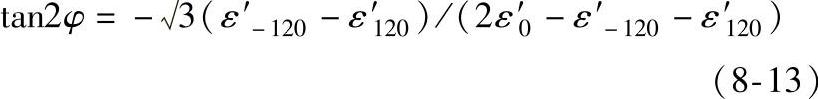
2.测定方法

（1）根据应力分析的需要和打孔的可能，在工件上选择适当位置进行测量，然后用测量工具准确地标定出孔中心和应变片的中心和方向。在贴片前需将所测部位表面打磨抛光。

（2）按确定的位置和方向粘贴应变片，用导线连接至电阻应变仪。按电阻应变仪测定的规程进行测定。

（3）然后钻孔，直径一般小于ϕ2mm。为了减少附加应力和发热的影响，孔可分为两次钻削，即先钻一小孔，再扩至所需直径。钻头需锋利，进给量不能太大，一般不超过0.1～0.15mm/min。

（4）在A、B、C三点测得三个方向的径向应变ε′_rA、ε′_rB、ε′_rC，代入前述的式（8-8）～式（8-13），即可求出残余应力。

（5）测试前必须将所测材料做成平板拉伸或弯曲试样，在万能试验机上加载，然后用同样方法测ε′_rA、ε′_rB、ε′_rC，这时应力σ和方向2φ为已知，可代入公式，求出A、B的值。对于不同材料必须用此法标定其不同的A、B值。

3.不通孔法（在早期测试报告、论文、专著中称其为“盲孔法”）为了减小所钻小孔对工件的破坏，可用钻不通孔的方法。根据理论分析和实测证明，当孔的深度超过孔直径的2倍后，对孔周边表面的应变无任何影响，即当孔深大于2倍直径后应变片测量值无变化。所以在孔深大于2倍直径的条件下，对于不通孔仍可用上述通孔的公式。为了减小孔的破坏，孔径可尽量小，这样孔深也可减小。如孔径为ϕ2mm时，孔深为4mm；而孔径为ϕ1mm时，其孔深就只需2mm。目前还有采用浅不通孔的方法，即孔深小于2倍直径。这时的A、B系数值随孔深变化，因此必须将该材料A、B系数随孔深变化的规律求出才能测定。而目前还找不到解析法，只能用试验法和有限元法进行标定，试验法精度难以保证，有限元法则非常麻烦。所以目前浅不通孔法应用还有困难。

关于应力释放法和钻孔法进行残余应力测定的详细方法和计算，读者可参阅相关文献。

4.脆性涂层法 它是在孔周涂覆0.5～2mm厚度的脆性涂层，然后钻孔。由于产生的位移和应变将使涂层产生裂纹（理论上说裂纹的形态和应力方向相应），故裂纹的长度大小与应力大小有关。但目前此方法的定量分析还只是理论上的，其测量精度尚难以保证。图8-16所示为脆性涂层在孔边的裂纹形态和应力状态的关系。

8.3.2.2 磁性法

1.基本原理 本方法只能用于钢、铁类铁磁性物质，它是利用这类物质的磁弹性效应来测定材料表面1～2mm层深的残余应力。

（1）磁致伸缩和磁弹性效应。铁磁物质中软磁性材料具有磁致伸缩效应，它是因磁畴在外磁场H作用下的转向，使材料在不同方向上产生尺寸的增大或减小。若材料受外界约束或受应力作用（如残余应力），则磁致伸缩将受阻碍，这时和无阻碍材料相比则磁化率将减小，其磁导率μ和应力σ之间有如下的正比关系：

Δμ/μσ=λ₀μ₀σ（8-14）

图8-16 脆性涂层在孔边的裂纹形态和应力状态的关系

a）单向拉伸 b）双向拉伸 c）单向压缩 d）双向压缩

式中 λ₀——初始磁致伸缩系数；

μ₀——无残余应力时的磁导率；

μ_σ——有残余应力时的磁导率；

σ——材料的残余应力。

式（8-14）即称磁弹性现象，它相当于这时的胡克定律。Δμ=μ₀-μ_σ为磁导率的变化量，所以Δμ/μ_σ即为磁应变。对于每种材料，只要测定了无应力下的λ₀和μ₀，则利用式（8-14）即可通过测定磁应变Δμ/μ_σ来求残余应力σ。(www.xing528.com)

（2）应力和磁滞回线的关系。无应力的材料无论从哪个方向做磁滞回线都应当是一样的，也就是磁是各向同性的。但由于残余应力对磁导率有影响，所以在不同方向磁化时其磁导率就不同，其磁滞回线也将不同，沿拉伸应力方向磁滞回线变大，垂直拉应力的磁滞回线变小。如果是压应力，则与其变化相反（图8-17）。利用此原理可求得材料中的主应力方向。

图8-17 低碳钢在拉、压应力作用下表现的磁各向异性

2.测定方法

（1）传感器和应力测定。测材料磁导率变化所用的传感器，如图8-18所示。它是由软磁材料铁心和外绕线圈组成。其铁心成框形不封闭，当探头与工件密合后其磁感应成闭合回路。

设探头磁导率为μ₁，试样的磁导率为μ₂，探头磁路长为L₁，试样的磁路长L₂，探头和试样各自的磁阻为R₁和R₂，试样磁路和探头磁路的截面积分别为S₁和S₂，则总磁阻为

R=R₁+R₂=L₁/μ₁S₁+L₂/μ₂S₂ （8-15）当试样中有应力时，μ₂就发生变化，这就引起R₂变化，这样探头的阻抗也就随应力的大小而变化，若能测出阻抗的变化就能测出应力。

图8-19所示为磁法测量的线路图，其桥式电路就可测出探头的阻抗变化。在无应力状态下使测量探头和补偿探头的阻抗平衡，这时电路是平衡的，电流表mA无读数。若测量探头改放在有应力的试样上，由于应力使μ₂发生变化，从而使测量探头一侧阻抗发生变化，使原来平衡的电路不平衡了，这样电流表mA将有读数，其电流I的大小取决于被测材料的应力，只要求得电流I与应力的关系则应力可测。

图8-18 传感器示意图

图8-19 磁法测量的线路图

（2）平面应力的测定。工件表面的应力状态均为平面应力状态，所以用磁测法测定的均为平面应力。在平面应力状态下垂直表面的应力σ₃为零，其主应力只有σ₁和σ₂，其大小和方向如图8—20所示。欲测点为O，建立坐标轴Ox、oy，设主应力方向分别为且的夹角为θ，探头的两个磁极分别在m(a，O)和-m（-a，O）处。

1)主应力方向的测定。将探头以()点为中心旋转，当0=0。时，轴重合，方向就是最大主应力σ₁，的方向，对应的磁化强度和磁导率都最小，因此输出电流I也最小。反之若探头转到O_η方向，则对应的是最小主应力σ₂，所以其磁化强度和磁导率是所有方向中最大的，因而输出电流也最大。旋转磁头找到测量线路中输出的电流I的极小和极大值，就可求得对应的最大主应力σ₁和最小主应力σ₂的方向。

图8-20 平面应力测定时主应力的大小及方向

2）主应力值的测定。此时主应力差（σ₁-σ₂）与主应力方向的输出电流差（I₂-I₁）成正比，即

（σ₁-σ₂）=（1/α）（I₂-I₁）

式中的α为灵敏度系数，有

α=（I₂-I₁）/（σ₁-σ₂） （8-16）

而α与材料的成分和处理状态有关，所以在实测前，必须对成分和处理完全相同的无应力材料通过加载来求其灵敏度系数α。对此材料施加不同的拉应力和压应力，测出对应的I₁和I₂，然后作出（I₂-I₁）和（σ₁-σ₂）的曲线。当然，所测数据必然有起伏偏差，所以其直线斜率可用作图法或最小二乘法求得。此即为灵敏度系数α，其单位为_μA/MPa。

有了主应力差和主应力方向，可用切应力差法求得主应力值。它的作法如图8-21所示。在边沿取一点O为起始点，然后在一定的Δy范围内，并以一定的Δx间距，取n个点，过点求得其切应力差Δτ_xy，再过点递推地求得其（σ_x）_i，再根据（σ_y）_i与（σ_x）_i和（σ₁-σ₂）的关系求得（σ_y）_i，这样有了（σ_x）_i、（σ_y）_i和θ_i，即可求得相应的（σ₁）_i和（σ₂）_i。为了便于求解，坐标原点O最好如图8-21所示取在试样的自由边，这时（σ_x）O=0。

图8-21 切应力差法求主应力示意图

二维应力场的平衡方程为

根据图8—21，将上式从O点到n点取积分，第n点的σ，值为

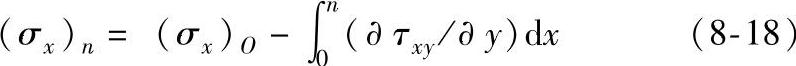
将积分项用差分和代替，得

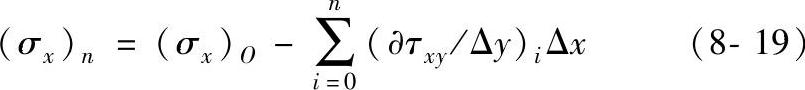
其中，（σ_x）O为O点的σ_x值；（∂τ_xy/Δy）i^Δx为从

O点到n点的（Δτ_xy）i（Δx/Δy）各项之和；（Δτ_xy）i为沿x轴每增加一个（Δτ）_xyiΔx时，切应力τ_xy沿Δy的增量，即间隔Δx的上辅助面AB和下辅助面CD的切应力差值。当设定了Δx和Δy的大小后，（Δx/Δy）之比值为常数。为了求得各点的应力状态，我们是采用逐点递推求和的办法首先求得各点的（σ_x）_i值，即

大括号中的项为相邻两点的切应力平均值。（σ）_i为欲求的第i点的σ_x值，（σ_x）_i-1为已求出的前一点的σ_x值，而

于是根据各组的（σ_x）_i、（σ_y）_i及θ_i，可求得所对应的（σ₁）_i及（σ₂）_i。

至于τ_xy则可由下式确定，即

τ_xy=[（σ₁-σ₂）/2]sin2θ_i （8-22）而剪应力差Δτ_xy则为

Δτ_xy=（τ_xy）上-（τ_xy）下 （8-23）

3）测定步骤

①从欲测试样边沿（此处为σ_x=0）或某已知应力的点开始，以Δy为宽度、Δx为间隔n个点。

②用仪器测出各点的主应力方向θ_i。

③根据标定的灵敏度系数α和各点的（I_2-I₁）_i，求出其对应的（σ₁-σ₂）_i。

④按式（8-22）计算（τ_xy）_i。

⑤按式（8-23）计算（Δτ_xy）_i。

⑥据式（8-20）计算（σ_x）_i，注意测定中必须使（σ_x）_O为已知。

⑦据式（8-21）计算（σ_y）_i。

⑧再据弹性力学可知，对于平面应力状态，σ_x+σ_y=σ₁+σ₂，所以主应力之和可以求出，而主应力之差已测出。据此可求得σ₁和σ₂的值。

注意：若试样是处于拉—拉或压—压的平面应力状态，则测试方法可大为简化。因为主应力和与电流和成正比，因此只要再加前述的标定试验求得灵敏度系数α′，就可直接用输出电流求得主应力和，求解这组联立方程就可得到σ₁和σ₂。

测试仪器有长江科学仪器厂生产的CY-1型仪器（由上海交通大学设计）和邯郸无损探测仪器厂生产的CCY-84型仪器（由西安交通大学设计），这两种仪器均适用于大型构件的现场测试。