金属应力松弛的松弛稳定性及测定方法

6.8.2.1 应力松弛现象

动力机械中有许多零件，例如汽轮机和燃气机组合转子或法兰的紧固螺栓，高温下使用的弹簧、热压部件等，都是在应力松弛条件下工作的（图6-177）。所谓松弛是指零件或材料在高温下总形变不变，但其中所加的应力却随着时间增长而自发地逐渐下降的现象。

图6-177 零件高温下使用产生应力松弛

金属材料的高温松弛也是由于蠕变现象引起的。在松弛的试验或工作条件下，总应变ε₀（包括弹性应变ε_e和塑性应变ε_p）是恒定的，即

ε₀=ε_e+ε_p=常数 （6-108）在高温试验过程中，由于发生蠕变，塑性应变不断增大，则ε_e不断降低，随之应力σ（=Eε_e）也不断降低。

若将蠕变与松弛过程进行比较，如图6-178所示，就能搞清楚松弛现象。

蠕变时，应力保持不变，塑性形变和总形变随时间增长而增大。而松弛时，总形变不变，随时间增大，塑性变形不断地取代弹性形变，使弹性应力不断下降。虽然它们的表现形式不同，但两者在本质上并无区别，因此松弛现象可看做是一种在应力不断减少条件下的蠕变过程，或者说是在总应变量不变条件下的蠕变。蠕变抗力高的材料，应力松弛抗力一般也高，但不能从蠕变的数据直接推算出应力松弛的情况，因此一般蠕变并不能代替应力松弛。

图6-178 蠕变和松弛现象的比较

a）蠕变 b）松弛

6.8.2.2 松弛稳定性指标及其测定方法

金属应力松弛试验方法在GB/T 10120—1996中有详细的规定。应力松弛过程可以通过应力松弛曲线来描写。在恒温和总应变恒定的条件下，测定应力时间的关系，可以得到如图6-179所示的σ-t曲线，这曲线称为应力松弛原始曲线。曲线第一阶段应力随时间急剧降低，第二阶段应力下降逐渐缓慢并趋于恒定。在第二阶段，σ-t的关系可用下述经验公式来表示：

式中 σ——剩余应力；

σ′₀——第二阶段的初始应力；

t——松弛进行时间；

t₀——与材料有关的常数。

图6-179 应力松弛原始曲线

若式（6-109）用lgσ-t半对数坐标作图，则可得如图6-180所示的应力松弛曲线。图中明显划分为两个阶段，第二阶段为一直线。因此在第二阶段内，可以通过较短时间的试验后进行外推，从而求得较长时间的剩余应力。

图6-180 松弛曲线

材料抵抗应力松弛的能力称为松弛稳定性。松弛曲线第一阶段中的松弛应力，用s₀=σ₀′/σ₀表示，其中σ₀为初应力，σ₀′可由松弛曲线的直线部分与纵坐标的交点来确定。材料第二阶段的松弛应力用t₀=1/tanα表示。

显然，s₀、t₀值越大，则材料的松弛稳定性越高。同样若式（6-109）用σ-lgt半对数坐标表示（图6-181），则σ₀越大，应力下降速度也越大。经过长时间松弛后，剩余应力相当接近。

图6-181 松弛曲线(www.xing528.com)

由式（6-108）得：

其中，应力下降率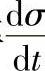由图6-180中曲线求出，代入式（6-110）便可得到ε·_p与σ的关系（图6-182）。

图6-182所示的曲线也表示应力松弛，它可以分为两个阶段。第一阶段的塑性形变速率ε·_p同时取决于应力和塑性形变；而第二阶段几乎与应变没有关系，仅仅取决于应力。已知在蠕变第一阶段的形变速率也取决于应力和塑性形变，而蠕变第二阶段时仅仅取决于应力。这表明应力松弛的第一、第二阶段与蠕变的第一、第二阶段相似的关系。

图6-182 应力-塑性变形速度曲线

应力松弛试验若在应力、应变均能自动控制的Hnstron型电子拉伸机上进行，则十分简单（图6-183）。一定的温度环境通过电阻炉加热实现；应力、应变通过载荷传感器和引伸机与电子控制系统来实现。可以用引伸仪监控试样标距长度，使其恒定不变。当长度发生变化时，应力便会自动降低，使其标距又回到原来的长度，并能自动记录σ-t曲线。

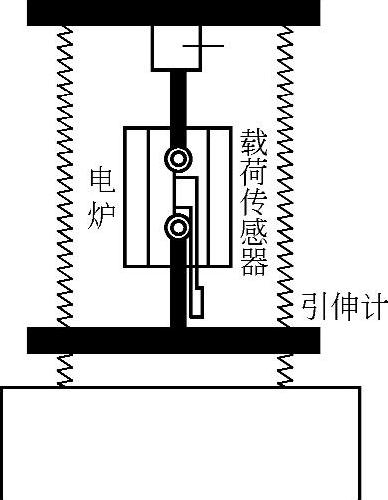
图6-183 松弛试验

如果没有上述试验机，可采用一般蠕变试验机进行降压法试验（也称Kobinson法），如图6-184所示。首先施加初始压力，使总应变ε₀达到预定的数值之后，适当地减少应力（设为σ₁），进行恒应力σ₁下的蠕变试验。当总应变又达到ε₀之后，再重复上述过程，分成不同的应力阶段（σ₁、σ₂、σ₃…）进行松弛试验。试验表明，这种方法在实用上是可靠的。

也可以采用环形试样进行应力松弛试验，其试样的形状和尺寸如图6-185所示。施加载荷时只需将楔子（K）插入开口C中即可。由两个偏心圆所形成的试样工作部分（BAB）与等弯矩梁的形状相当，而与间隙相毗邻的非工作部分（BCB）仅为传递外加力矩之用。为了保证刚性，这部分截面较大，以致可将其弹性忽略不计。借助金刚石压锥在试样非工作部分刻出的标记，仔细测量环形试样开口宽度，插入楔子，将试样放入炉中加热，经一定时间后取出冷却并将楔子拿出，然后重新测量开口的宽度。

图6-184 降压法试验的原理

图6-185 应力松弛试验用环形试样

a）试样 b）楔子

由于试样工作部分塑性变形的增加，开口宽度随时间而增大。按照开口尺寸的改变可以计算应力大小并绘制应力-时间关系曲线。

环形试样加载应力σ为

σ=AEΔ （6-111）

式中 A——系数，对于上述形状尺寸的试样，其数

值为0.000583/mm；

E——试验温度下材料的弹性模量；

Δ——Δ=c₂-c₁，其中c₁为试样间隙原有宽

度，随试验时间的延长而逐渐增大，c₂为楔子插入后的宽度，为一定数。

图6-186所示为各种材料经1000h，总应变约为0.2%的应力松弛曲线，可供设计参考。