最常用的表明零件或材料疲劳抗力性质的方法是疲劳曲线,即所加应力σ与断裂前循环周次N(疲劳寿命)之间的关系曲线,通常用σ-lgN表示,如图6-114所示。
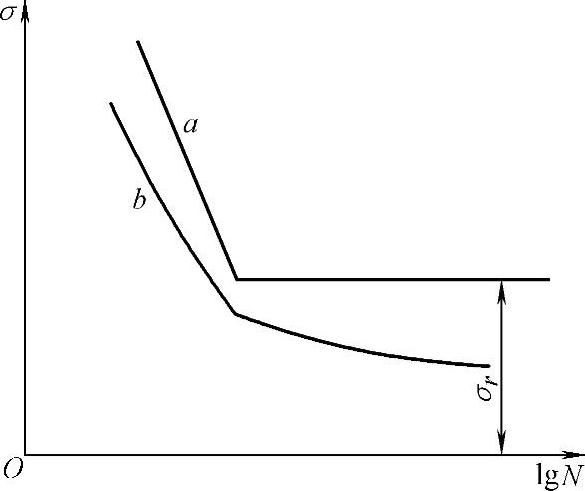
图6-114 疲劳曲线
6.6.2.1 疲劳极限与过载持久值线
疲劳曲线表明,应力水平σ高时,疲劳寿命N短;σ低时则N长。当应力低到某一定值时,虽经历很长的循环周次,也不再发生疲劳断裂,如曲线a这样的应力称为疲劳极限,用σ-1表示(脚注-1表示对称循环);如果不是对称循环,则依对称系数r写成疲劳极限为σr。应力循环经过107次不发生疲劳断裂,即认为不再断裂,故107为一般疲劳试验的基数。对高强度钢、铜、铝等金属材料,腐蚀介质下以及大截面试件,无明确的疲劳极限,这时规定经历5×106、107或108次循环而不断的最高应力为条件疲劳极限,如图6-114中曲线b所示。疲劳极限是对要求无限寿命的机件进行疲劳设计的重要依据。最常作的疲劳试验是平面弯曲、旋转弯曲和轴向拉压加载的疲劳试验。如未注明,则疲劳极限数据是在对称循环、旋转弯曲加载试验条件下得到的。
材料的疲劳极限σ-1与抗拉强度Rm之间有较好的相关性,不进行试验,σ-1可用Rm近似估算。
碳钢和合金钢的对称弯曲疲劳极限σ-1,一般可用下面形式的公式近似计算:
σ-1=a+bRm (6-80)对Rm<1400MPa的碳钢和合金钢,推荐使用如下关系式:
σ-1=38MPa+0.43Rm (6-81)还有一些更精细的经验公式:
正火和退火碳钢σ-1=8.4MPa+0.454Rm (6-82a)淬火、回火碳钢σ-1=-24MPa+0.515Rm (6-82b)淬火、回火合金结构钢σ-1=94MPa+0.383Rm (6-82c)
σ-1与Rm的关系,也可写成如下形式:
σ-1=cRm (6-83)c称为疲劳比。常用金属材料的疲劳比见表6-34。
表6-34 常用金属材料的疲劳比

σ-lgN曲线的斜线部分,称为过载持久值线,可用下式表达:
σmN=c (6-84)通常在σ-lgN或lgσ-lgN坐标中用直线段来近似表达。它表示对有限寿命的疲劳抗力,是对要求有限寿命机件的疲劳设计依据。对于要求无限寿命的零件,在工作过程中,也有超载运行的情况,过载持久值线则表明材料承受这种偶然超载运行的能力。过载持久值所表示的过程是疲劳裂纹萌生、扩展以至断裂的过程,现在已广泛采用断裂力学方法来表示材料疲劳裂纹扩展行为,这部分内容在本节疲劳累积损伤一段中还要提到。
6.6.2.2 p-σ-N曲线
由于疲劳试验数据的分散性,试样的疲劳寿命与应力水平间的关系,并不是一一对应的单值关系,而是与存活率p有关系。用常规方法做出的σ-N曲线,只能代表中值疲劳寿命与应力水平间的关系。要想全面表达各种存活率下的疲劳寿命与应力水平间的关系,必须使用p-σ-N曲线。
在利用对数正态分布或威布尔分布求出不同应力水平下的p-N曲线以后,将不同存活率下的数据点分别相连,即可得到一族σ-N曲线,其中的每一条曲线分别代表某一不同存活率下的应力寿命关系。这种以应力为纵坐标,以存活率p的疲劳寿命为横坐标,所绘的一族存活率-应力-寿命曲线,称为p-σ-N曲线,如图6-115所示。在进行疲劳设计时,即可根据所需存活率p,利用与其对应的σ-N曲线进行设计。
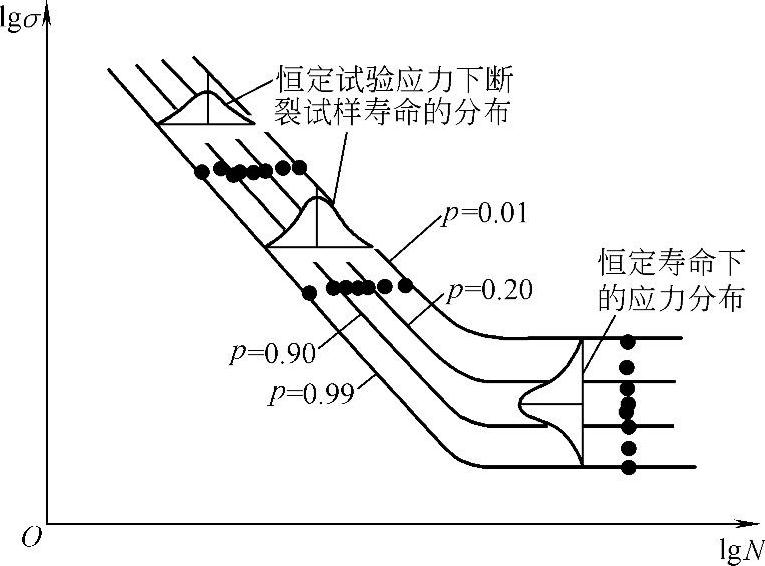
图6-115 p-σ-N曲线示例
6.6.2.3 疲劳缺口系数Kf
由于机器零件大都具有截面变化,例如键槽、油孔、轴肩及螺纹等,因此会产生应力集中,使疲劳极限降低。为表明应力集中对疲劳极限的影响程度,定义Kf为“疲劳缺口系数”,亦称“有效应力集中系数”。

式中的σ-1是光滑试样疲劳极限;σ-1n是缺口试样疲劳极限。Kf、σ-1n当然与缺口的具体形状,如缺口深度、缺口根部圆角半径等参数有关。由于缺口形状变化复杂,为避免大量的试验工作,工程上常采用一些公式计算Kf。
现在常用的Kf计算式有Eeuber公式:
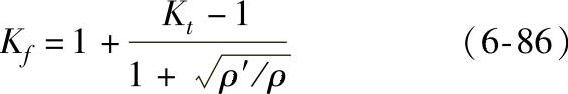
和Peterson公式:
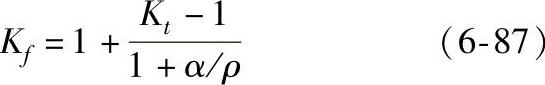
式中的Kt为理论应力集中系数;ρ为缺口根部曲率半径;在接近疲劳极限的长寿命区,ρ′和α为材料常数,取决于材料的强度和塑性;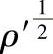 值可由图6-116查出;
值可由图6-116查出;
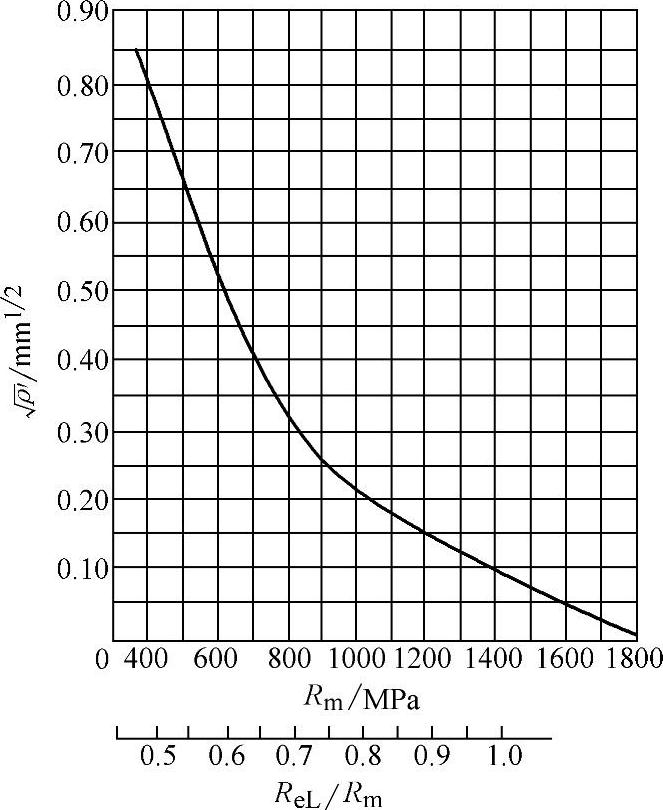
图6-116 Neuber参数图
α值依Peterson的资料,对回火钢为0.0635,对正火钢为0.254,对铝合金为0.635。
郑州机械研究所赵少汴等人得出的Kf计算式,与多钢种、宽范围的Kt值的试验结果符合良好。
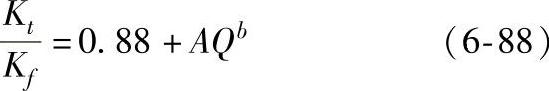
式中的Q为相对应力梯度(mm-1),对于常见几何形状零件可使用表6-35中的公式计算,b、A是与热处理状态有关的常数,常用结构钢正火态A为0.423,b为0.279;热轧态A为0.336,b为0.345;淬火后回火态A为0.290,b为0.152。
6.6.2.4 不对称应力循环的疲劳图
如图6-113所示,不对称应力循环可分解成恒定应力σm和对称循环应力σa两部分。可将不同平均应力σm情况下的疲劳极限σmax以及相应的σmin绘成如图6-117所示的不对称循环疲劳图ABF。AB和FB线从试验得出,可能是粗线所示的直线关系(Good-man直线),也可能是细线所示的抛物线关系(Ger-ber抛物线),当应力超过屈服强度ReL(规定塑性延伸强度Rp0.2)时,以ReL(Rp0.2)作为设计应力,则得到ACDEF。
表6-35 某些常见应力集中情况的相对应力梯度Q值

注: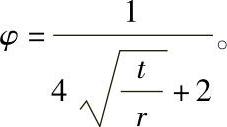
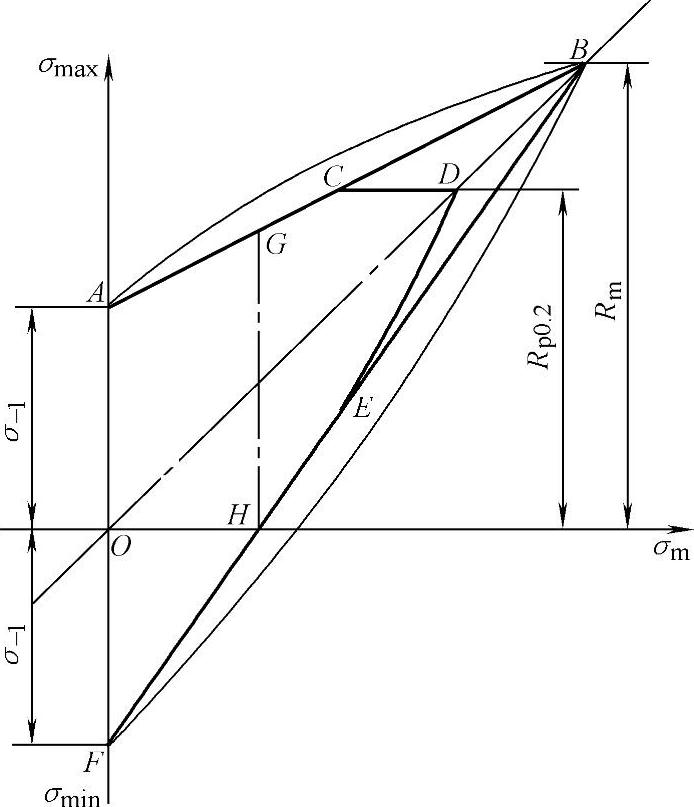
图6-117 不对称循环疲劳图
实用中还常用σa-σm曲线表示不对称循环疲劳图,如图6-118所示。
如果要求表示的不是与无限寿命相当的疲劳极限,而是与一定有限寿命相当的不对称循环疲劳性质,则可绘制如图6-119所示的等寿命曲线图。
表6-36所示为7种国产钢不同应力比下的拉-压疲劳极限。(https://www.xing528.com)
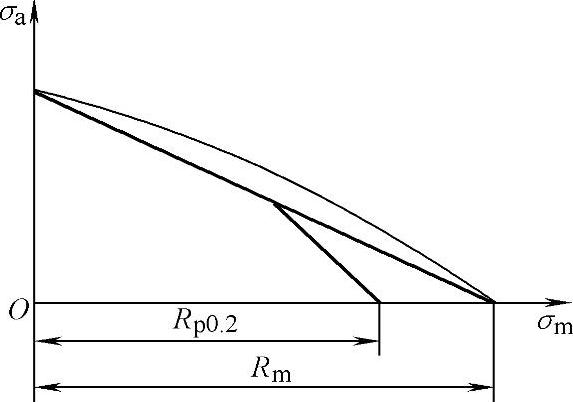
图6-118 用σa-σm曲线表示的不对称循环疲劳图
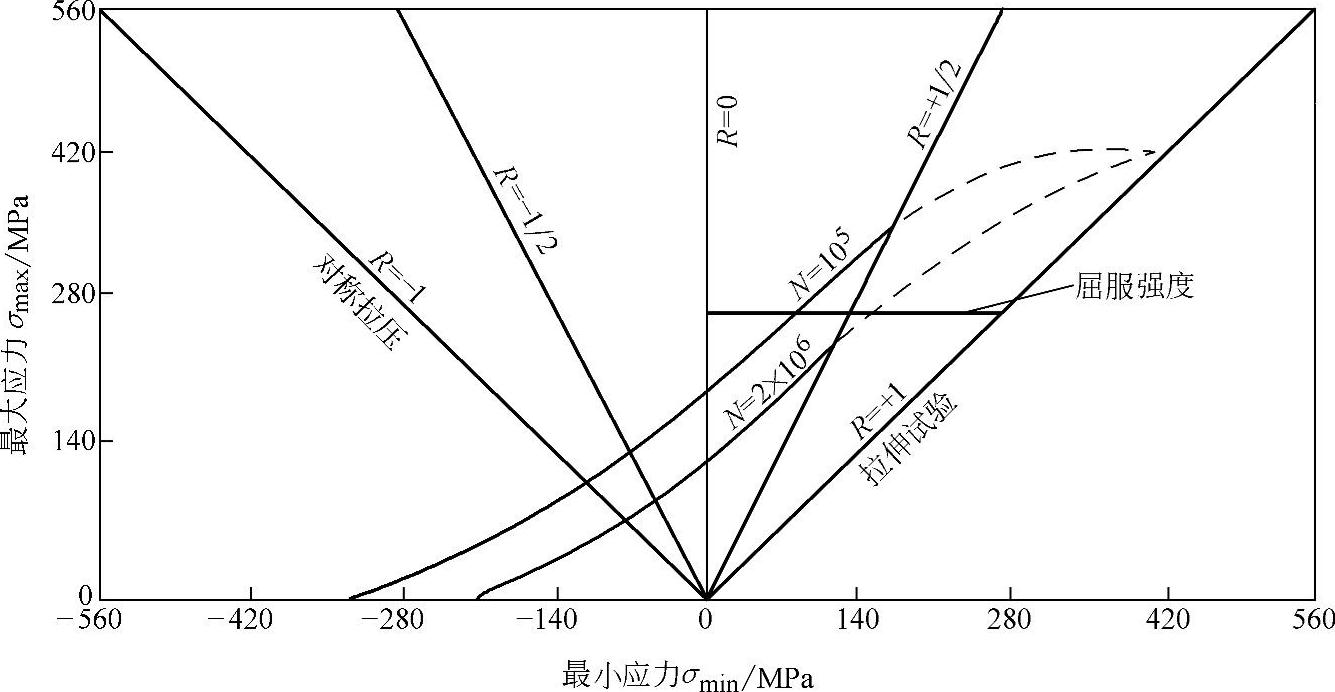
图6-119 等寿命曲线图
表6-367 种国产钢不同应力比下的拉-压疲劳极限 (单位:MPa)
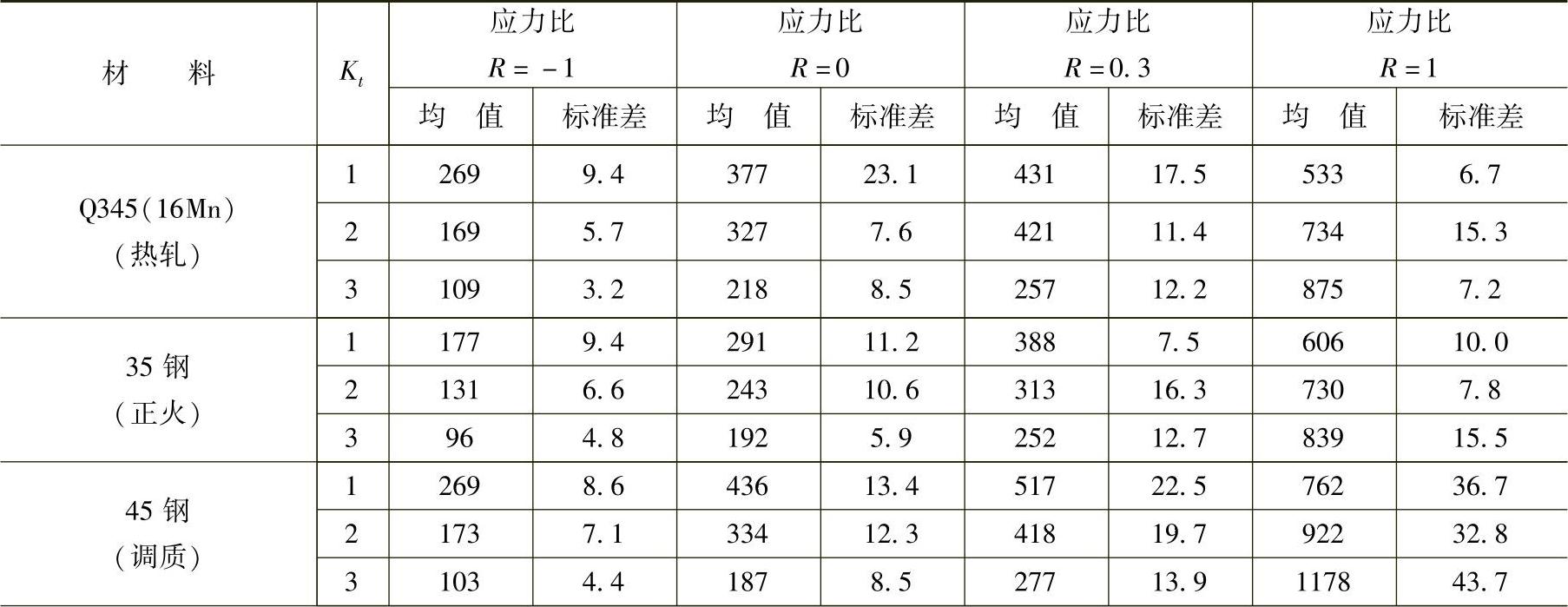
(续)

6.6.2.5 疲劳累积损伤
大多数零件都是在变幅载荷下工作。变幅载荷下的疲劳破坏,是不同频率、不同幅值的载荷所造成的损伤逐渐积累的结果。每一循环所造成的损伤可以认为是在此载荷幅值下循环寿命N的倒数1/N,这种损伤是可以积累的。n次恒幅载荷循环所造成的损伤等于其循环比c=n/N。变幅载荷循环所造成的损伤D等于其循环比之和,即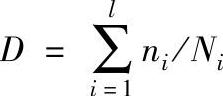 (其中:l为变幅载荷的应力水平级数,ni为第i级载荷的循环次数,Ni为第i级载荷下的疲劳寿命)。当D达到临界值DC时,发生疲劳破坏。
(其中:l为变幅载荷的应力水平级数,ni为第i级载荷的循环次数,Ni为第i级载荷下的疲劳寿命)。当D达到临界值DC时,发生疲劳破坏。
现在工程上有很多种估算变幅疲劳累积损伤的方法,通用的是Miner法则,即
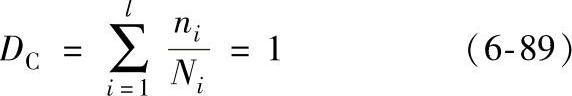
精确的研究表明,DC值并不等于1,通过一些实际零件变幅循环疲劳破坏的统计,得到不等于1的更为符合实际的DC值a时,则称为修正的Miner法则,有的文献推荐,a值取为0.7,其寿命估算结果比Min-er法则安全,寿命估算精度比Miner法则有所提高。
6.6.2.6 低周疲劳
桥梁、容器、船舰、车辆和飞机等的机件在工作过程中,除正常的较低应力幅的应力循环外,还常常受到较大应力幅的循环。这样的应力幅往往接近或超过材料的屈服强度,使构件某些局部甚至整体产生较大的反复塑性变形。这种由于反复循环塑性变形造成的疲劳破坏使其寿命比通常应力较低的疲劳寿命短,循环周次为102~106,称为“低周疲劳”,也称“高应变疲劳”或“塑性疲劳”。
在讨论低周疲劳时,首先要提到循环载荷作用下材料的应力与应变的关系,即循环应力应变曲线。金属在弹性范围加载,其应力应变是可逆的;当加载超过弹性范围时,应变落后于应力,形成应力应变滞后回线。在循环加载初期,应力应变回线并不封闭,它的形状随循环次数而变,只有经过一定周次循环后,才形成封闭的稳定的滞后回线。将应变幅控制在不同的水平上,可以得到一系列大小不同的稳定的滞后回线,将其顶点连接起来,则可得到材料的循环应力应变曲线。循环应力应变曲线,是不同应变或应力幅情况下滞后回线顶点的轨迹,如图6-120所示。
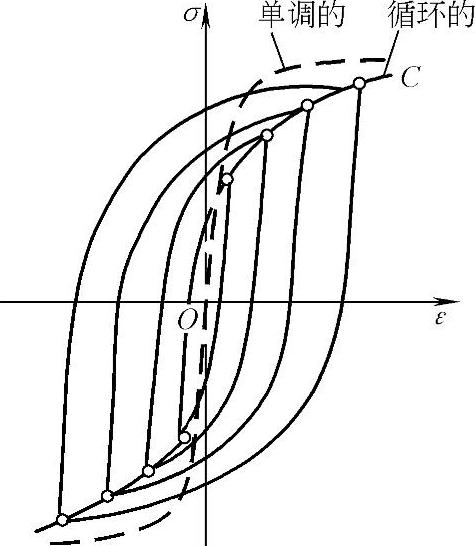
图6-120 循环应力应变曲线
循环应力应变曲线可以高于或低于单调加载的应力应变曲线。高于单调加载的应力应变曲线称为循环硬化,反之称为循环软化。
循环应力应变曲线也可用如下形式的公式表示,即
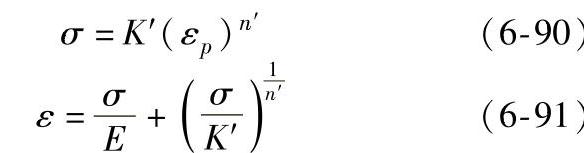
式中 σ——正应力(MPa);
εp——塑性应变;
K′——循环强度系数(MPa);
n′——循环应变硬化指数,n′=0.10~0.20;
ε——正应变,总应变;
E——模性模量。
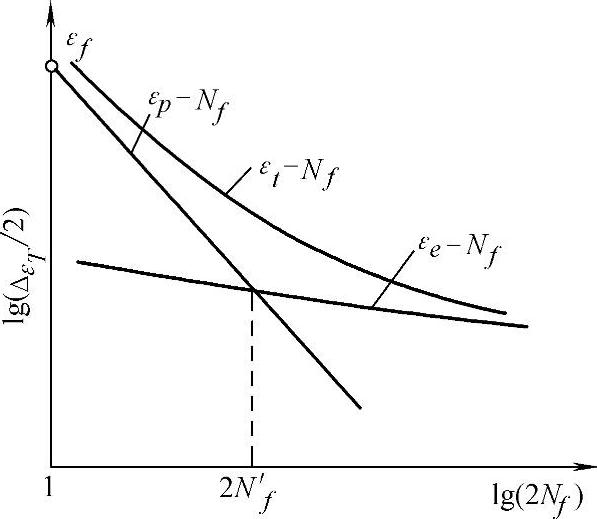
图6-121 低周疲劳应变幅-寿命曲线
在低周疲劳试验研究中,常把应变选为控制变量,建立应变范围Δεt和循环断裂周次Nf之间的曲线,叫做“应变-寿命”曲线。考虑到一个循环中包括载荷的两次“反向”,故低周疲劳中常把总寿命记为2Nf,2Nf即反向数。典型的应变幅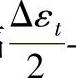 循环断裂反向次数2Nf曲线绘成双对数形式,如图6-121所示。
循环断裂反向次数2Nf曲线绘成双对数形式,如图6-121所示。
应变幅Δεt可分为弹性部分Δεe和塑性部分Δεp,整个曲线又可分解为 两条直线,其数学表达式分别为
两条直线,其数学表达式分别为
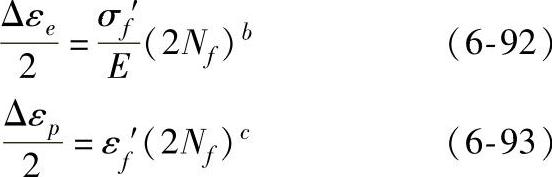
式中 σf′——疲劳强度系数,与静拉伸正断裂应力σf接近,可近似地认为σf′=σf;
b——疲劳强度指数,对软金属其绝对值不超过0.12,随强度增高,b值略有下降,最小值不低于0.05;
εf′——疲劳塑性系数,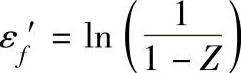 ,Z为静拉伸的断面收缩率,也可取
,Z为静拉伸的断面收缩率,也可取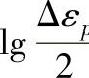 -
-
lg2Nf曲线上,2Nf=1时的应变值;
c——疲劳塑性指数,对于一般金属材料,c在0.5~0.7之间,一般可取0.6。
工程上常假定对所有材料Δεe-N和Δεp-N曲线的斜率都是共同的,得出通常所说的“通用斜率方程”为
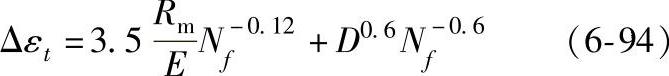
式中 D——断裂伸长率,可用静拉伸真实断裂伸长
率εf表示。
这样就可根据静拉伸性能和循环应变计算低周疲劳断裂寿命。
低周疲劳试验,要求能够有充分可调整的频率范围,可变化的加载波形,精确的应变、应力或行程的控制和测量系统,以及复杂的程序控制加载、记录和数据处理系统。近代发展起来的电液伺服疲劳试验机可以满足这些需要,使低周疲劳的试验工作得到很大推进。
表6-37所列是某些钢铁材料的单调与循环应变特性。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




