定量金相数据统计分析方法

任何一个物理量的测定不可避免地带有偏差，即测量值x与真值μ之间有一定的差值，定量金相也不例外。因此，在给出测定值时，应该同时对试验数据进行统计处理。

5.3.3.1 统计分析基础

高斯误差函数描述了测量数据的分布特点，其表达式为

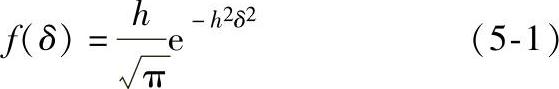
式中 δ——测量偏差值，δ=x-μ；

h——精确度指数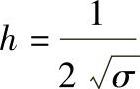，，其中σ为标准偏差。

高斯误差函数的图形像钟形（图5-19a），这种分布又称正态分布。高斯误差函数具有下述性质：

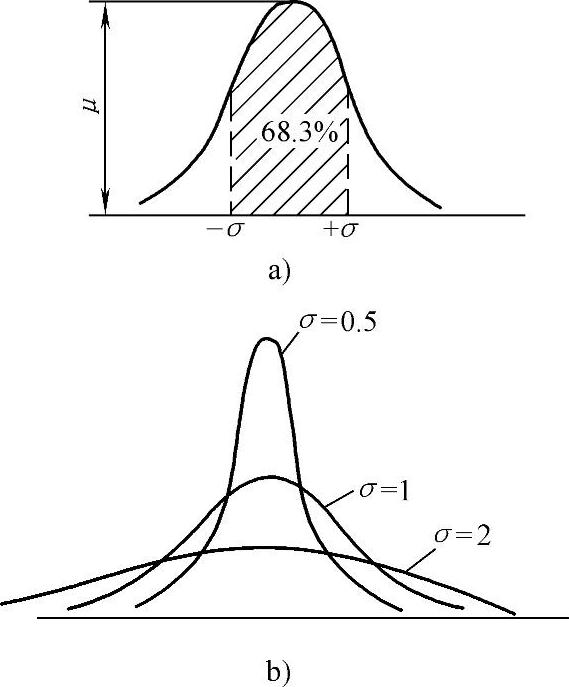
图5-19 高斯分布曲线

a）高斯分布曲线及落在拐点±σ区间内的几率

b）不同σ值下的高斯分布曲线

（1）钟形曲线所包围的面积为1，故在钟形曲线的任意区间下方的面积表示测量偏差落在该区间内的几率。由该曲线可知：出现大偏差的几率比小偏差的低，正、负偏差几率相同。

（2）曲线具有拐点，拐点的位置在±σ处。不同σ值下钟形曲线的形态如图5-19b所示。由图可见：σ大时曲线较为平坦，即数据比较分散。

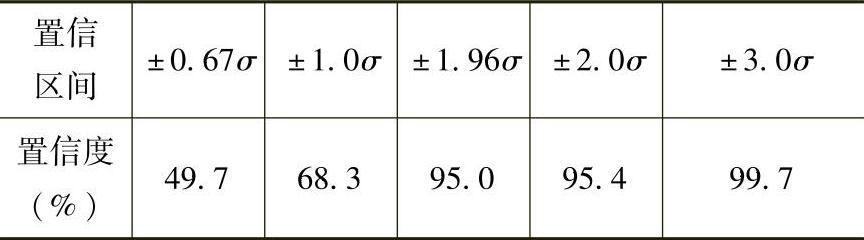
（3）测量偏差的区间（置信区间）与数据在该区间内出现的几率（置信几率，又称置信度）有确定的关系。不同测量偏差区间（置信区间）的置信度见表5-12。由该表可见：测量偏差落入±2σ区间内的几率为95.4%，即有95.4%的数据之偏差值不大于±2σ。

表5-12 不同测量偏差区间（置信区间）的置信度

5.3.3.2 数据处理

作为完整的报告，一般要给出以下数据：

1.算术平均值xx是多次测量的平均值，即(www.xing528.com)

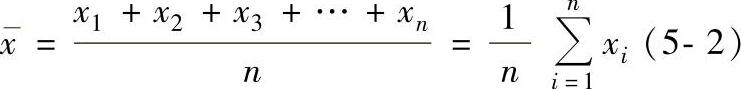
平均值仍是随机参量，当测量次数足够多时，它可以近似作为被测参量的真值。

2.标准偏差σ在有限测量次数下，标准偏差为

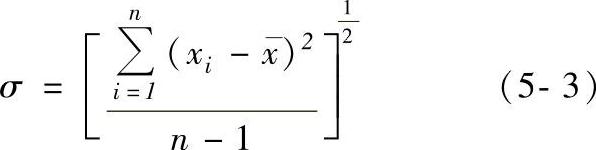
由式（5-3）可见：σ的量纲与x相同，但它并不是测量的具体误差，而是说明了数据的分散性，σ越大数据越分散。

3.离差系数（或相对标准偏差）C_V其计算公式为

C_V是无量纲量，其意义与σ相近，但反映的是测量数据波动的相对量，C_V值越小，则相对波动越小。

4.测量精确度 精度常以误差的大小表示之。绝对误差Δ是指算术平均值与真值的差，但真值并不可知。根据统计分析推导得知：绝对误差Δ与测量次数n及标准偏差σ有关，（n越大、σ越小则精度越高），同时也与人们对试验数据所要求的置信度有关。通常所要求的置信度为95%，在该置信度下测量的绝对误差约为

㊀ 不同参考书提供的计算公式不同，但结果差别不大，计算时也可采用其他公式。

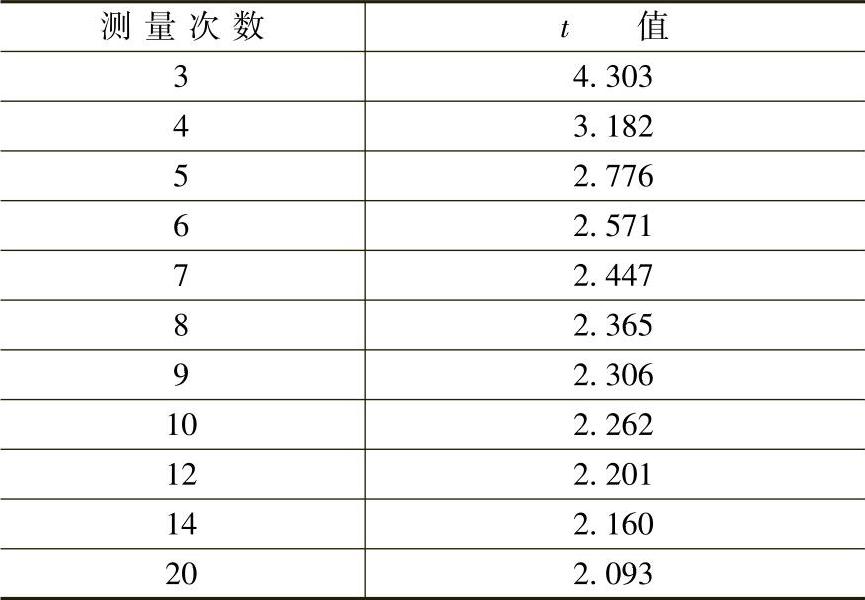
式中的t是随测量次数而变的系数（在有限次数测量时，测量次数服从t分布），t值可从表5-13中查得。

表5-13 置信度为95%时的t值

实际工作中难以根据绝对误差的值来判断两组数据的优劣，因此更多采用相对精度（或相对误差）ε来表示测量精度。

根据式（5-5）和式（5-6），可求得测量精度，反之，也可根据所要的精度确定应该测量的次数。