金属橡胶的恢复力特性分析

对于金属橡胶的大迟滞回线，分解为弹性部分和摩擦阻尼部分，将其表示为［2］

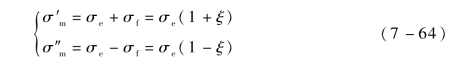
式中，σ′m为加载曲线；σ″m为卸载曲线；σe为非线性弹性力；ξ为比例常数，它与σe的乘积表示非线性摩擦阻尼力σf。

其中，非线性弹性力σe主要由螺旋卷的弹性变形产生，由式（7-63）确定；而非线性摩擦阻尼力主要由摩擦力产生，其大小与金属橡胶内部接触点数目有关。

由金属橡胶的内部结构可知，外载荷作用下金属丝螺旋卷之间的接触点分为无剪切作用力的接触点和存在摩擦作用的接触点，而存在摩擦作用的接触点又包含接触未滑移和接触滑移两类。为便于对金属橡胶内部接触点从物理本质上进行量化描述，认为金属橡胶构件内部曲梁接触角、摩擦力方向都是独立的、随机分布的，且三维空间内分布的存在接触摩擦作用的接触点数量满足泊松分布特性。将金属橡胶构件的循环加载-卸载过程看作可任意提高载荷阶段且接触点连续变化的过程［84］（图7-19），则可确定金属橡胶在加载-卸载过程中存在摩擦作用接触点数目与接触点总数目的比例关系，其中初始加载AB段为

卸载BC段为

重复加载CD段为

(www.xing528.com)

式中，λ为与接触点有关的比例系数；u的取值与加载-卸载阶段有关，加载阶段u＝1，卸载阶段u＝2。

由式（7-63）～式（7-67）确定金属橡胶加载-卸载过程的摩擦阻尼力为

式中，i＝1，2，3，分别代表初始加载段、卸载段、重复加载段曲线。

由式（7-63）和式（7-68）确定金属橡胶初始加载、卸载和重复加载过程的迟滞恢复力为

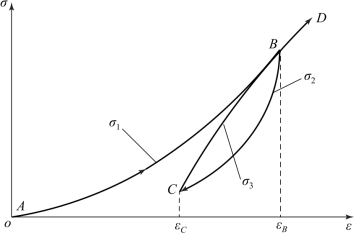
图7-19　金属橡胶的循环加卸载过程

式（7-69）即金属橡胶迟滞恢复力理论模型，可反映金属丝径d、金属丝弹性模量E、材料相对密度ρ-MR、螺旋卷直径D等基本结构参数的影响。通过该模型可以确定金属橡胶任意加载、卸载点的变形曲线，由此也就可以获得任何存在预变形的金属橡胶的变形曲线。式中，参数a、b、ξ、λ可通过最小二乘法拟合大迟滞回线的加载和卸载实验数据获得。