螺旋卷单元的变形分析

金属橡胶成型后，其内部螺旋卷的分布及排列已基本固定，在成型方向的大部分螺旋卷平面垂直于成型方向。根据成型方向螺旋卷的分布，将曲梁简化为直径为D的圆弧，在整体坐标系xyz和局部坐标系abn中建立的曲梁受力模型如图7-16（a）所示。曲梁位于ab平面内，与z轴的夹角为α，其中A点固定，B点受到沿n方向的接触作用力Fn。

取垂直于曲梁的截面C［图7-16（b）］，这时截面弯矩和扭矩分别为

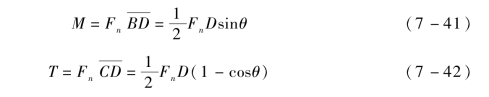
由卡氏定理得到曲梁n方向的变形为

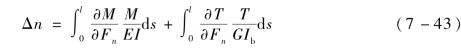
式中，ds＝Ddθ／2，θ（0＜θ＜2π）为极角；E、G、υ分别为金属丝的弹性模量、剪切模量和泊松比，且G＝E／（2+2υ）；I、Ib分别为金属丝截面惯性矩和极惯性矩，其中I＝πd4／64，Ib＝πd4／32。

将上述各参数代入式（7-43），积分得

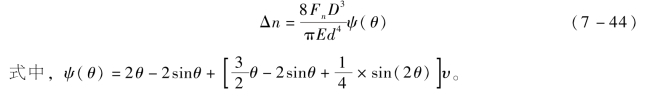
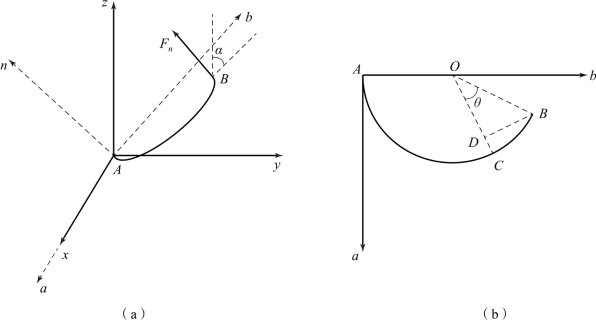
图7-16　成型方向曲梁受力模型

（a）受力图；（b）ab平面

则曲梁n方向的刚度为

对ψ（θ）求解拟合，将其进一步简化为

式中，λ和δ为常数，其取值与υ有关。

由于曲梁的长度较短，一般小于0.8圈［61］，δ的影响较小，将其忽略。将式（7-46）代入式（7-45），曲梁刚度近似为

根据萨依莫勒达诺模型［2］，在接触点处建立曲梁AB的接触作用模型，如图7-17所示。模型中将曲梁AB简化为悬臂直梁，直梁长度为曲梁两端的距离，其刚度和夹角α均与曲梁相同，与其接触作用的另一曲梁简化为平行于载荷z方向的刚性杆BC，两者在接触点B的法向发生相互作用。则曲梁AB在z方向的弹性力为

曲梁变形后，接触点由B点移至B′点，根据BB′和BB″的位移关系得(www.xing528.com)

式中，Δz为曲梁z方向的位移。

将式（7-49）代入式（7-48）得

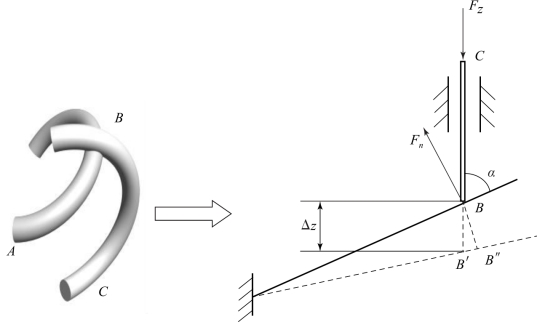
图7-17　曲梁接触作用模型

因此，曲梁z方向的等效刚度为

当极角为θ时，曲梁的长度为

由式（7-47）、式（7-51）和式（7-52）得

随着压缩变形的增加，单匝螺旋卷单元被β（β＝πD／l）个长度为l的并联曲梁代替，那么应变为ε时成型方向单匝螺旋卷的等效刚度为

在变形过程中，曲梁的长度l将随应变ε的增大而减小，且与ε呈线性关系［2］，则l可表示为

式中，l0为曲梁的原始长度；b为比例系数。

令l0＝πφD（φ为比例系数，φ＞0），将其代入式（7-55）得

将式（7-56）代入式（7-54）得