金属橡胶的非线性弹性模量模型

式中，CN为待定系数；由6.2.3节可知，nEMS为

式中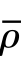，＝ρMR／ρ，ρMR为金属橡胶的密度，ρ为金属丝材料的密度。

由式（7-22）和式（7-23）可得

假设在实际材料内部，接触对均匀分布，接触对线密度为

在数值模型算例中，加载过程中最小接触对数量为331，卸载过程中最小接触对数量为367，数值模型中共有572个弹性微元。即每个弹性微元在加载、卸载时，至少分别被重复了次。因此，可以假设每个弹性微元都参与了接触对的构成，也就是假设材料内部只有滑动接触对和非滑动接触对两种基本单元，没有单独的、不参与接触对构成的弹性微元。

金属橡胶材料内部组织结构十分复杂，接触对间的串并联关系难以完全准确获取。为便于分析，用如下分层串并联模型对接触对间的串并联关系进行近似描述。取一单位立方体微元，假定在垂直于加载方向的单位面积上有m个接触对并联，其中滑动接触对ηm个，非滑动接触对（1-η）m个，在加载方向上的单位长度上有n层接触对串联，如图7-10所示。

图7-10　接触对串并联模型

在图7-10的模型中，加载时，每层的刚度为(www.xing528.com)

因为层与层串联，可得单元体在加载方向的刚度为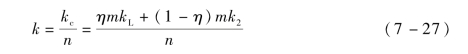

若该单位立方体微元与金属橡胶在加载方向有相同的刚度特性，则金属橡胶材料在加载方向的应力-应变关系为

设m＝C1，n＝C2ρl，则式（7-28）可写为

式中，CL为待定系数。

同理，卸载时，金属橡胶的弹性模量为

式中，CU为待定系数。

将式（7-19）、式（7-21）和式（7-25）代入式（7-29），同时，根据7.1.1节的结论，η取0.8，则式（7-29）变为

将式（7-20）、式（7-21）和式（7-25）代入式（7-30），η取0.8，则式（7-30）变为