接触对力学模型 y 向等效刚度的影响

将接触对力学模型看作一个整体，在加载或卸载时，y向的弹性变形和干摩擦作用同时发生，弹性恢复力与弹性微元的y向变形成正比，摩擦副摩擦力的大小与接触正压力成正比。因此，将滑动接触对y的力学特性用如图7-6所示的模型进行描述。

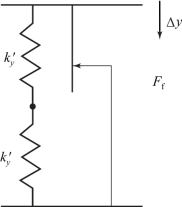
图7-6　滑动接触对y向力学模型

在图7-6所示的力学模型中，每个弹性微元的y向压缩刚度用k′y表示，由6.2.2节可知

滑动摩擦副的滑动摩擦力Ff可以用滑动摩擦模型进行计算，如图7-7所示。滑动摩擦力Ff的大小与接触正压力成正比，根据摩擦定律得

式中，kf为两弹性微元z向因接触产生的刚度；Δz为两弹性微元在接触位置的z向相对位移；μ为摩擦系数。

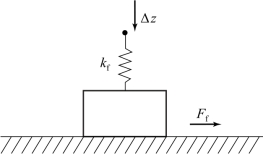
图7-7　滑动摩擦模型

在实际材料中，每个弹性微元与周边金属丝发生多处接触，这些接触使弹性微元在z向可以视为h个小曲梁并联。利用如图7-8所示的模型，对刚度kf进行计算。

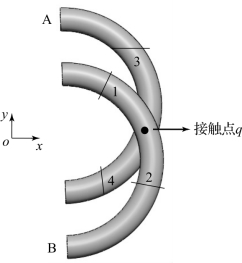
图7-8　kf计算模型

图7-8的模型中，弹性微元A与弹性微元B在q点发生接触，每个弹性微元可以视为由h个小曲梁并联，其中，弹性微元A在q点附近的小曲梁为曲梁3和曲梁4，弹性微元B在q点附近的小曲梁为曲梁1和曲梁2。由6.2.1节可知，每个小曲梁的刚度为

曲梁1和曲梁2并联，刚度为

曲梁3和曲梁4并联，刚度为(www.xing528.com)

k12与k34串联，刚度为

则加载时，接触对模型的y向力为

建立弹性微元局部坐标的方法，可以使局部坐标的x轴与全局坐标的XOY平面平行，即元件加载方向与局部坐标yoz平面平行。加载方向、局部坐标z向、局部坐标y向三者的关系如图7-9所示。若局部坐标z轴与全局坐标Z轴的夹角为φ，则

式中，ΔS为接触对模型在加载方向的变形；Δz、Δy分别为ΔS在局部坐标z向、y向的分量。

由式（7-12）和式（7-13）可得

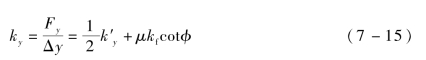
则加载时y向等效刚度为同理，卸载时y向等效刚度为

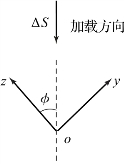
图7-9　局部坐标yoz平面

对于非滑动接触对，其y向刚度为两个k′y串联，即