确定h与ε的关系优化为：如何确定h和ε的关系？

式（6-29）中，h为应变ε的函数。h与ε的函数关系表示了弹性微元在局部坐标z向上，由接触作用变为并联曲梁的个数与应变之间的关系。当刚开始加载时，弹性微元在局部坐标z向没有发生弹性变形，即z向上并没有发生多段曲梁并联的情况，此时h＝1，对应F（h）变为

为了去除实验误差造成的数据波动，将“载荷-位移”实验数据进行多项式拟合，得到载荷-位移关系为

式中，DMR为加载量；FMR为载荷。

实验数据和拟合多项式曲线如图6-17所示。

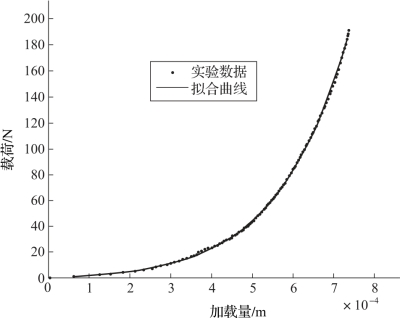
图6-17　实验数据拟合

根据拟合后的数据可得元件的刚度KMR，则实验数据对应的金属橡胶弹性模量为式中，LMR为金属橡胶元件加载方向的厚度尺寸；AMR为金属橡胶元件垂直于加载方向的截面面积。

DMR对应的加载方向应变为

“载荷-位移”数据中，设第一个数据点对应的应变为ε0，根据式（6-32）可以得到ε0对应的金属橡胶弹性模量E0。此时加载刚刚开始，F（h）近似等于F0，将E0、F0代入式（6-29）求得(www.xing528.com)

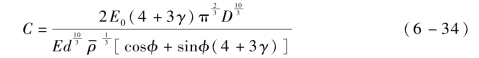
根据实验数据和式（6-33）可得每一个数据点对应的应变εi，根据实验数据和式（6-32）可得每一个数据点对应的弹性模量Ei，根据离散数据Ei、式（6-29）、式（6-34）可以得到应变为εi时对应的离散数据F（hi），求得F（hi）对应的数值解hi，最后用离散数据εi与hi作图，如图6-18中虚线所示。

可见，h与ε近似呈线性关系，因此可设

拟合h＝aε+b，如图6-18中实线所示。

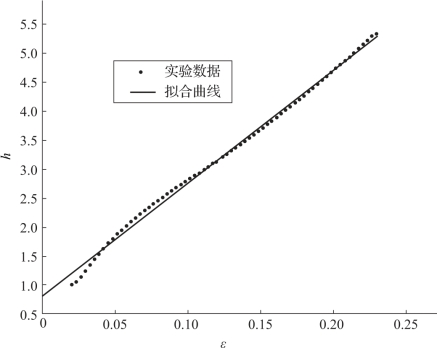
图6-18　h与ε的关系

最终，综合式（6-15）、式（6-29）、式（6-35）可得金属橡胶材料的非线性弹性模量的数学表达式：

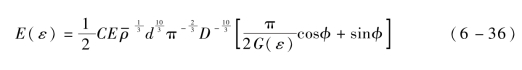
式中，

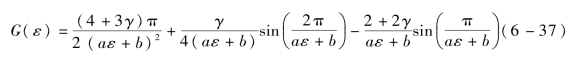
式（6-36）和式（6-37）中各项参数的物理意义分别为：C为修正系数，反映了所用力学模型与实际材料中弹性微元空间分布的差异；E为金属丝弹性模量；ρ-为相对密度，ρ-＝ρMR／ρ，ρMR为金属橡胶材料的密度，ρ为金属丝材料密度；d为金属丝直径；D为螺旋卷直径；φ为弹性微元局部坐标z轴与全局坐标Z轴夹角的均值，反映了弹性微元的空间方位信息；γ为金属丝材料的泊松比；a表示弹性微元在局部坐标z向上由接触作用变为并联曲梁的个数随应变ε增长的速率，它从细观上反映了金属橡胶刚度非线性的强弱；b表示应变为0时，弹性微元在局部坐标z向上由接触作用变为并联曲梁的个数，b的理想数值为1。