弹性微元的变形模式分析

1.弹性微元空间运动分析

截断后，金属橡胶数值模型被分解为一系列弹性微元体。分析准静态加载前后弹性微元的空间运动情况，以便对内部机理进行探索。图6-5所示为任选的一个弹性微元在加载前后空间位置的三向视图，浅色部分为加载前弹性微元的空间位置，深色部分为加载后弹性微元的空间位置。弹性微元的节点坐标位移包括平移、转动和弹性变形三部分。由图6-5可知，弹性微元的主要空间运动为空间平移。

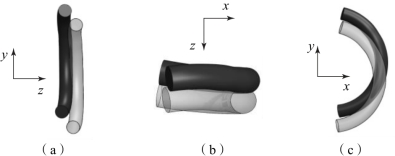
图6-5　弹性微元运动示意图

（a）左视图；（b）俯视图；（c）主视图

2.弹性微元弹性变形分析

为了进一步对弹性微元的变形情况进行研究，在节点位移中减去弹性微元的空间平移成分。弹性微元的空间平移量用其所有节点在相应方向位移的均值估算，例如x方向的位移大小为式中，d-x为弹性微元在x方向的位移；dxi为各节点在x方向的位移；n为微元上的节点数量。

在节点位移中减去x、y、z三个方向的平移成分后，弹性微元在加载前后的三向视图如图6-6所示。

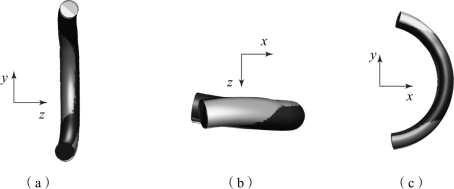
图6-6　弹性变形对比

（a）左视图；（b）俯视图；（c）主视图

图6-6中，浅色部分为加载前弹性微元的几何构型，深色部分为加载后弹性微元的几何构型，深色、浅色部分重合区域较多。由图可见，弹性微元并无明显的空间转动。由于加载量相对较小，又被分配到众多的弹性微元体上，而分配到每个弹性微元上的运动主要体现为平移运动，因此，弹性微元的空间转动很小。为简化问题，不考虑弹性微元的转动，假设减去空间平移成分后，所剩余的变形即微元体的弹性变形。

3.弹性微元z向弹性变形分析

将弹性微元的弹性变形分为局部坐标中的z向弹性变形和xoy平面内的弹性变形两方面进行分析。

首先分析z向的弹性变形，图6-6反映了弹性微元在z向和xoy平面内的弹性变形情况。为了更好地观察弹性微元在局部坐标z向的变形情况，将变形前后弹性微元各节点的z向坐标作图，如图6-7所示。图6-7中，点表示加载前微元上各节点的z向坐标，实线表示减去平移成分加载后微元的z向坐标，两条曲线的差异可以反映弹性微元在z向的弹性变形情况。由图6-7可见，弹性微元在z向上并没有整体偏向z轴正向或整体偏向z轴负向，而是两端向z轴负向发生弹性变形，中间部分向z轴正向发生弹性变形，这主要是由于该微元受到相邻微元作用的结果。

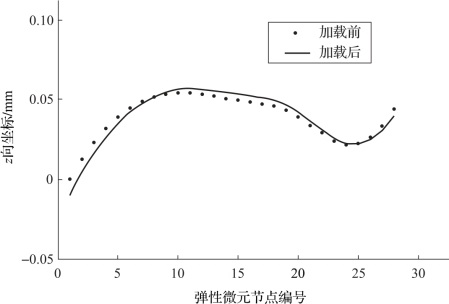(www.xing528.com)

图6-7　弹性微元节点z向坐标

图6-8表示了在准静态加载时该微元与邻近微元的相互作用，图中深色部分表示该微元，浅色部分表示其邻近微元。在局部坐标z向，随着载荷的增加，该微元向z轴负向移动，并与邻近微元发生接触作用，导致该微元发生了如图6-7所示的弹性变形。

通过上例可知，弹性微元未必整体向z轴正向或z轴负向发生弹性变形，在邻近微元的作用下，可能发生部分向z轴正向、部分向z轴负向的弹性变形。此时，弹性微元在z向上发生的弹性变形可以等效为若干尺寸更小的平面悬臂曲梁并联。如上例中，弹性微元可以在与邻近微元的接触位置打断成两个尺寸更小的平面曲梁，两个平面曲梁在z向上并联。

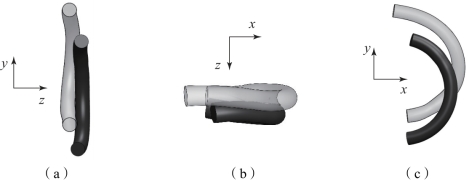
图6-8　弹性微元与邻近微元的相互作用

（a）左视图；（b）俯视图；（c）主视图

4.弹性微元xoy平面内弹性变形分析

图6-6（c）反映了微元在xoy平面内的弹性变形情况。为了更好地观察微元在xoy平面内的弹性变形，将微元轴线节点的x、y坐标作图，如图6-9所示。图6-9中，点表示变形前弹性微元的位置，实线表示变形后弹性微元的位置。由图可知，xoy平面内微元的弹性变形量很小，变形模式为：弹性微元y轴正方向的一部分向y轴负向发生弹性变形，弹性微元y轴负方向的一部分向y轴正向发生弹性变形。可见，弹性微元在xoy平面内发生了使弹性微元两端点距离变小的弯曲变形。

图6-9　弹性微元节点坐标

图6-10所示为加载后，该弹性微元的应力状态。由图可见，应力最大位置约位于弹性微元的中部，这进一步验证了这种变形模式的正确性。弹性微元在xoy平面内发生这种变形有两方面原因：一方面，对金属丝的截断方法使弹性微元的两个端点在加载方向的坐标分别为最大值和最小值，令弹性微元整体上承受了加载方向的压缩载荷；另一方面，金属橡胶由螺旋卷制备毛坯并冲压成型，这一过程使金属丝螺旋结构相互嵌入，弹性微元与邻近微元的接触位置较多地发生于其所在平面的两侧，较少地发生于微元圆弧的内外两侧，该结论可以由图6-11进行验证。

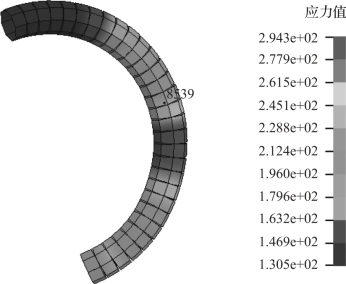
图6-10　弹性微元应力状态

图6-11所示为该微元与其邻近微元在准静态加载后的空间位置关系，深色部分表示该微元，浅色部分是该微元的相邻微元。由图可见，接触作用较多地发生在深色微元所在平面的两侧，而微元圆弧内外两侧与外界的接触作用较少，这使得xoy平面内不容易发生更加复杂的弹性变形。

图6-11　微元与邻近微元的相对位置