参数化方程简介

若基架线是一条圆柱螺旋线，方程为

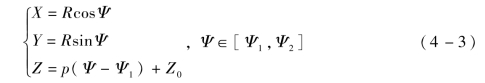
式中，Ψ为参数，［Ψ1，Ψ2］为参数Ψ的取值范围；R为基架线Γ的半径；Z0为起点z轴坐标；p为系数。

按4.1.1节的方法在基架线起点（RcosΨ1，RsinΨ1，Z0）处建立一个局部坐标系O1x1y1z1，定义为初始局部坐标系。初始局部坐标系z1轴的单位方向向量在全局坐标系下的描述为

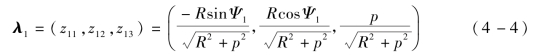
然后计算初始局部坐标系x1轴、y1轴的单位方向向量在全局坐标系下的描述。图4-2所示为向量λ1在全局坐标系下的位置示意图，λ1在XOY平面的投影λty与Y轴的夹角为α，先将λ1绕Z轴旋转α到YOZ平面内，λ1变为λ′1，λ′1与Z轴的夹角为β，再将λ′1绕X轴旋转β使λ1与Z轴重合，旋转矩阵为

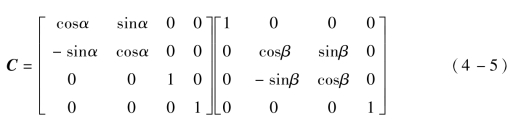
式中，α＝arccos（cosΨ1）；。

初始局部坐标系x1轴的单位方向向量（1，0，0）在全局坐标系中的描述为（x11，x12，x13），y1轴的单位方向向量（0，1，0）在全局坐标系中的描述为（y11，y12，y13），分别结合式（4-5），进行坐标变换得

图4-2　向量的旋转变换

整理可得

全局坐标系原点（0，0，0）和单位方向向量（1，0，0）、（0，1，0）、（0，0，1）在初始局部坐标系下的描述分别为（u0，v0，w0）、（ux，vx，wx）、（uy，vy，wy）、（uz，vz，wz），坐标变换为

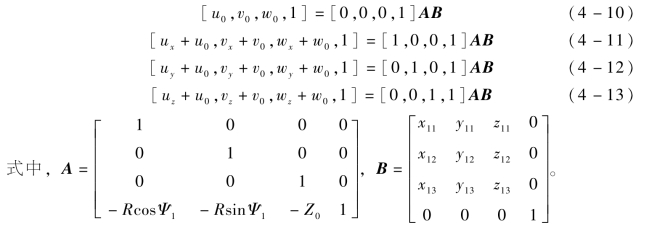
整理得

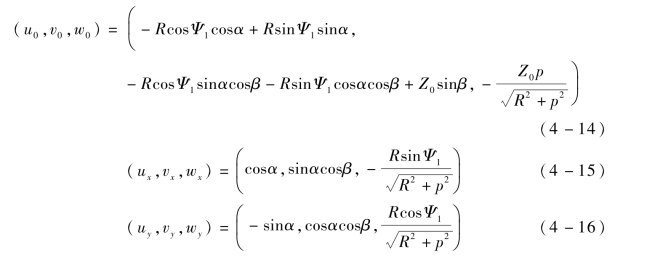
p点转动的同时，局部坐标系沿着空间曲线移动，定义移动过程中的局部坐标系为目标坐标系O2x2y2z2，如图4-3所示，λ1为z1轴的单位方向向量，λ2为z2轴的单位方向向量。

图4-3　局部坐标系几何变换

p点在局部坐标系内的转动和局部坐标系沿Γ的运动共同形成了p点的轨迹，为了计算动点p的轨迹方程，将这一过程等效为：点p始终在初始局部坐标系内转动，将初始局部坐标系O1x1y1z1通过几何变换变成目标局部坐标系O2x2y2z2，从而得到点p的全局坐标。

根据式（4-3）和曲线积分，曲线Γ的总长度为

若空间弯曲螺旋线的螺数为n，每个螺数对应的基架线长度为L／n。局部坐标系下p点的坐标见式（4-2），p点相位为θ时，在圆上转动了θ／2π圈。局部坐标系移动了θ／（2π）个螺数，局部坐标相应的移动距离为

(www.xing528.com)

根据曲线积分，又有

联立式（4-18）～式（4-20）可得

目标局部坐标系的原点坐标在全局坐标系的描述为（RcosΨ，RsinΨ，p（ΨΨ1）+Z0），z2轴单位方向向量的全局描述为

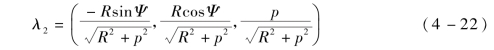
初始局部坐标系中p点坐标为（rcos（θ+θ0），rsin（θ+θ0），0），p点的全局坐标（px，py，pz）通过如下坐标变换计算：

初始局部坐标系绕向量μ旋转一定角度ζ使λ1、λ2重合，ζ为λ1、λ2的夹角，μ、ζ分别为

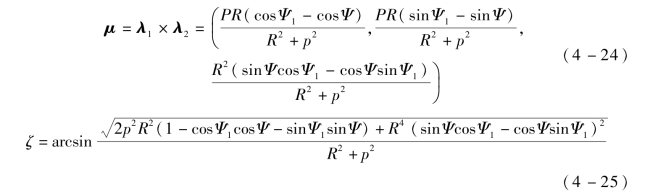
绕μ的旋转变换过程为：

（1）平移初始局部坐标系O1x1y1z1，使其原点与全局坐标系原点重合；

（2）旋转局部坐标系，使转轴向量μ与Z轴正方向同向；

（3）关于Z轴进行指定角度ζ的旋转；

（4）取（1）、（2）的逆变换将局部坐标系移至原位置，公式为［p′x，p′y，p′z，1］＝［px，py，pz，1］·

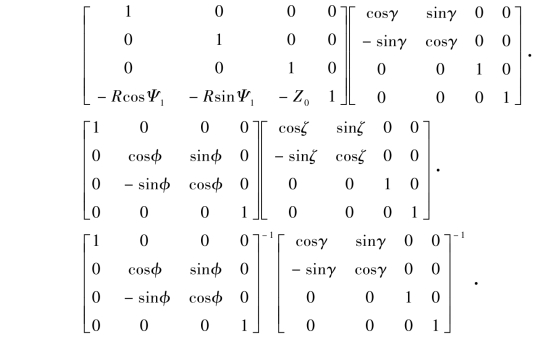
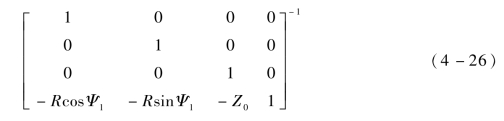
式中，γ为向量μ在XOY平面的投影与Y轴的夹角；φ为μ转动到YOZ平面后与Z轴的夹角：

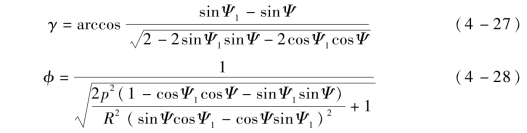
对旋转后的局部坐标系平移至目标局部坐标系，即可得到动点p的轨迹：

［p″x，p″y，p″z，1］＝［p′x，p′y，p′z，1］·

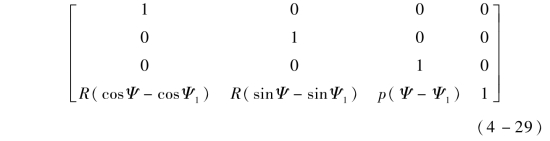
联立式（4-23）、式（4-26）、式（4-29）有

最终得到以θ为参数的p点全局参数化方程（p″x，p″y，p″z）。根据上述方法计算的某条以螺旋线为基架线的空间曲线如图4-4所示。

图4-4　空间弯曲螺旋线