路径规划实例分析

1.优化结果

根据定位销优化设计结果，对复杂构型金属橡胶毛坯铺设进行路径规划。优化计算中，交叉概率取0.8，变异概率取0.1，竞赛规模取3，定位销直径取4 mm，螺旋卷直径取3.6 mm，评价因子阈值取0.1。

每一层铺设路径取14条时，前10层路径规划如表2-3所示。第1层起点定义为编号15的定位销，其余每层的起点为上一层的终点。随着铺设层数的增加，铺设底面背景网格中权值为零的网格数量所占比例（目标函数a）逐渐减小，铺设到一定层数时，螺旋卷将整个铺设区域铺满。目标函数b用于评价毛坯的平面组织均匀性，由于每条螺旋卷只能覆盖一部分背景网格，且螺旋卷必须在定位销上缠绕，使被缠绕的定位销附近材料更多，相应的底面背景网格权值也更大，因此目标函数b的值越来越大。目标函数c用于评价毛坯的空间组织均匀性，在单层背景网格中，所选定的路径长度使铺设路径所覆盖的背景网格数量少于没有被覆盖的背景网格数量，被覆盖的网格权值大于零，没有被覆盖的网格权值为零，因此随着铺设层数的增加，权值为零的网格在所有单层背景网格中所占比例变大，使目标函数c和空间网格权值均值总体存在微小的下降趋势；并且不同铺设层之间，螺旋卷所占的空间大小略有不同，因此目标函数c和空间网格权值均值在下降时略有波动。随着铺设层数的增加，螺旋卷之间的交叉重叠面积越来越多，交叉重叠面积比螺旋卷总投影面积的增加速度要快，因此目标函数d逐渐减小。随着铺设层数的增加，材料变多，平面网格均值变大。

表2-3　铺设路径

适应度函数的值由4个目标函数的值加权求和，由于主要考虑材料的均匀性，兼顾螺旋卷的接触状态，且目标函数a和目标函数c的值变化较小，因此适应度函数与目标函数b的变化趋势一致。在各层铺设中，评价因子都小于所设定的阈值，表明设定的编码长度是合理的。

虽然目标函数b和适应度函数的数值随铺设层数的增加越来越大，但是每一层解的适应度都是本层的最小值（或近似解），每一层的铺设路径都是既使铺设区域尽快铺满，又使平面均匀度和空间均匀度最好（或近似最好）的解，并兼顾了螺旋卷之间的接触状态。

2.经验铺设与优化铺设对比

图2-28（a）、（b）分别为依据经验和优化路径对毛坯进行铺设后的结果，共铺设10层。

图2-28　铺设毛坯

（a）经验铺设；（b）优化路径铺设

为了方便比较，使用背景网格对两种毛坯进行评价。两种毛坯的组织均匀性指标如图2-29所示。由图2-29可知，两种铺设方法中目标函数a、c差别不大，表明两种毛坯都将铺设区域铺满，并且空间均匀度相近。然而随着铺设层数的增加，目标函数b的差距越来越大。在第10层时，优化路径铺设目标函数b的值比经验铺设小54%，并随着铺设层数的增加差距继续增大。可见，路径规划的作用是明显的。

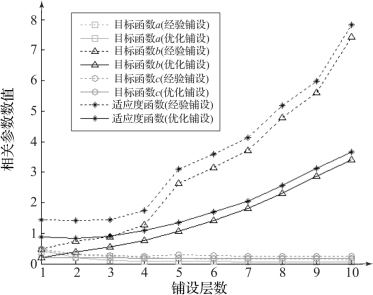
图2-29　均匀性对比

图2-30所示为两种毛坯目标函数d的比较，在刚开始铺设时，优化铺设目标函数d的值较小，但是随着铺设层数的增加，优化铺设目标函数d的值一直比经验铺设大。这是因为在路径规划中，毛坯组织均匀性和螺旋卷重叠面积之间不可能同时达到最优。故主要以均匀性为优化目标，兼顾螺旋卷的接触状态。随着铺设层数的增加，毛坯逐渐变得均匀厚实，无论采用哪种铺设方式，目标函数d的值都呈减小的趋势，且曲线斜率逐渐趋近于零，表明随着铺设层数的增加，不同的路径选择对目标函数d的影响越来越小。而实际铺设时，铺设层数较多，因此以均匀性为主要优化目标是合理的。

(www.xing528.com)

图2-30　毛坯接触状态对比

3.单层路径数对均匀性的影响

螺旋卷总铺设长度相同时，若单层路径数不同，则铺设层数不同，单层背景网格的网格总数也不同，但底面背景网格始终不变，因此选择底面背景网格分析单层路径数对毛坯组织均匀性的影响。图2-31所示为螺旋卷铺设长度相同、单层路径数不同时，毛坯的平面均匀度对比。可以看出，不同单层路径数时，底面网格方差基本不变。在铺设长度相等的前提下，单层路径数对毛坯的组织均匀性影响不大。这是因为将每层路径相连可以构成一条总路径，不论单层路径数取多少，每层的路径都是当前层最优的，组合成总路径也是使毛坯趋近最均匀的。因此，优化后，单层路径数对毛坯的铺设质量影响不大。

图2-31　单层路径数对均匀性的影响

4.单层路径数对螺旋卷接触状态的影响

图2-32所示为螺旋卷铺设长度相同、单层路径数不同时，毛坯的接触状态对比。

可以看出，随着铺设长度的增加，不同单层路径数的毛坯接触状态趋于一致。这是因为在铺设长度较短时，螺旋卷之间的交叉重叠区域较少，路径的选择对螺旋卷相互重叠面积影响较大；当铺设到一定长度时，毛坯变得均匀厚实，螺旋卷之间的交叉重叠面积急剧增大，并且受路径选择的影响越来越小。此结论与图2-30体现的结论是一致的。

图2-32　单层路径数对螺旋卷接触状态的影响

5.单层路径数对评价因子的影响

复杂构型金属橡胶算例中，定位销共19个，单层路径数最大可为18条。表2-4所示为铺设第1层时，不同单层路径数对评价因子的影响。由表2-4可见，评价因子在单层路径数较小时基本为零，单层路径数达到16时开始增大，单层路径数为18时，超过了设定阈值。

表2-4　单层路数对评价因子的影响

表2-5所示为单层路径数为18时，式（2-9）中各参数的数值。由表2-5可见，当单层路径数达到最大值18时，失败编码次数明显变多，编码失败率达31.5%；对于本节的算例，交叉操作没有受到太大影响，始终能够成功进行交叉操作；由于单层路径数取最大值时，所有定位销都在单层路径中，没有多余的定位销供变异取值，导致无法进行变异操作。

表2-5　评价因子各参数数值