遗传算法在实际中的应用

1.目标函数

定位销优化设计和路径规划的目标函数与简单构型的优化设计问题相同，详见2.4.2节。

2.评价因子

对于复杂构型金属橡胶，由于铺设区域存在孔洞或者内凹的外边界，使得在路径规划中，存在不可行路径（图2-7）。因此，针对复杂构型金属橡胶毛坯铺设路径规划问题，引入评价因子ξ，对遗传算法迭代过程进行评价，评价因子ξ为

式中，N1为总编码次数，n1为失败编码次数；N2为总交叉次数，n2为失败交叉次数；N3为总变异次数，n3为失败变异次数。

种群迭代一次，式（2-9）中各参数随之更新一次，评价因子亦更新一次。设定阈值ξ0，若评价因子ξ的值大于阈值ξ0，则表明编码、交叉、变异过程中的失败次数较多，需减小路径长度，详见2.5.1节编码、交叉和变异算子部分。

3.编码

1）定位销优化设计编码

针对复杂构型金属橡胶定位销优化设计问题，采用二进制编码。非固定定位销可以在铺设区域内任意移动，可行解的个数为无穷多个。为了使用遗传算法进行求解，将铺设区域离散化，如图2-23所示。

图2-23　铺设区域离散化

以外轮廓内凹、无孔洞，外轮廓外凸、有孔洞，外轮廓内凹、有孔洞三种构型的铺设区域为例（图2-23），首先将铺设区域在y方向用m条等间距平行线进行分割，每条平行线与铺设区域外（内）边界相交，形成若干分割线段。

然后对每一条平行线按照如下方法进行进一步离散：若平行线只与外边界相交且只有两个交点［图2-23（a）］，则该处平行线变为一条分割线段，再将分割线段用n个点等间距分割；若平行线与内、外边界只有一个交点，如只经过多边形的顶点［图2-23（b）］，则此处的n个分割点重合；若平行线与铺设区域内、外边界的交点数大于2个，则该处平行线变为铺设区域内的多条线段［图2-23（c）］，用若干分割点分别将这些处于同一y轴坐标位置的线段进行等间距分割，使得每条线段的分割点线密度相近，且这些分割点的总数为n。这样就可以用m×n个点对铺设区域内定位销的位置进行描述。为了满足二进制编码的要求，令m＝2k，n＝2l，k和l为正整数。

每个定位销的坐标在铺设区域内离散取值，表现型为坐标（x，y），基因型为二进制编码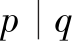。纵坐标y在铺设区域内的范围为［y1，y2］，q′为沿y正方向第q′条平行线，则纵坐标y可以表示为

假设第q′条平行线被分割成s（s≥1）条线段，沿x正方向分别是第1，2，…，s条，s条线段上的分割点数依次是n1，n2，…，ns，且

在第q′条平行线上的所有n个分割点中，p′为沿x正方向第p′个分割点，假设第p′个分割点同时也是第i条线段上ni个点中的第j个点（1≤i≤s，1≤j≤ni）。

如果s＞1，p′可以表示为

若第i条线段起点、终点横坐标分别为xi1、xi2（xi1＜xi2），则第p′个点的横坐标可以表示为

如果s＝1，则第p′个点的横坐标可以表示为

式中，x1、x2为线段起点、终点的横坐标（x1＜x2）。

如果平行线与内、外边界只有一个交点［图2-23（b）］，n个分割点重合，则每个点的横坐标都是x。

2）路径规划编码

复杂构型金属橡胶路径规划中，路径的基因型与简单构型问题相同，同样规定同一层路径不包含重复的定位销，铺设路径的起点是上一层铺设路径的终点（第1层的起点人为指定）。

对于任意一个定位销，称其他所有能和它相连构成可行路径的定位销集合为这个定位销的附属集合。在一条路径的基因型中，第1位定位销编号是上一层路径的末位编号（第1层人为指定）；在第一位定位销的附属集合内随机选择一个作为第2位；在第2位定位销的附属集合内随机选择一个作为第3位；依此类推，直至编码完成，但不允许出现重复的定位销编号。如果找不到下一位满足条件的定位销且路径没有达到设定长度，则重新编码，且式（2-9）中的n1增长一次。无论当前编码是否成功，式（2-9）中的N1都增长一次。

4.适应度函数

复杂构型金属橡胶路径规划中，适应度函数与简单构型问题相同，详见式（2-8），这里不再赘述。(www.xing528.com)

5.遗传算子

在选择、交叉、变异三种算子中，选择算子的选取与简单构型问题相同，详见2.4.2节，而交叉、变异算子需针对复杂构型金属橡胶路径规划问题进行改进。

1）交叉算子

针对定位销优化设计问题，采用均匀交叉算子。均匀交叉算子随机地产生与个体等长的0-1掩码，掩码中的数值表明了哪个父本向子个体提供变量值。

针对复杂构型金属橡胶路径规划问题，对传统的部分匹配交叉进行改进，假设两父代分别为

父代1：a b c d … e f g

父代2：h i j k … l m n

称基因中编号之间的位置为间隔点，如a与b、h与i之间各是一个间隔点。

对每一个间隔点进行判断：

（1）对于第1个间隔点：如果a与i、b与h都可以构成可行路径，则第1个间隔点是可行间隔点；

（2）对于第2个间隔点：如果b与j、i与c都可以构成可行路径，则第2个间隔点是可行间隔点；

（3）依此类推。

若一个基因型有u个编码，则有u-1个间隔点。若其中有v个间隔点是可行间隔点，则部分匹配交叉中有种可以交叉的情况，随机选择一种进行交叉。交叉后，进行匹配替换操作，改进的匹配替换方法举例如下：

假设两个父代交叉前为

父代1：a b c d … w … e f g

父代2：h i j k … b … l m n

交叉后，变为

交叉后父代1中存在重复编码b，b在匹配区域的映射编码为w，在非匹配区域中，编码b的相邻编码为a和c。如果编码a、c的附属集合都包含w，则在父代1的非匹配区域中，编码b可以被替换为w。根据匹配区域内的映射关系，对非匹配区域逐一进行替换，直至同一基因型中没有重复编码，则匹配替换操作成功。

交叉后，根据上述方法判断能否完成匹配替换操作，若不能，则随机选择其他交叉情况，直至匹配替换操作成功；若不存在成功的匹配替换操作，则交叉操作失败，进入变异阶段，同时式（2-9）中的n2增长一次。无论当前交叉操作是否成功，式（2-9）中的N2都增长一次。

2）变异算子

针对定位销优化问题，采用二进制变异算子，即随机地对基因型中的变量进行翻转。

针对复杂构型金属橡胶路径规划问题，对点位变异算子进行合理改进。传统的点位变异是对随机选择的基因型位置做值的变异。路径规划问题中，变异后的值与基因型中其他位置的编码不能相同，以保证同一层最多在同一定位销上缠绕一次。

假设某一要变异的基因型为

a b c d … e f g

首先判断基因型中每一个编码能否成为变异位置。

（1）对于首位编码a：路径的第1位定位销编号为上层路径末位定位销编号（第1层人为指定），不能作为变异位置。

（2）对于除首、末两个编码外的中间位置编码，以b为例：b的相邻编码为a和c，假设a的附属集合与c的附属集合的交集为B1，若B1包含了该基因型中的定位销编号，则将这些编号从B1中去除，所剩集合为B2。若B2不是空集，则b可以成为变异位置，B2称为b位置的变异选择集合。

（3）对于末位编码g：g的相邻编码为f，假设f的附属集合为G1，若G1包含了该基因型中的定位销编号，则将这些编号从G1中去除，所剩集合为G2。若G2不是空集，则g可以成为变异位置，G2称为g位置的变异选择集合。

判断后，在可以变异的位置中随机选择一个做值的改变，变异值在相应位置的变异选择集合中随机选取。按照上述方法，如果不能完成变异操作，那么直接将该基因型复制到下一代种群，该次变异失败，式（2-9）中的n3增长一次。无论当前变异操作是否成功，式（2-9）中的N3都增长一次。

6.精英策略

与简单构型金属橡胶毛坯铺设问题相似，为了防止种群中的最优个体因为选择、交叉、变异带来的偶然因素而丢失，遗传算法中采用精英保留策略。