遗传算法在实践中的应用

金属橡胶毛坯铺设首先要研究定位销的优化设计，路径规划是以定位销优化设计为基础的。金属橡胶毛坯铺设的定位销优化设计和路径规划问题属于组合优化问题。

在铺设工艺中，铺设区域的形状是由所制备的金属橡胶制品外形决定的。例如，对于多边形金属橡胶，顶点处必须设置定位销，称这样的定位销为固定定位销。固定定位销数量较少，还需要在铺设区域内以及边线上设置定位销，称这样的定位销为非固定定位销，如图2-10所示。对于圆形、椭圆形铺设区域，则只有非固定定位销，如图2-11所示。非固定定位销的数量、位置需要进行优化设计。

图2-10　多边形铺设区域

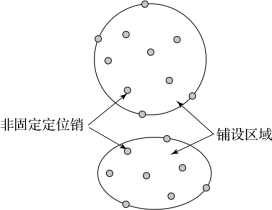
图2-11　圆形、椭圆形铺设区域

1.目标函数

1）定位销优化设计

定位销本身具有一定的直径，会侵占一定的铺设区域面积，使螺旋卷的铺设区域减小。制备工艺中，应当使用尽量少的定位销，使螺旋卷能够铺满铺设区域。根据建立的背景网格优化模型，将所有定位销（包括固定定位销）进行两两连线，找出所有可能的铺设路径，赋予连线宽度为螺旋卷直径，将所有连线向底面背景网格进行投影，统计背景网格权值，将背景网格中的非零网格数量定为目标函数。此目标函数表示了当前的定位销数量和位置所能够铺满铺设区域的能力。

2）路径规划

根据优化设计模型，以毛坯组织均匀性及螺旋卷接触状态为目标，定义目标函数。

目标函数a：铺设底面背景网格中，权值为零的网格数量所占比例，即

式中，Fa为目标函数a的值；nzero为铺设底面背景网格中权值为零的网格数量；ndm为铺设底面背景网格总数。

目标函数b：铺设底面背景网格中，所有网格权值的方差，即

式中，Fb为目标函数b的值；ndm为铺设底面背景网格总数；qi为铺设底面背景网格中各网格权值；为铺设底面背景网格中所有网格权值的均值。

目标函数c：所有单层背景网格的网格权值的方差，即

式中，Fc为目标函数c的值；nall为所有单层背景网格总数；pi为所有单层背景网格中各网格权值；p-为所有单层背景网格的权值均值。

目标函数d：螺旋卷总投影面积与螺旋卷投影之间的重叠面积总和的比值，即

式中，Fd为目标函数d的值；Sty为螺旋卷总投影面积；Sall为螺旋卷投影之间的重叠面积总和。

其中，目标函数a用于评价铺设区域被铺满的速度；目标函数b用于评价毛坯的平面组织均匀性；目标函数c用于评价毛坯的空间组织均匀性；目标函数d用于评价毛坯中螺旋卷接触状态。制备工艺多用于制备较薄的金属橡胶制品，因此平面组织均匀性是要考虑的重要特性。

金属橡胶内部线匝的接触状态很大程度上反映了材料的干摩擦耗能特性，可以通过路径规划预估毛坯中螺旋卷的接触状态，从而达到间接预估冲压成型后材料接触状态及耗能特性的目的。毛坯铺设时，螺旋卷之间在水平面内会有一定程度的交叉重叠，如图2-12所示。目标函数d越小，表明螺旋卷之间的交叉重叠区域越大，螺旋卷接触状态越好。

图2-12　螺旋卷交叉重叠

若已经铺设了k层螺旋卷（k＝0，1，2，…），则已知前k层对应的所有网格权值和第k+1层的铺设起点。利用遗传算法对第k+1层的nk+1条路径进行计算，使前k+1层对应的4个目标函数值最小。第1层的起点人为指定，最终实现铺设轨迹的优化设计。

2.编码

遗传算法不能直接处理解空间的数据，必须通过编码将它们表示成遗传空间的基因型串结构。编码应具备完备性、健壮性、非冗余性等特点。常用的编码方式有二进制编码、浮点数编码和符号编码等。

1）定位销优化设计(www.xing528.com)

针对定位销优化设计问题，采用二进制编码。非固定定位销可以在铺设区域范围内任意移动，可行解的个数为无穷多个。为了使用遗传算法进行求解，将铺设区域离散化，如图2-13所示。

图2-13　铺设区域离散化

图2-13中以五边形和椭圆形为例，首先对铺设区域在y方向用m条等间距线段进行分割，每条分割线段与铺设区域边线相交，若被分割的位置恰好是多边形的顶点或分割线与边缘相切，则此位置的分割线段退化成一个点；然后再将每条线段用n个点等间距分割，若被分割的位置是多边形的顶点或分割线与边缘相切，则此位置的n个点重合，这样就可以用m×n个点对铺设区域内定位销的位置进行描述。为了满足二进制编码的需求，令m＝2k，n＝2l，k和l为正整数。

每个定位销的坐标在铺设区域内离散取值，表现型为坐标（x，y），基因型为二进制编码。纵坐标y在铺设区域内的范围为［y1，y2］，q′为沿y正方向第q′条分割线段，则纵坐标y可以表示为

第q′条线段的起点、终点横坐标分别为x1、x2（x1≤x2），p′为第q′条线段上沿x正方向第p′个分割点，则横坐标x可以表示为

2）路径规划

针对路径规划问题，采用符号编码。将钉板上的定位销从1开始取正整数进行编号，基因型采用路径表示，基因型的长度小于或等于定位销总数。例如一条路径：

5-6-1-2-8-9-11-12-7

则基因型为

5 6 1 2 8 9 11 12 7

在铺设工艺中，螺旋卷按层进行铺设。在同一层中，如果螺旋卷在同一定位销缠绕多次，则此处的材料密度必然远大于其余位置，并且会增加很多无意义的解，使搜索空间急剧扩大，因此规定同一层路径不包含重复的定位销。铺设路径的起点是上一层铺设路径的终点（第1层的起点人为指定），因此同一层的铺设路径中，基因型中的首个编号总是相同的。

3.适应度函数

定位销优化设计中，直接选取目标函数作为适应度函数。在路径规划中，对目标函数a、b、c、d加权求和，得到统一的适应度函数，对求解过程中各路径的优劣进行评判。适应度函数为

式中，Fa为目标函数a的值，α为Fa的权重；Fb为目标函数b的值，β为Fb的权重；Fc为目标函数c的值，γ为Fc的权重；Fd为目标函数d的值，ζ为Fd的权重；F为适应度函数的值，适应度F越小，4个目标函数越优。

4.遗传算子

遗传算法一般包括选择、交叉和变异三种算子，它们构成了遗传算法强大的搜索能力，模拟的是自然选择过程中的优胜劣汰、繁殖和突变现象。

1）选择算子

常用的选择操作有轮盘赌选择、排序选择、随机遍历抽样选择、锦标赛选择等。针对定位销优化设计和路径规划问题，采用锦标赛选择，根据种群中个体的适应度进行选择操作。随机地从种群中挑选一定数目的个体，再将其中最好的个体选作父本，重复这个过程直到完成个体的选择。表2-1所示为竞赛规模与选择强度之间的关系。

表2-1　竞赛规模与选择强度之间的关系

2）交叉算子

常用的交叉操作有均匀交叉、顺序交叉、循环交叉和部分匹配交叉等。针对定位销优化设计问题，采用均匀交叉。均匀交叉随机地产生与个体等长的0-1掩码，掩码中的片段表明了哪个父个体向子个体提供变量值。针对路径规划问题，采用部分匹配交叉作为交叉算子。部分匹配交叉定义两个随机选择的交叉点之间的区域为匹配区域，交换两个父代的匹配区域，并根据匹配区域内的映射关系，对非匹配区域逐一进行交换，以产生子代铺设路径。

3）变异算子

常用的变异操作有二进制变异、逆转变异、对换变异和点位变异等。针对定位销优化设计问题，采用二进制变异，即随机对基因型中的变量进行翻转。针对路径规划问题，采用点位变异，即对随机选择的基因型位置做值的变异。对于金属橡胶毛坯铺设路径规划问题，变异值与基因型中其他位置的数字不同，以保证同一层最多在同一定位销上缠绕一次。

5.精英策略

普通遗传算法在进化过程中，种群的最优个体可能因为选择、交叉、变异带来的偶然因素而丢失，为了防止这种情况，采用能够使遗传算法依概率收敛于全局最优解的精英保留（Elitist Preservation）策略。该策略的思想是，把群体在进化过程中迄今出现的最好个体（精英个体）不进行交叉、变异而直接复制到下一代中。为了保持群体的规模不变，可以将新一代群体中最差的个体淘汰掉。