深入理解卷积与傅里叶变换

1.卷积运算概念

（1）卷积定义 卷积是数学上定义的一种运算，也被称为组合乘积、叠加积分等。一般地，对两个连续函数f（x）和h（x），采用符号“*”表示卷积运算。其定义为

z为积分变量。

z为积分变量。

（2）卷积过程 从卷积的定义式可见，卷积得到的新函数在某点x的值，是对该x求出f（z）与h（x-z）之积，然后把这些乘积对变量z从-到积分。积分过程实际是求这时二卷积函数重合区的面积。图C-16给出了卷积的几何意义。

按图C-16卷积过程的几何意义是

1）先将h（z）关于原点x=0折叠，得到h（-z）；

2）然后将h（-z）平移x₀，得到h[-（z-x₀）]=h（x₀-z）；

3）将f（z）与h（x₀-z）相乘；

（2）卷积过程 从卷积的定义式可见，卷积得到的新函数在某点x的值，是对该x求出f（z）与h（x-z）之积，然后把这些乘积对变量z从-到积分。积分过程实际是求这时二卷积函数重合区的面积。图C-16给出了卷积的几何意义。

按图C-16卷积过程的几何意义是

1）先将h（z）关于原点x=0折叠，得到h（-z）；

2）然后将h（-z）平移x₀，得到h[-（z-x₀）]=h（x₀-z）；

3）将f（z）与h（x₀-z）相乘；

图C-16 卷积的几何意义

a）二个卷积函数 b）g（0）值（图中阴影区面积） c）g（1）值（图中阴影区面积） d）g（2）值（图中阴影区面积） e）g（5）值（图中阴影区面积） f）g（6）值（无重合区，为0） g）卷积函数g（x）值

图C-16 卷积的几何意义

a）二个卷积函数 b）g（0）值（图中阴影区面积） c）g（1）值（图中阴影区面积） d）g（2）值（图中阴影区面积） e）g（5）值（图中阴影区面积） f）g（6）值（无重合区，为0） g）卷积函数g（x）值

4）f（z）与h（x₀-z）的乘积对z积分，得到（即，求二者重叠部分面积）；

4）f（z）与h（x₀-z）的乘积对z积分，得到（即，求二者重叠部分面积）；

5）改变x₀，则可一般地写（该面积是移动量x的函数）。

（3）卷积的性质与效应 卷积的基本性质包括线性性质、交换性、平移不变性、缩放性等。在我们的讨论中，直接需要的是卷积的交换性。该性质给出的是

5）改变x₀，则可一般地写（该面积是移动量x的函数）。

（3）卷积的性质与效应 卷积的基本性质包括线性性质、交换性、平移不变性、缩放性等。在我们的讨论中，直接需要的是卷积的交换性。该性质给出的是

其证明过程如下：按卷积定义有

其证明过程如下：按卷积定义有

引入新变量

β=x-α

则有

α=x-β dα=-dβ

这样可写

引入新变量

β=x-α

则有

α=x-β dα=-dβ

这样可写

关于卷积的其他性质可参阅有关文献。

卷积运算的主要效应是平滑和展宽。平滑是指：在卷积中，被卷积函数的精细结构（如尖峰等）将被圆滑，使得到的卷积函数将比被卷积函数平滑。平滑的程度与被卷积函数的具体情况相关。展宽是指，卷积得到函数的宽度近似等于被卷积函数的宽度和。图C-17显示了卷积运算的平滑和展宽作用。

关于卷积的其他性质可参阅有关文献。

卷积运算的主要效应是平滑和展宽。平滑是指：在卷积中，被卷积函数的精细结构（如尖峰等）将被圆滑，使得到的卷积函数将比被卷积函数平滑。平滑的程度与被卷积函数的具体情况相关。展宽是指，卷积得到函数的宽度近似等于被卷积函数的宽度和。图C-17显示了卷积运算的平滑和展宽作用。

图C-17 卷积运算的平滑和展宽作用

2.傅里叶变换的概念

将函数（信号、图像）从一个域变换到另外一个域（例如，从时域转换到频域），在新的域中对函数进行分析和处理，可能方便或快速获取函数的某些特性。

傅里叶变换采用正弦函数和余弦函数为基本正交函数，对函数展开，给出了信号的基频、谐波幅度与相位，展开系数具有明确的物理意义。傅里叶变换又称为频域（谱）分析方法，它可以看作是时域函数转换到频域表示的方法。

下面从傅里叶级数开始，说明傅里叶变换意义。

（1）傅里叶级数 设f（t）是周期为T的周期函数，即

f（t）=f（t+κT）κ=0，±1，±2，…

则当该函数满足一定条件时，利用正弦三角函数、余弦三角函数的正交性，它可展开为傅里叶级数

图C-17 卷积运算的平滑和展宽作用

2.傅里叶变换的概念

将函数（信号、图像）从一个域变换到另外一个域（例如，从时域转换到频域），在新的域中对函数进行分析和处理，可能方便或快速获取函数的某些特性。

傅里叶变换采用正弦函数和余弦函数为基本正交函数，对函数展开，给出了信号的基频、谐波幅度与相位，展开系数具有明确的物理意义。傅里叶变换又称为频域（谱）分析方法，它可以看作是时域函数转换到频域表示的方法。

下面从傅里叶级数开始，说明傅里叶变换意义。

（1）傅里叶级数 设f（t）是周期为T的周期函数，即

f（t）=f（t+κT）κ=0，±1，±2，…

则当该函数满足一定条件时，利用正弦三角函数、余弦三角函数的正交性，它可展开为傅里叶级数

式中Ω=2π/T，基频。

展开式中的系数（称为傅里叶系数）的计算式如下

式中Ω=2π/T，基频。

展开式中的系数（称为傅里叶系数）的计算式如下

应用欧拉公式

应用欧拉公式

并考虑到cos（-θ）=cosθ，可写

并考虑到cos（-θ）=cosθ，可写

这样，函数的傅里叶级数展开式可改写为

这样，函数的傅里叶级数展开式可改写为

记

记

则函数的傅里叶级数展开式可进一步改写为

则函数的傅里叶级数展开式可进一步改写为

傅里叶系数则为

傅里叶系数则为

将傅里叶系数F_n的表示式代入函数的傅里叶级数展开式，则函数f（t）的傅里叶级数展开式可写成

将傅里叶系数F_n的表示式代入函数的傅里叶级数展开式，则函数f（t）的傅里叶级数展开式可写成

即，一个周期函数可以展开成无限多频率为其基频倍数的复正弦信号的加权和。图C-18给出的是一周期矩形函数的波形和其频谱（对应的傅里叶级数展开式系数）。可见，对周期函数，其频谱为离散谱。频谱线的间隔与函数周期相关，周期越长，谱线越密集。谱线幅度按确定规律（Bracewell函数）变化。

即，一个周期函数可以展开成无限多频率为其基频倍数的复正弦信号的加权和。图C-18给出的是一周期矩形函数的波形和其频谱（对应的傅里叶级数展开式系数）。可见，对周期函数，其频谱为离散谱。频谱线的间隔与函数周期相关，周期越长，谱线越密集。谱线幅度按确定规律（Bracewell函数）变化。

图C-18 周期矩形函数的波形和其频谱

a）周期矩形函数 b）周期矩形函数的频谱

（2）从傅里叶级数到傅里叶变换 对于非周期函数的傅里叶级数展开，可从周期函数处理。即，改记周期函数为

图C-18 周期矩形函数的波形和其频谱

a）周期矩形函数 b）周期矩形函数的频谱

（2）从傅里叶级数到傅里叶变换 对于非周期函数的傅里叶级数展开，可从周期函数处理。即，改记周期函数为

则对非周期函数f（t）可视为是

则对非周期函数f（t）可视为是

按前面的叙述，现在可写(www.xing528.com)

按前面的叙述，现在可写

因有Ω=2π/T，上式可写成

因有Ω=2π/T，上式可写成

当T→时有

当T→时有

，即相邻二谱线间的间隔趋向无穷小；

nΩ→ω，即离散变量nΩ趋向连续变量ω；

，即相邻二谱线间的间隔趋向无穷小；

nΩ→ω，即离散变量nΩ趋向连续变量ω；

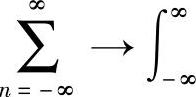
，即求和运算转变为积分。

这样，则得到

，即求和运算转变为积分。

这样，则得到

方括号中的积分部分，是参变量ω（角频率）的函数，记为F（jω），即

方括号中的积分部分，是参变量ω（角频率）的函数，记为F（jω），即

用此记号，则函数展开式又可写为

用此记号，则函数展开式又可写为

这样就给出了非周期函数的傅里叶变换。

一个函数f（t）的傅里叶变换以前常简单地记为

这样就给出了非周期函数的傅里叶变换。

一个函数f（t）的傅里叶变换以前常简单地记为

其中u为频率域变量（也可用其他符号），现在部分教材中记为

其中u为频率域变量（也可用其他符号），现在部分教材中记为

这时赋予“F[]”为对函数进行傅里叶变换运算的含意。

傅里叶变换的意义是：它说明非周期函数也可以展开为简谐函数的叠加，但不再是谐波的叠加，而是角频率连续变化的无穷多个简谐函数的叠加。即，非周期函数可以由无穷多个指数函数exp（jωt）之和表示，每个指数函数分量的大小为F（jω）。

F（jω）简单称为函数f（t）的频谱函数（实际称为频谱密度函数），也即函数f（t）的傅里叶变换。它一般为一复数，可写为

这时赋予“F[]”为对函数进行傅里叶变换运算的含意。

傅里叶变换的意义是：它说明非周期函数也可以展开为简谐函数的叠加，但不再是谐波的叠加，而是角频率连续变化的无穷多个简谐函数的叠加。即，非周期函数可以由无穷多个指数函数exp（jωt）之和表示，每个指数函数分量的大小为F（jω）。

F（jω）简单称为函数f（t）的频谱函数（实际称为频谱密度函数），也即函数f（t）的傅里叶变换。它一般为一复数，可写为

其模|F（jω）|为函数f（t）各频率分量的相对大小，幅角φ（ω）为函数f（t）各频率分量的相位。一般将|F（jω）|与ω的关系曲线称为函数信号的幅度频谱，将φ（ω）与ω的关系曲线称为函数信号的相位频谱。图C-19显示的是矩形（脉冲）函数的傅里叶变换频谱曲线。

（3）傅里叶变换卷积定理 傅里叶变换卷积定理分为两个方面：时域卷积定理、频域卷积定理。时域卷积定理给出两个函数卷积的傅里叶变换表示式，频域卷积定理给出两个函数乘积的傅里叶变换表示式。

时域卷积定理：F[f（t）*g（t）]=F[f（t）]F[g（t）]

其模|F（jω）|为函数f（t）各频率分量的相对大小，幅角φ（ω）为函数f（t）各频率分量的相位。一般将|F（jω）|与ω的关系曲线称为函数信号的幅度频谱，将φ（ω）与ω的关系曲线称为函数信号的相位频谱。图C-19显示的是矩形（脉冲）函数的傅里叶变换频谱曲线。

（3）傅里叶变换卷积定理 傅里叶变换卷积定理分为两个方面：时域卷积定理、频域卷积定理。时域卷积定理给出两个函数卷积的傅里叶变换表示式，频域卷积定理给出两个函数乘积的傅里叶变换表示式。

时域卷积定理：F[f（t）*g（t）]=F[f（t）]F[g（t）]

图C-19 矩形（脉冲）函数的傅里叶变换频谱曲线

a）门函数 b）门函数的频谱 c）门函数的幅度谱 d）门函数的相位谱

图C-19 矩形（脉冲）函数的傅里叶变换频谱曲线

a）门函数 b）门函数的频谱 c）门函数的幅度谱 d）门函数的相位谱

频域卷积定理：

下面给出两卷积定理证明（详细过程见相关文献）。

按卷积运算定义，有

频域卷积定理：

下面给出两卷积定理证明（详细过程见相关文献）。

按卷积运算定义，有

因此有

因此有

按傅里叶变换的平移（时移）性质

按傅里叶变换的平移（时移）性质

则有

则有

这样就可得到时域卷积定理结果

这样就可得到时域卷积定理结果

关于频域卷积定理可如下证明。为方便，分别记

关于频域卷积定理可如下证明。为方便，分别记

则可写

则可写

按函数f（t）与函数傅里叶变换F[f（t）]的关系，从频域卷积定理给出的结果求函数的表示式。即，对应的函数表示式应为

按函数f（t）与函数傅里叶变换F[f（t）]的关系，从频域卷积定理给出的结果求函数的表示式。即，对应的函数表示式应为

利用傅里叶变换的频移性质，可得到

利用傅里叶变换的频移性质，可得到

将其代入上面的表示式，则可写出

将其代入上面的表示式，则可写出

这样就证明了傅里叶变换频域卷积定理。

（4）傅里叶变换的另一种表示式 以上，对频域均采用了角频率变量ω给出傅里叶变换的表示式。傅里叶变换的表示式也可采用一般的频域频率变量表示。例如采用频率变量u（或v等），这时，由于两个频率变量间有关系

ω=2πu

则函数的傅里叶变换式应改写成

这样就证明了傅里叶变换频域卷积定理。

（4）傅里叶变换的另一种表示式 以上，对频域均采用了角频率变量ω给出傅里叶变换的表示式。傅里叶变换的表示式也可采用一般的频域频率变量表示。例如采用频率变量u（或v等），这时，由于两个频率变量间有关系

ω=2πu

则函数的傅里叶变换式应改写成

3.欧拉公式与证明

欧拉公式的常用表示式为

3.欧拉公式与证明

欧拉公式的常用表示式为

它给出了以e为底的复指数函数与三角函数间的关系，欧拉公式可采用泰勒展开进行证明。下面是证明的简要过程。

按泰勒级数展开三函数，得到

它给出了以e为底的复指数函数与三角函数间的关系，欧拉公式可采用泰勒展开进行证明。下面是证明的简要过程。

按泰勒级数展开三函数，得到

注意到

注意到

则立即可得到

则立即可得到