尺寸测量误差限制与像素控制

本节讨论的是要求以一定误差限制时的尺寸测量问题。

1.尺寸测量概念

对于数字射线检测技术，尺寸测量是在获得的检测图像上完成某个细节（缺陷或关注对象）的尺寸测量。这种尺寸测量，本质上是以检测图像像素尺寸为单位的测量。也就是，测量得到的尺寸，实际是细节的图像占据的像素数乘以像素尺寸得到的数值，即

D=NP

式中 D——测量得到的细节尺寸；

P——检测图像的像素尺寸；

N——在检测图像上细节图像的测量值（以像素尺寸为单位）。

为实现尺寸测量，必须确定检测图像的像素尺寸P和在检测图像上细节以像素尺寸为单位的测定值N。

由于获得的检测图像是数字图像，对细节尺寸的测量必然是以像素尺寸为单位，因此像素尺寸决定了可实现的最小测量误差，图4-20显示了这种情况。一般可认为，这时测量的最大误差将是像素尺寸的1/2。即

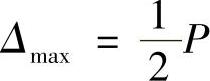
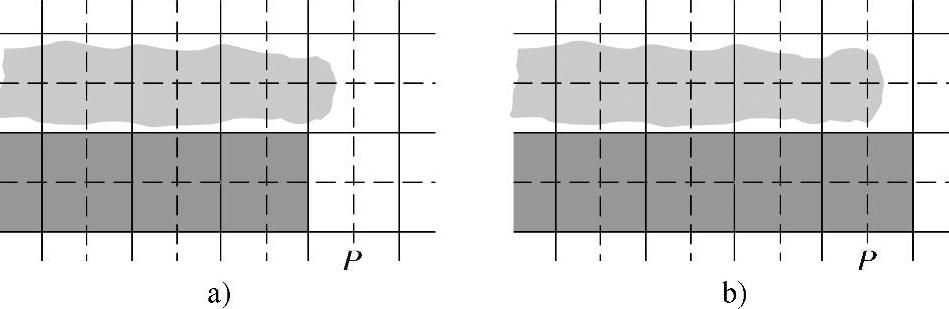
图4-20 数字图像像素尺寸引起的测量误差

为了满足细节尺寸测量误差要求，必须控制检测图像的像素尺寸，因此当要求细节尺寸测量误差为Δ时，为满足该测量误差要求，严格时应要求P≤Δ或者U_im≤2Δ。一般情况下可要求P≤2Δ或者U_im≤4Δ。

实际的测量误差还与细节图像测定值N的误差、校准确定的检测图像像素尺寸误差相关。也与采用的计算方法相关。

2.细节图像测定值N的测量方法

由于检测图像存在不清晰度（或理论上成像的卷积特性），不清晰度必然影响图像上的细节图像尺寸。图4-21显示了不清晰度对图像上细节图像尺寸的影响。概括这种影响，对于（长度较大）宽度尺寸为D的细节，当检测图像不清晰度为U_im时，可以给出细节图像宽度断面的最小宽度和最大宽度值。

1）当细节宽度尺寸不小于不清晰度时，最小宽度值为（D-U_im）；最大宽度值为（D+U_im）。

2）当细节宽度尺寸小于不清晰度时，最小宽度值为（U_im-D）；最大宽度值为（D+U_im）。

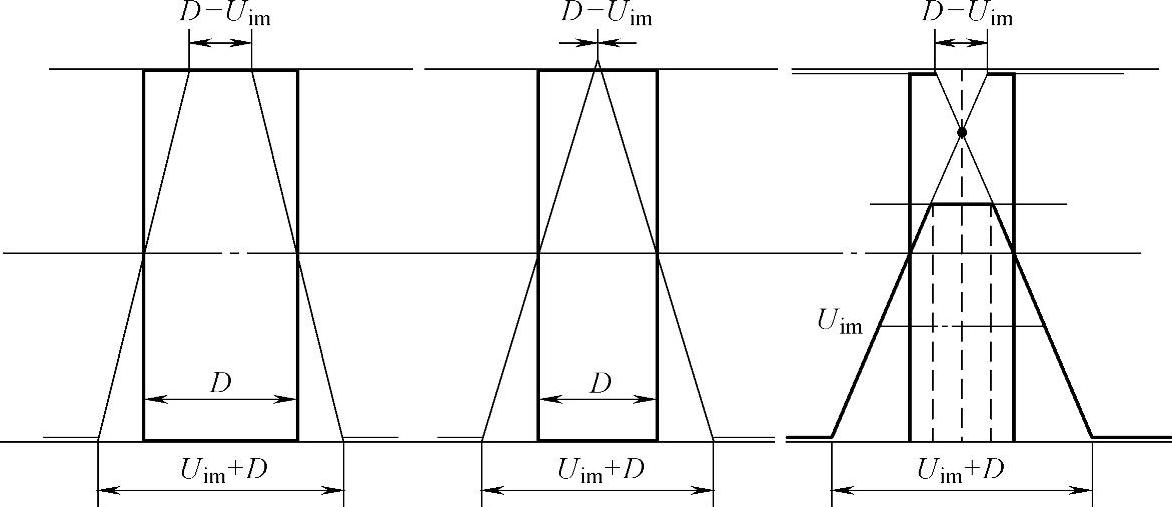
图4-21 不清晰度对图像上细节图像尺寸的影响

考虑到这种影响，在细节尺寸测量时一般采用“半高宽法”。即通过软件画出细节图像断面的幅度分布曲线，以峰值高度的1/2宽度作为测定细节尺寸的基本数据。从图4-21可以清楚看到：

1）对当细节宽度尺寸不小于不清晰度时，该数据可直接作为细节尺寸数据；

2）对当细节尺寸小于不清晰度时，该数据可作为不清晰度数据U_im，为确定细节尺寸还应测定细节图像断面的全宽度数据（U_im+D），以二者差确定细节尺寸。

实际应用这种方法处理时还应注意的是，检测图像测量值总会存在误差，因此应取多次测量值的平均值进行计算。这包括在检测图像上对细节图像、校准试块图像的测量。

3.图像像素尺寸校准确定方法

理论上检测图像的像素尺寸可按关系式

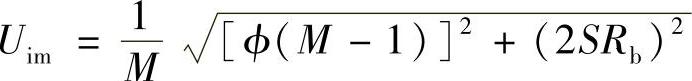
或

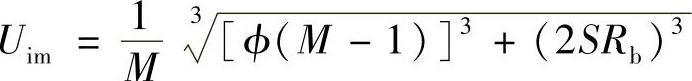
计算，但由于实际检测情况并不是理想的情况，因此在实际测量过程中一般采用校准试块确定检测图像像素尺寸。

确定检测图像像素尺寸的校准试块，一般采用与被检验材料相同的材料制作。校准试块尺寸与被检验细节尺寸接近（适当小些或适当大些），制作成适当厚度的锐利边界。一般应与被检验物体同时检验，从获得的检测图像测定校准试块尺寸对应的像素数，按下式计算校准的检测图像像素尺寸

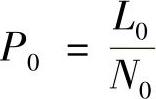
式中 L₀——标准试块尺寸；(www.xing528.com)

N₀——标准试块尺寸在检测图像上测定的像素数；

P₀——校准获得的检测图像的像素尺寸。

如果令y=L，x=N，κ=P，显然上述关系应是y=κx方程决定的直线关系。

理论上可用一点数据与坐标原点数据或用二点数据确定上面的直线方程。从此也就可给出两种校准方法：单校准试块像素尺寸校准确定方法和双校准试块像素尺寸校准确定方法。

单校准试块像素尺寸校准确定方法，是采用一块校准试块的校准像素尺寸确定方法。按上面叙述，可写

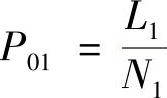
双校准试块像素尺寸校准确定方法，要采用两块校准试块，一块的尺寸小于被测细节尺寸，另一块的尺寸大于被测细节尺寸。按上面叙述，其校准获得的检测图像的像素尺寸为

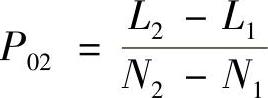
如果考虑到可能出现的误差，比较准确的是采用多个数据（多个校准试块）完成校准过程，然后用最小二乘法进行线性回归，求出校准后的检测图像像素尺寸。图4-22显示了这个情况，这时获得的检测图像像素尺寸误差会小，或说给出的直线近似与真实情况接近。

实际检测中的尺寸测量，多用单校准试块像素尺寸校准确定方法和双校准试块像素尺寸校准确定方法。

4.细节尺寸计算方法与讨论

从检测图像测定了某细节的像素值N后，其对应的细节尺寸L可按不同方法计算。

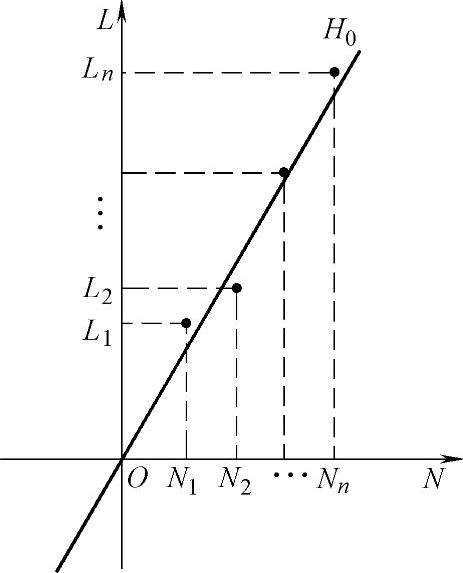
图4-22 理想的多点校准

1）校准计算方法：即采用单校准试块校准像素尺寸，按下式计算

L=NP₀₁

2）线性插入计算方法：即采用双校准试块校准像素尺寸，按下式计算

L=L₁+（N-N₁）P₀₂

或

L=L₂-（N₂-N）P₀₂

式中，下标中出现“2”的为尺寸大的校准试块的相应值。

两种校准方法引出的两种计算方法的区别在于，单校准试块的计算方法构建线性关系时，采用的是y=κx方程关系。双校准试块的计算方法构建线性关系时，一般都会是y=κx+b方程关系。由于必然存在误差，方程中的截距一般不等于0。图4-23具体显示了两种校准方法的区别及其与理想的多点校准的关系。

图中，A、B直线为单校准试块构建的线性关系，而直线H为双校准试块构建的线性关系，H₀直线为多校准试块构建的理想线性关系。

校准计算方法是按图中直线A方程（或按直线B方程）的计算方法，因此其计算结果将包含多次累计像素尺寸误差。

线性插入计算方法是按图中直线H方程的计算方法。由于两校准试块尺寸设计为适当覆盖被测量细节尺寸（一个校准试块尺寸比被测量细节尺寸小些，一个校准试块尺寸比被测量细节尺寸大些），这就决定了，在两校准试块数据点之间的测量值，与多点校准直线的偏差会小于单校准试块直线的偏差。也就是减少了测量误差。从图中，容易对此做出证明。

5.不同校准计算方法误差比较

由于获得的检测图像是数字图像，采用校准试块校准获得的像素尺寸一般都存在误差。不同校准方法的像素尺寸误差也会不同，计算结果误差也会不同。

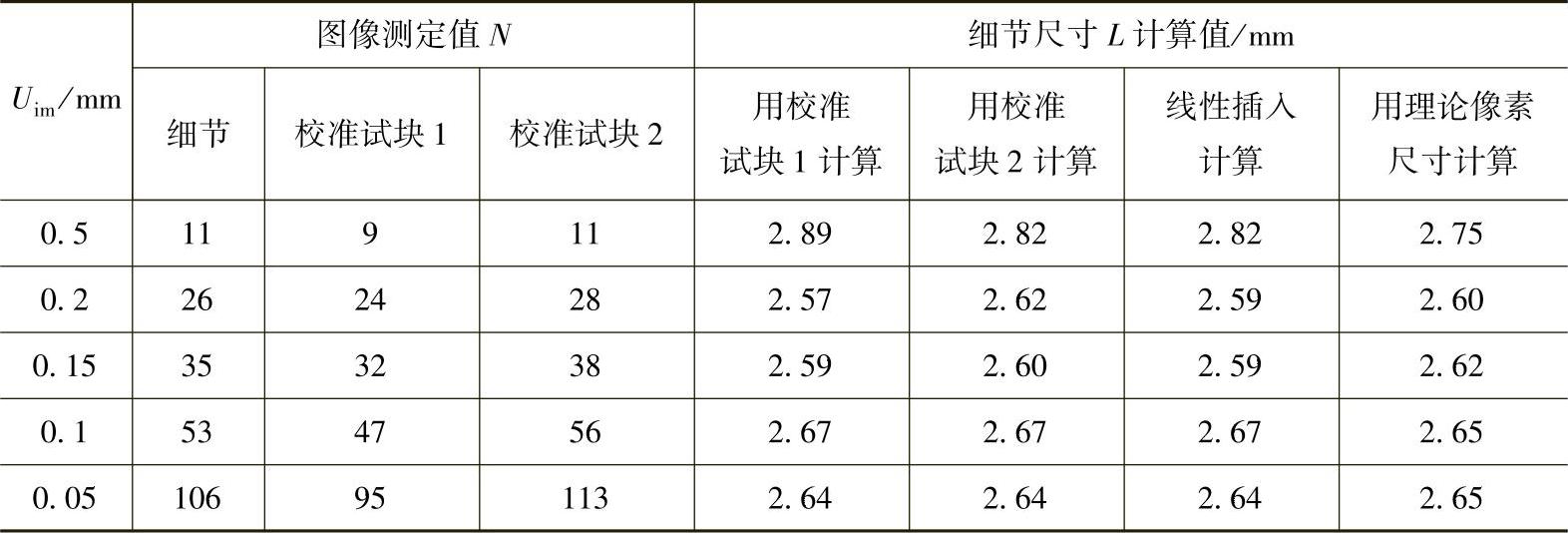
例如，细节尺寸L=2.64mm，校准试块1尺寸L₁=2.37mm，校准试块2尺寸L₂=2.82mm。表4-7给出了像素尺寸、校准方法对细节尺寸测量的影响。它显示了检测图像不清晰度、像素尺寸校准方法、计算方法对细节尺寸测量结果的影响。若测量最大误差限制为Δ=0.05mm，则从表4-7给出的结果可见，检测图像不清晰度不大于0.2mm才能满足要求。

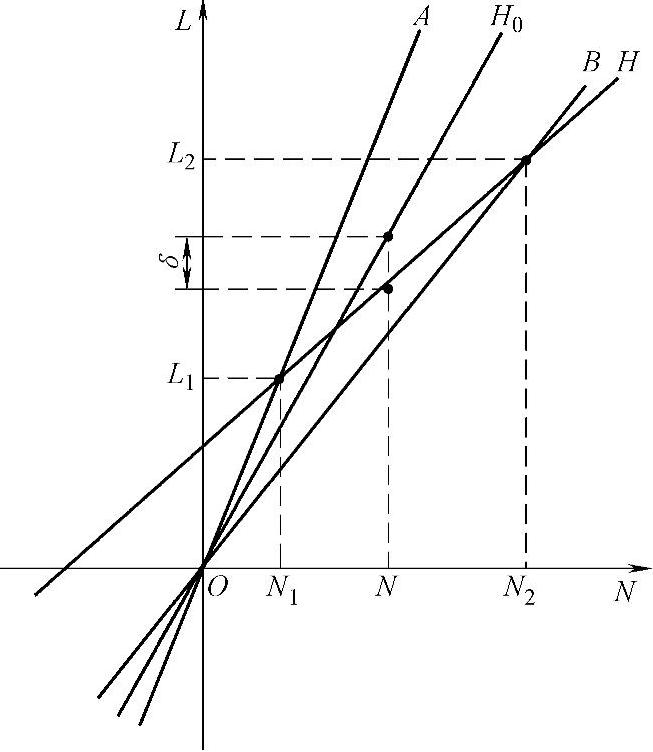
图4-23 两种校准方法的区别

表4-7 像素尺寸、校准方法对细节尺寸测量的影响（不放大的检测布置）