如何满足采样定理以准确恢复连续信号图像信息

采样过程控制的基本要求是应满足采样定理。

图3-9显示的是采用某一采样间隔对不同频率信号采样的情况。在该采样间隔下，不同的原始信号得到了相同的采样信号（见图中黑点分布）。显然，这时采样信号不能确定原始信号，或说不能正确地再现原始信号的信息。理论上，这称为出现“混叠”现象。

图像采样过程必须考虑的基本问题，是如何保证从采样得到的离散信号序列图像，能准确、唯一地恢复原来信号图像。简单理解时，可认为是如何保证抽样的离散信号序列图像不丢失、不改变原来连续信号图像的信息。

研究指出，为保证采样得到的离散信号图像能准确恢复原来连续信号图像的信息，采样间隔应足够小，需要满足的基本条件是采样频率应不小于原信号最高频率的2倍，这称为采样（取样，抽样）定理。

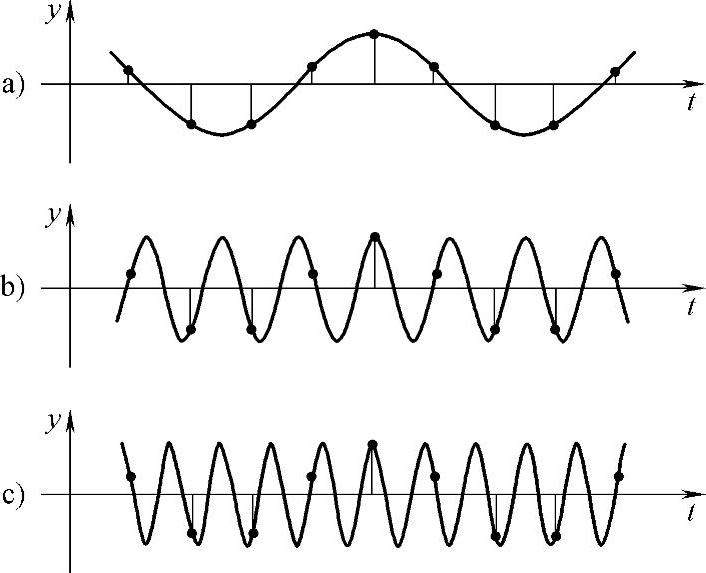
图3-9 采样间隔与混叠

对于一维图像信号f（t），如果其包含的最高空间频率为f_m，若记f_S为采样频率，则采样定理要求

f_S≥2f_m （3-1）

一般称其为奈奎斯特（Nequist）采样（取样，抽样）定理。它由奈奎斯特（Neq-uist）于1928年提出，仙农（Shannon）于1948年从理论上给出严格证明。关于采样定理的进一步理解可参阅附录B。(www.xing528.com)

对于空间采样，如果采样间隔（像素尺寸）为P_S（mm），则对应的（空间）采样频率f_S（Lp/mm）为

其单位一般为线对/毫米（Lp/mm）。如果图像的最高空间频率由尺寸为D（mm）的细节决定，则其对应的最高空间频率为

按采样定理，则容易得到

对于二维图像信号，同样需要考虑采样定理问题。这时，在两个方向（x，y方向）都需要考虑采样间隔。它们都必须满足采样定理的要求，否则会造成虚假信号，不能正确地再现原来信号的信息。