火工品力学响应仿真优化方案

在Hopkinson杆冲击针刺雷管的试验中，观测到火工品的外壳出现屈曲变形，变形特征与壳体的屈曲模态有关。研究壳体在轴向冲击载荷作用下的屈曲变形规律对于研究火工品的损伤变形规律具有重要意义。

9.3.2.1 Hopkinson压杆试验技术的原理

SHPB试验装置的机械系统由高压气枪及控制系统、撞击杆（子弹）、输入杆、试件、输出杆、吸收杆、阻尼器和装置平台等主要部件构成；测量记录系统由光电靶测速系统、贴在输入杆和输出杆中部的应变片、超动态应变仪、数据采集和分析系统，以及计算和分析软件等主要硬件和软件构成。系统中子弹、输入杆、输出杆和吸收杆为同质材料，均采用钨合金钢材料（65Si2MnWA）制成，如图9.19所示。

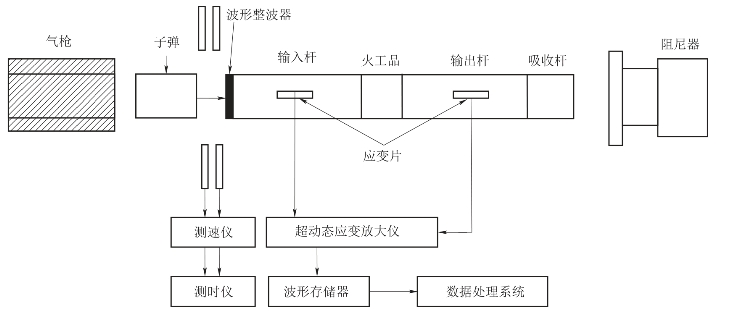
图9.19　SHPB试验装置

9.3.2.2 计算模型

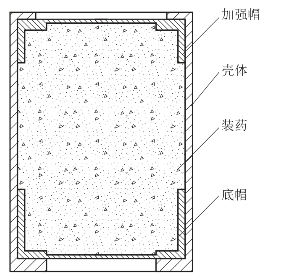
图9.20　针刺雷管的结构

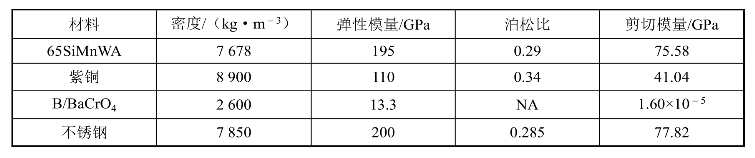
图9.20所示为试验中所采用的雷管结构，其中雷管的壳体材料为不锈钢（1Cr18Ni9Ti），加强帽和底帽为紫铜，装药为B/BaCrO4延期药。图9.21所示为Hopkinson杆简化图，杆材料为65SiMn2WA钢。材料参数如表9.3所示。

图9.21　SHPB的尺寸

表9.3　材料参数

9.3.2.3 材料及本构模型

试验中采用的针刺雷管外壳为不锈钢，加强帽和底帽为紫铜，装药为B/BaCrO4延期药。鉴于模拟火工品动态过载，材料的应变率效应会对结构的响应产生一定的影响，所以不锈钢的本构采用基于Cowper-Symonds应变率的塑性随动模型，紫铜采用Johnson-Cook模型，而B/BaCrO4延期药采用黏弹性模型，Hopkinson杆的变形在弹性范围内，采用线弹性模型。

9.3.2.4 算法及边界条件

由于针刺雷管的尺寸较小，直径和长度一般为几毫米，而分离式Hopkinson杆试验装置的长度总共为2.3 m，模型尺寸相差较大，采用三维模型计算的耗时太长，又因为模型具有轴对称特性，所以采用二维轴对称方法。在仿真计算之前，需要先选择合适的算法，才可能达到正确的结果。研究表明，采用二维ALE算法模拟火工品的变形与试验吻合较好。

LS-DYNA从971R4版本引入二维的流固耦合算法，为解决问题提供了方便。火工品装药采用欧拉算法、其他拉式算法、耦合计算。

图9.22　火工品壳体为拉式算法、其他欧拉算法，1 500 μs时结果

图9.22所示为仿真结果与试验结果的对比，二者变形相差不大，虽然在雷管的输入端有一小部分装药穿透了加强帽，发生了渗漏现象，但通过比较上图的变形与试验结果相差较小，在工程上是可以接受的。图9.23所示为Lagrange算法中的网格重分与流固耦合在同一时刻的比较，二者变形很接近。综合分析，二维ALE算法能保证在合理的计算时间内取得较为理想的结果，所以本书选择二维ALE算法。

(www.xing528.com)

图9.23　320 μs时网格重分（左）和流固耦合（右）的变形图

9.3.2.5 数值模拟结果分析

以撞击杆速度为10.1 m/s时的仿真结果为例，进行分析。由于试验中，Hopkinson杆冲击加载火工品为多次加载，这里将计算时间设为1.5 ms，以保证达到和试验中相同的冲击次数。通过后处理，发现在三次冲击之后，火工品的变形已经很小了，所以取前三次的结果进行比较分析。

选取如图9.24所示的四个典型量来表征针刺雷管在冲击过载下的变形情况，即总长L、输入端直径d1、中间直径d2和输出端直径d3，已知雷管原直径为d0，原总长为L0。

图9.24　针刺雷管四个典型变形量

表9.4　试验与仿真的结果对比

表9.4列出了试验与仿真的数据，为了更直观地分析结果，将结果绘图，如图9.25～图9.28所示。

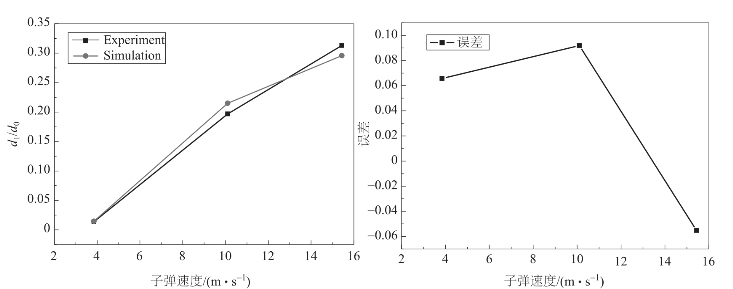
图9.25　试验和仿真输入端直径的相对变形量及误差

图9.26　试验和仿真中间直径的相对变形量

图9.27　试验和仿真输出端直径的相对变形量

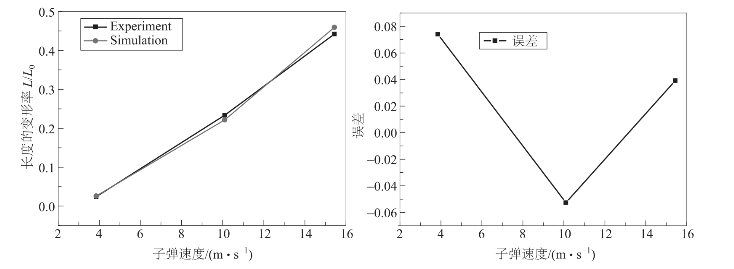
图9.28　试验和仿真总长的相对变形量

以上给出了四个表征量的试验与仿真结果的对比及误差图。其中输入端直径变化、输出端直径变化和总长变化的仿真计算值与试验值的误差相对较小，在10%之内，与试验吻合较好；而雷管中间直径的变形与试验的差距相对较大，最大超过了15%。但是从整体上看，两者符合较好，误差基本在可接受范围之内。

比较不同Hopkinson杆冲击速度下雷管各部分的变形情况。随着冲击速度的增大，雷管轴向发生屈曲压缩，径向发生墩粗，雷管各部分变形量随速度呈线性变化。

比较不同速度下雷管整体结构的变形情况。首先在速度较低时，表征雷管变形的三个直径变化相差不大，是因为速度较低时，试件的应变率较低，加载过程的动力学特征不明显，类似于静力学压缩；而速度较高时，试件的应变率很高，试件在冲击载荷的作用下，出现非均匀变形，输入端（被冲击端）的变形量明显大于输出端（另一端）。

另外需要说明的是，流固耦合算法在低速时，装药和雷管壳体、加强帽及底帽耦合得很好，没有发生流体的渗漏现象；在速度相对较高时，发生了轻微流体渗漏现象，但从试验与仿真结果的对比来看，渗漏对经过的影响很小，可以忽略。